こんにちは(@t_kun_kamakiri)(^^)/
物理を学習しているとどうしても数学の知識というのが欠かせません。
特に物理学では向きを持った値というのを取り扱うために、ベクトル解析というものを勉強しておく必要があります。
しかし、ベクトル解析を勉強していると何やら「高校数学では見たこともない記号:ナブラ演算子\(\nabla\)」があり、それは初学者の興味と恐怖を与えるものです。
前回の記事ではナブラ演算子の基礎を理解する3つのメリットについての記事を書きました。
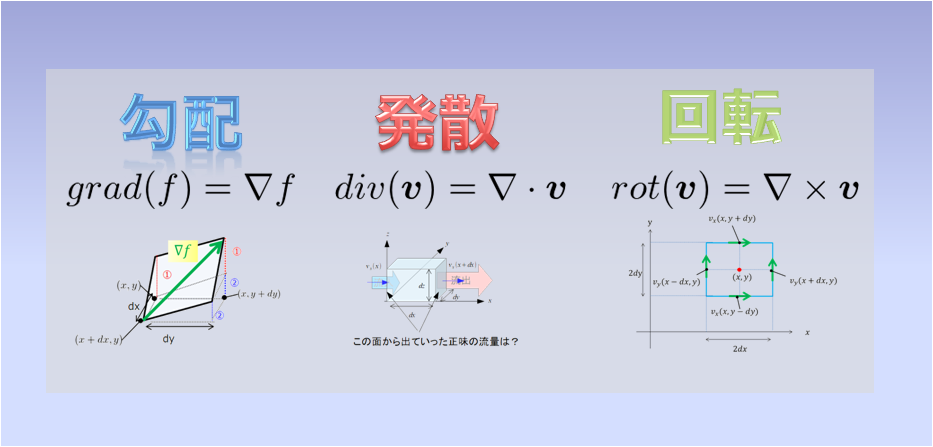
本記事ではナブラ演算子を使ったとても重要な「勾配grad」「発散div」「回転rot」についての解説を行います。
ナブラ演算子を使って以下の内容を解説します。
勾配
\(grad\, f\) or \(\nabla\, f\)
発散
\(div\, \boldsymbol{v}\) or \(\nabla\cdot\boldsymbol{v}\)
回転
\(rot\, \boldsymbol{v}\) or \(\nabla\times\boldsymbol{v}\)
初学者がこれを見て「何だこれは?」とならないためにこの記事を書いています。
- 「\(grad\),\(div\),\(rot\)」に苦手意識がある方
- 「\(grad\),\(div\),\(rot\)」の意味も含めて理解したい方
スカラー場とベクトル場
ナブラ演算子を使った演算を行う前に重要な「スカラー場」と「ベクトル場」について簡単に解説をしておきます。
なぜ、「スカラー場」と「ベクトル場」について解説が必要かというと以後の内容でナブラ演算子を作用させた結果はスカラー場なのかベクトル場なのかによって物理的な意味合いが変わってくるからです。
スカラー場
スカラー場は、空間の各点に対して数値(スカラー量)が与えられている状態のことです。
例えば、以下のような2次元平面での温度分布がスカラー場に当たります。
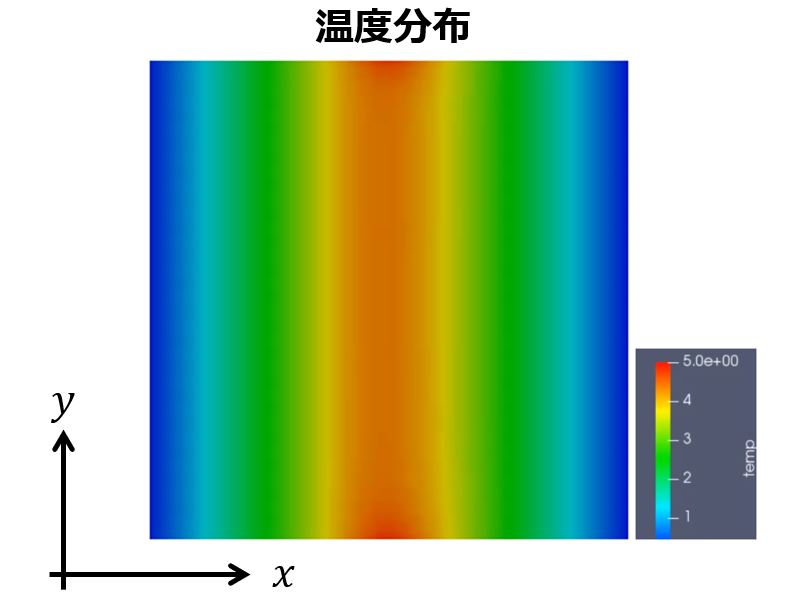

空間座標$(x,y)$に対して温度は$T(x,y)$のような関数で表すことができます。
このように$(x,y)$に対してただ一つの値を持つものがスカラー場です。
その他の例
- 圧力
- 密度
もスカラー場になります。
同様に3次元空間を考えると$(x,y,z)$に対してただ一つの値を持つものがスカラー場で、温度を例に取ると$T(x,y,z)$のように書きます。
ベクトル場
ベクトル場は、空間の各点に対してベクトル量が与えられている状態のことです。
ベクトルとは「向き」と「大きさ」を持った量です。


例えば、以下のような2次元平面での流速ベクトル分布がベクトル場に当たります。
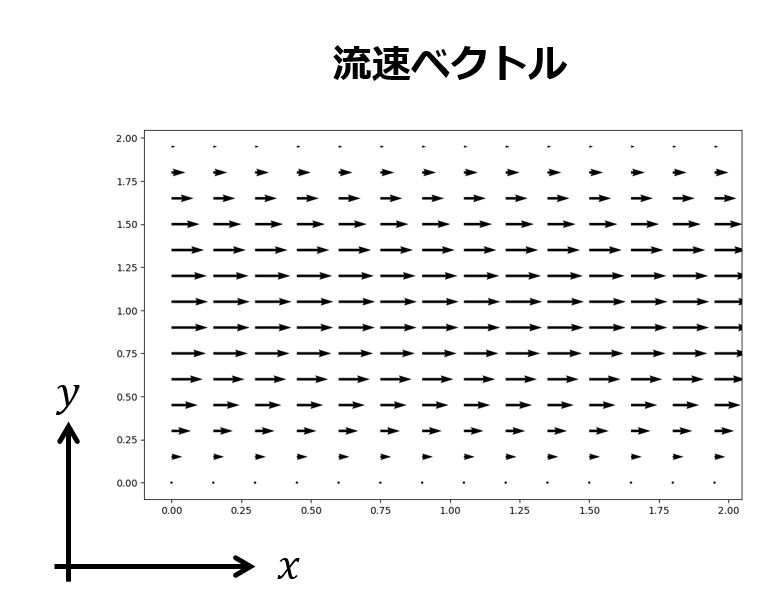


空間座標$(x,y)$に対して流速は$\bm{v}=(v_{x}(x,y),v_{y}(x,y))$のようにベクトルの$x$成分、$y$成分は各点の関数で表すことができます。
同様に3次元空間を考えると$(x,y,z)$に対してベクトル場は$\bm{v}=(v_{x}(x,y,z),v_{y}(x,y,z),v_{z}(x,y,z))$のように書きます。
ナブラ演算子って何?
ナブラ演算子(\(\nabla\))ってそもそも何かってことをちょびっと話しておかないと、「そこがわからんのだ」って思われそうなので、最初に話しておきたいと思います。
- \(\nabla\):「ナブラ」と呼びます。
- \(\nabla=(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z})\)
※\(x,y,z\)が変数
とても簡単にまとめると以上です。
要するに、\(\nabla\)演算子は「誰かを偏微分したくてたまらないやつ」とくらいに思っておきましょう。
■例えば、\(f(x,y,z)=2x^{2}+y^{3}+z\)という$x,y$を変数に持った関数を用意します。この関数に左から「誰かを偏微分したくてたまらない演算子(\(\nabla\)演算子)を作用させることを考えます。
とても素直に計算するだけです。
&=\bigg(\frac{\partial f(x,y)}{\partial x},\frac{\partial f(x,y)}{\partial y},\frac{\partial f(x,y)}{\partial z}\bigg)\\
&=\big(4x,3y^{2},1\big)\end{align*}
素直に計算してみただけです。
スカラー場の関数$f(x,y)$にナブラ演算子を作用させるた結果がベクトル場になりましたね。
■もうひとつ例を見てみましょう。
例えば、あるベクトル場\(\boldsymbol{v}(x,y)=(v_{x},v_{y},v_{z})=(2x^{2},y^{3},z)\)に「誰かを偏微分したくてたまらない演算子(\(\nabla\)演算子)を作用させること考えます。
今度は内積の形で作用させます。
&=4x+3y^{2}+\end{align*}
となります。
ベクトル場の$\bm{v}(x,y)$にナブラ演算子の内積を作用させるた結果がスカラー場になりましたね。
まずは素直に「\(\nabla\)演算子を使うとまるでベクトルで学習した内容っぽく計算できるな」って感じて慣れていけばよいのかと思います。
しかし、物理数学のベクトル解析でナブラ演算子を勉強すると「\(grad\),\(div\),\(rot\)」も一緒に習うことになります。
ここではもう少しナブラ演算子を使った単なる演算子の計算にとどまらない意味を持った操作であることを説明したいと思います。
勾配:gradient
まずはナブラ演算子を使った簡単な例は「勾配」です。
なぜ\(grad\)と書くのかというと勾配の英語がgradientだからその冒頭3文字を使って\(grad\)と書くのです。
「勾配」に関する書き方は、\(grad \,f\)だったり\(\nabla f\)だったりしますが、ある関数\(f\)に\(\nabla\)演算子を作用させる操作によってできます。
こんな感じで書きます。
簡単な例で見てみましょう。
これを見れば、\(\nabla\)演算子をある関数\(f\)に作用させる操作が「勾配」であることがわかるかと思います。
2変数\(z=f(x,y)\)の場合
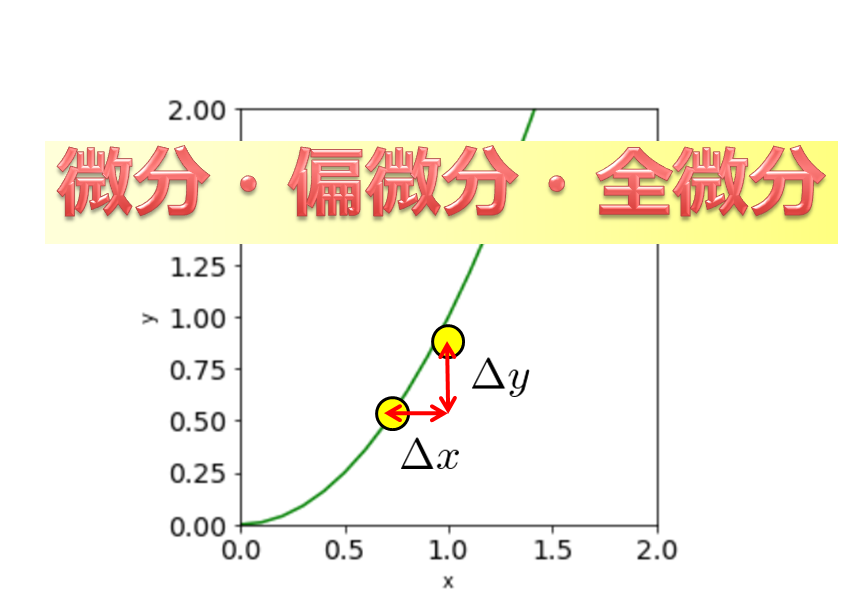
2変数\((x,y)\)の場合の全微分を考えましょう。
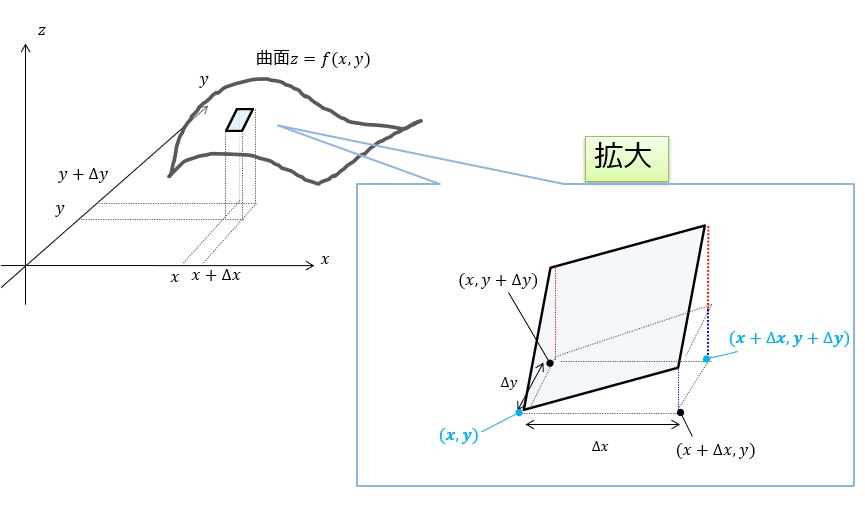

ここで$(x,y)$平面上で$(x,y)$から$(x+\Delta x,y+\Delta y)$へ変化したときに高さ方向の$\Delta f = f(x+\Delta x,x+\Delta y)-f(x,y)$はどのように書けるかを考えます。
絵で描くとこんな感じ。
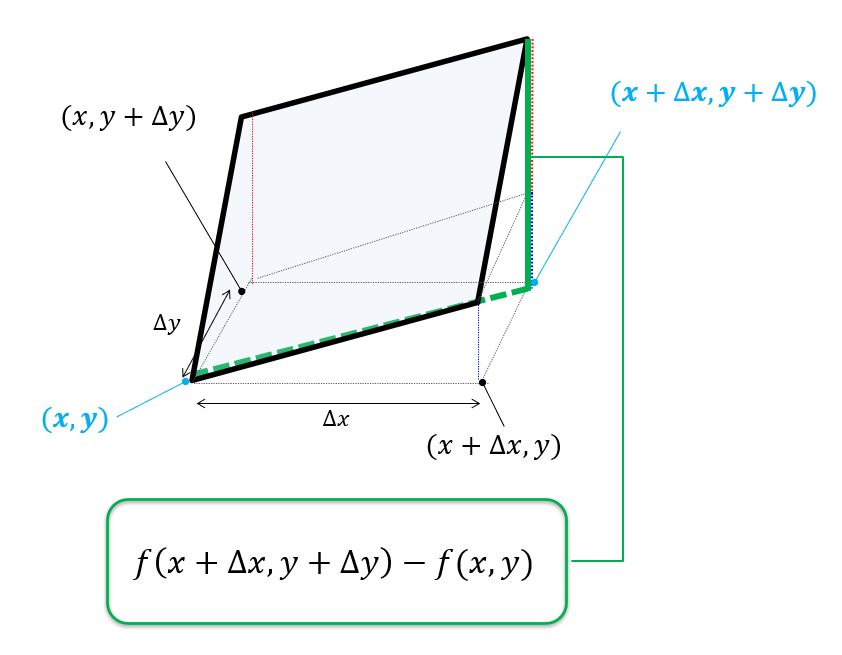

これをひとつひとつ考えてみます。
■まず、$y$方向を止めて$x$方向だけの変化を考えます。
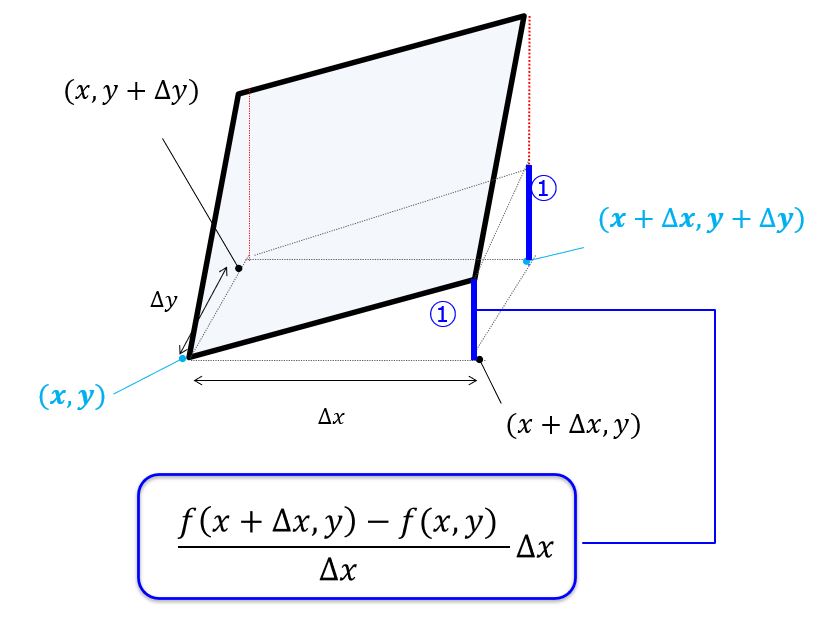

\frac{f(x+\Delta x,y)-f(x,y)}{\Delta x}\Delta x\underset{\Delta x\rightarrow 0}{\underline{\rightarrow }}=\frac{\partial f}{\partial x}dx
\end{align*}
となります。
※$\frac{\partial f}{\partial x}$は$y$を固定して$x$でのみ微分を行うことを意味します($x$による偏微分)
■次に、$x$方向を止めて$y$方向だけの変化を考えます。
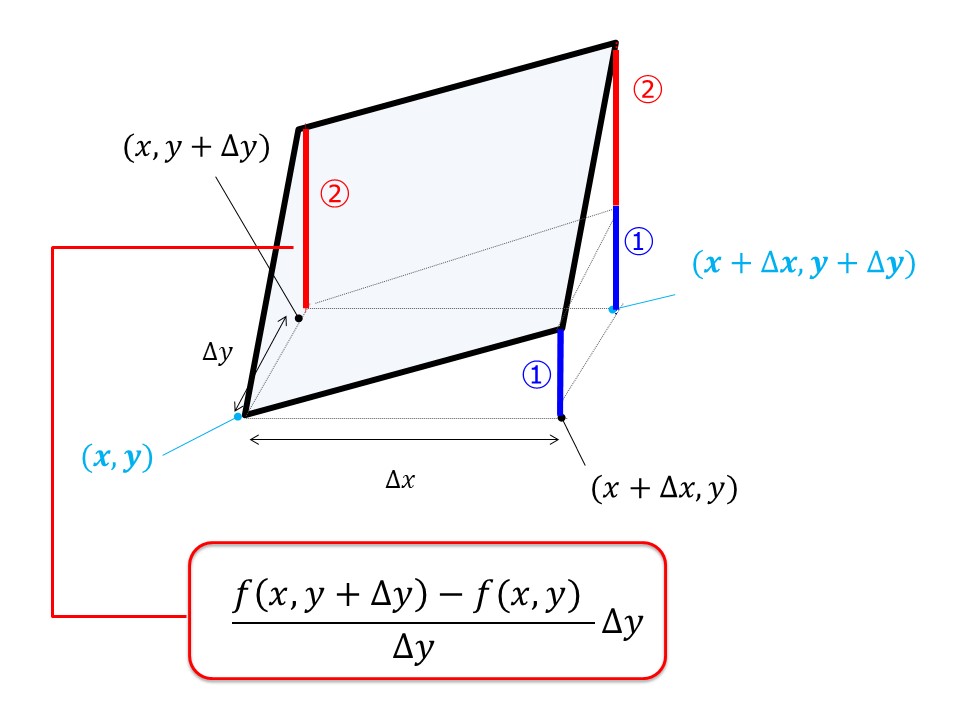

\frac{f(x,y+\Delta y)-f(x,y)}{\Delta y}\Delta y\underset{\Delta y\rightarrow 0}{\underline{\rightarrow }}=\frac{\partial f}{\partial y}dy
\end{align*}
となります。
※$\frac{\partial f}{\partial y}$は$x$を固定して$y$でのみ微分を行うことを意味します($x$による偏微分)
以上より$\Delta f = f(x+\Delta x,y+\Delta y)-f(x,y)$は①+②であることがわかります。
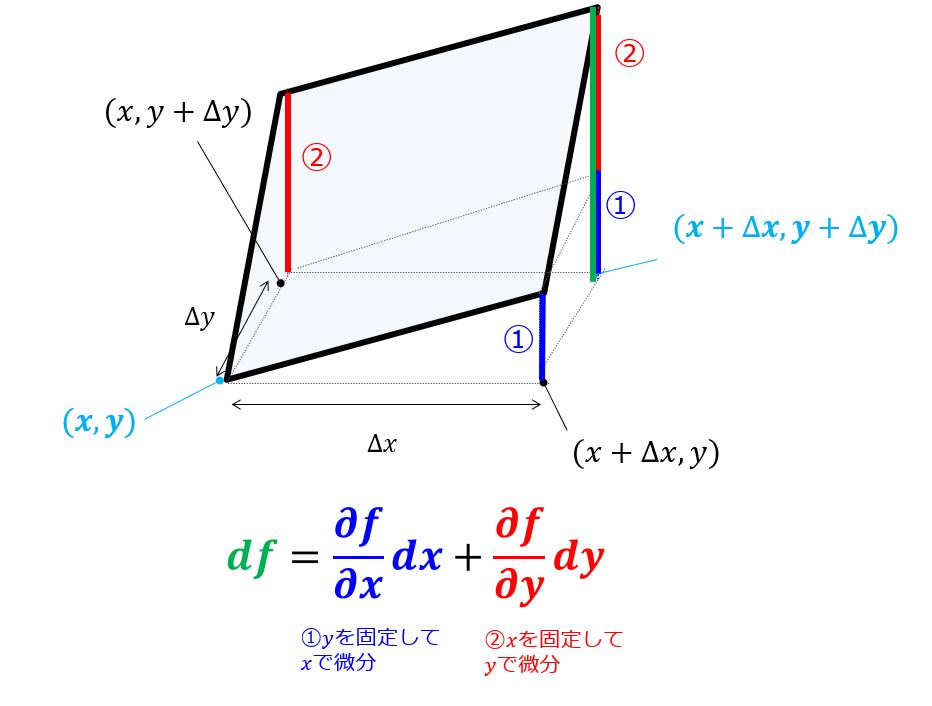

全微分は上の表式になります。
df=\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy
\end{align*}
これをこのように各成分に分解して内積の形で書くと、
df=\bigg(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\bigg)\cdot (dx,dy)\end{align*}
となります。
おっと、「\(\big(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\big)\)が出てきたではありませんか」ということになります。
これを、
&=\bigg(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\bigg)\end{align*}
と書いて勾配を表すのです。
では、なぜ勾配と呼ぶのか・・・・wikipediaには「勾配;gradient」について、
このように書いています。
スカラー場の変化率が最大となる方向への変化率と書いてあります。
というわけで\(\nabla f\)を勾配という意味がわかるように\(grad f\)の意味を考えてみます。
等高線に対して垂直な方向が\(\nabla f\)の方向
先ほど書いた式が内積の形で書くことができたので、以下のように書きましょう。
df=\left | grad\,f \right |\left | \Delta \bm{r} \right |\cos\theta \end{align*}
※$x,y$平面上の微小変化を$\Delta \bm{r}= (dx,dy)$と書きました。
※$grad\,f$と$\Delta \bm{r}$のなす角度を$\theta$としています。
「等高線に対して垂直な方向が\(\nabla\,f\)の方向」とはどういう意味か考えてみましょう。
等高線を描いて考えてみます。
$\Delta \bm{r}$の動かし方を次の2通りの場合で考えてみます。
- $\Delta \bm{r}$を等高線の方向に動かす場合
- $\Delta \bm{r}$を$df$が最大になるように動かす場合
■$\Delta \bm{r}$を等高線の方向に動かす場合について
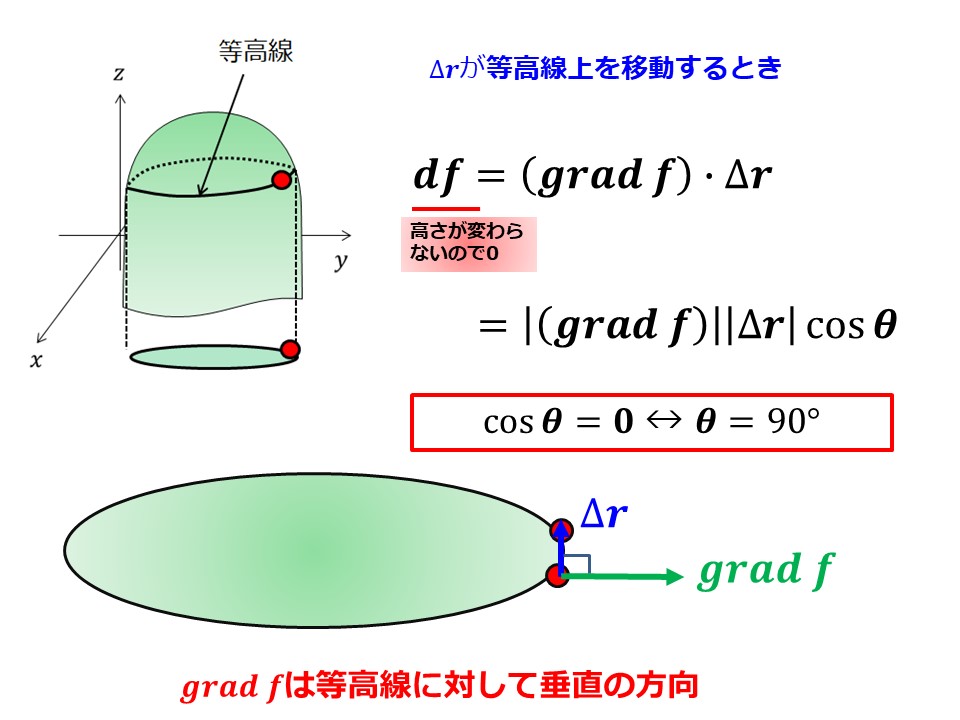

$\Delta \bm{r}$を等高線の方向に動かすと、$df$の高さが変わらないため$df=0$となります。
なので、内積の定義から$\theta=90$となり、$grad\,f$と$\Delta \bm{r}$は直交していることがわかります。
つまり、$grad\,f$は等高線対して垂直であることがわかります。
■$\Delta \bm{r}$を$df$が最大になるように動かす場合
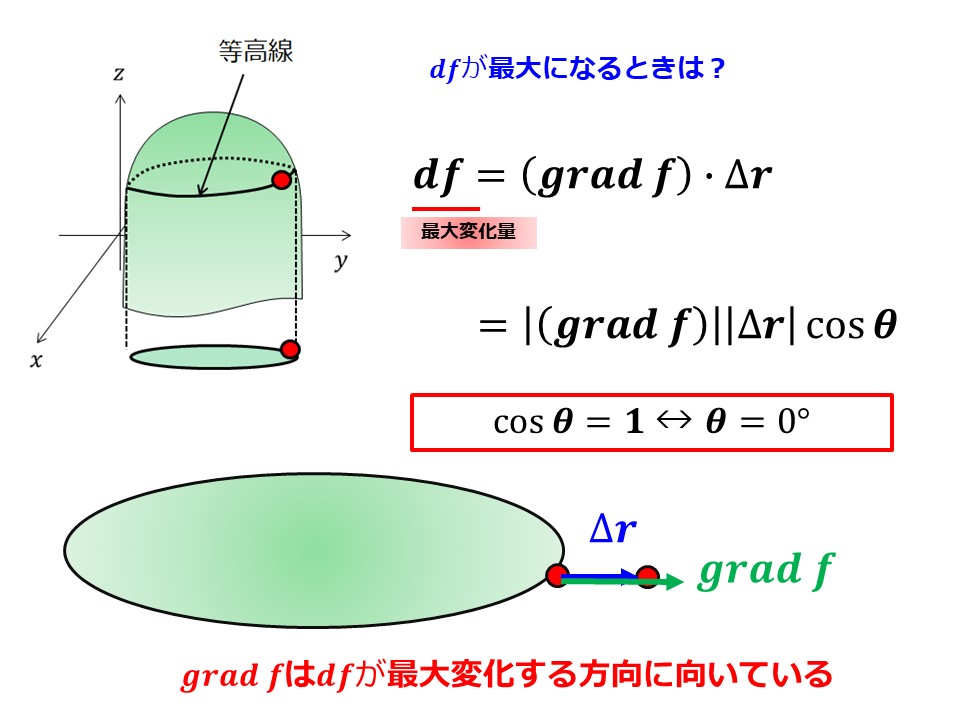

$\Delta \bm{r}$を$df$が最大になる方向に動かした場合、内積の定義から$\theta=0$となり、$grad\,f$と$\Delta \bm{r}$が同じ方向を向いていることがわかります。
つまり、$grad\,f$は$df$が最大になる方向を向いているがわかります。
ゆえに、$grad\,f$はスカラー場の変化率が最大となる方向と説明できるわけです。
では、3変数だったら?
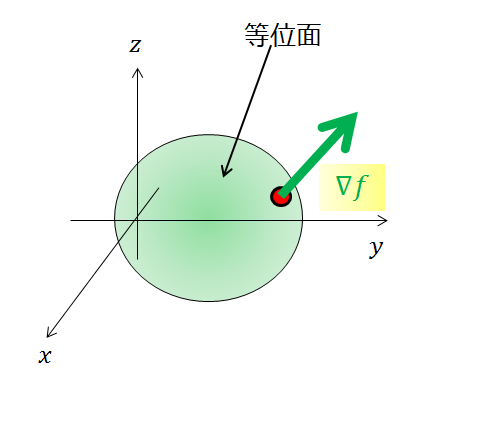
3変数\(w=f(x,y,z)\)の場合
3変数になる表現するための軸が足りないので\(w\)の大きさは色とかで区別するしかないです。
先ほど「2変数で等高線(\(z=f(x,y)\)の値が常に同じ)」を考えたように、「3変数で等位面(\(w=f(x,y,z)\)の値が常に同じ)」場合での\(\nabla \,f\)の方向を考えることができます。
3変数での等位面での\(\nabla f\)の方向は、等位面に対して垂直な方向です。

ここまで抑えておけば基本的なことはOKです!
発散:divergence
数学記号での発散の表現は\(div\)か\(\nabla\cdot\)となります。
\(\nabla\)演算子とあるベクトル場\(\boldsymbol{v}\)との内積であると覚えておきましょう。
なぜ\(div\)と書くのかというと発散の英語がdivergenceだからその冒頭3文字を使って\(div\)と書くのです。
また、\(\nabla=(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z})\)を使って、あるベクトルとの内積をとるとそれは発散を意味することになります。
と書きます。
ナブラ演算子の部分について、「記号を使っていてはわからない」って方は、実際に内積を計算してやると、
となることを覚えておけば良いでしょう。
しかし、数学記号で発散と言われてもピンとこないのがふつうであると思います。
まずは簡単にイメージを頭にインプットするために、あるベクトル場を流速ベクトル\(\boldsymbol{v}\)として川の流れを考えて、「発散」について理解していきたいと思います。
発散がない場合
発散がない場合という、「発散」という言葉を使うとよくわからないことでしょうね。
発散がない場合というのは、「発散=出ていった量(流出)ー入ってきた量(流入)」は0という場合を意味しています。
大事なのは、発散は正味に出ていった量ということです。
流量は出ていくんですけど、入ってくる量も合わせて、「実際どれだけ出ていったのか?」が発散の意味です。


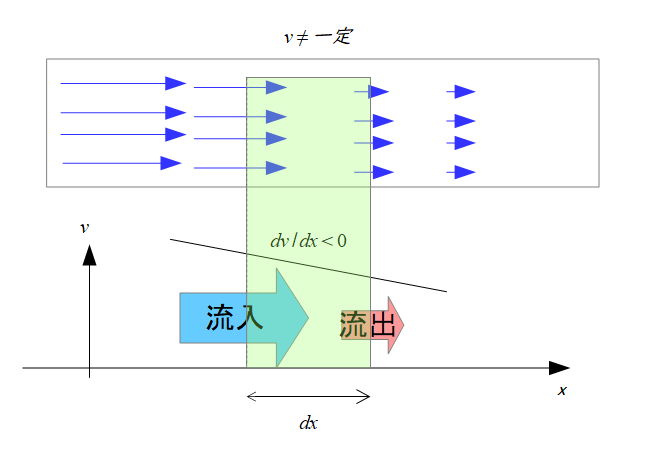
例えば上の絵のように1次元の流速が一定の流れがある場合を考えます。
この場合は、緑の半透明に入ってきた水の量と出ていった水の量は同じですよね。
だから、「発散=出ていった量(流出)ー入ってきた量(流入)」は0ということになります。
発散記号で書くと、
です。
ナブラ演算子を用いると、
です。
これをナブラ演算子で使わずに記述すると、
です。
実際、流れは一定なのですから、
であります。
発散がある場合
発散がある場合というのは、「発散=出ていった量(流出)ー入ってきた量(流入)」は0ではないということを意味しています。
流入してきた量に対して「湧き出し」もしくは「吸い込み」があるということです。
湧き出し
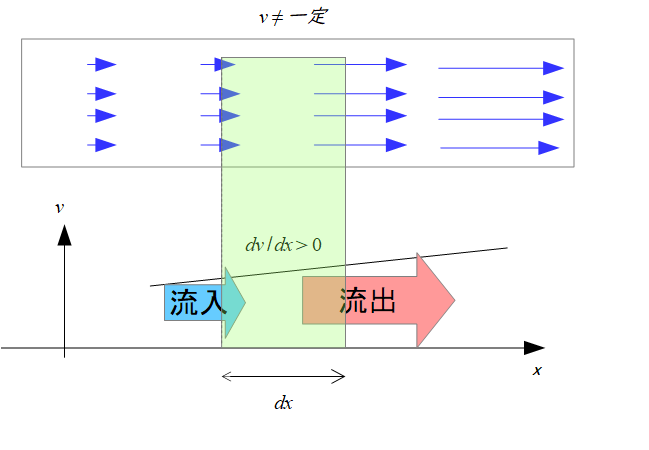

上の絵のように右にいくほど(\(x\)の増加とともに)流速が増えていっている場合の流れでは、緑の透明に入ってきた水の量より出ていく水の量の方が多いので、正味の出ていった量というのは0より大きいです。
これを湧き出しと言います。
です。
ナブラ演算子を用いると、
吸い込み
湧き出しの逆の吸い込みの場合を考えましょう。

緑の透明に入ってきた水の量流入してきた量に対して出ていく水の量の方が多少ない場合は正味の出ていった量というのは0より小さくなります。
これを吸い込みと言います。
です。
ナブラ演算子を用いると、
なぜ\(\nabla\)演算子との内積が発散なのかを導出する
ではなぜ\(\nabla\)演算子の内積が発散を意味しているのかを考えたいと思います。
「$x,y,z$方向に垂直な面から出ていく正味の流量」を考えることで発散を理解したいと思います。
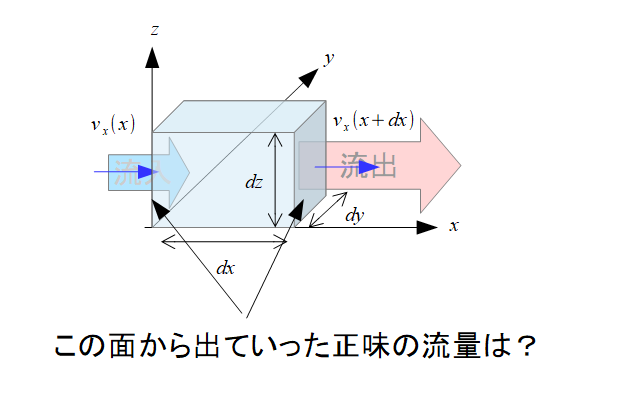

さて、右の面から出ていく流量と左の面から入ってくる流量というのを考えます。
- 出ていく流量:\(v_{x}(x+dx)dydz\)
- 入ってくる流量:\(v_{x}(x)dydz\)
※\(dx,dy,dz\)は微小量としています。
すると正味の出ていく流量は、
ということになります。
これをもう少し式変形してみましょう。
&=\frac{v_{x}(x+dx)-v_{x}(x)}{dx}dxdydz\end{align*}
ここで\(dx→0\)とすると、\(\frac{v_{x}(x+dx)-v_{x}(x)}{dx}=\frac{dv_{x}}{dx}\)だから、
「x方向に垂直な面から出ていく正味の流量」
となります。
同様の手順を「\(y\)方向に垂直な面」「\(z\)方向に垂直な面」の正味の出ていった量を加えれば良いだけです。
もう一度式変形をするまでもなく、
「y方向に垂直な面から出ていく正味の流量」
「z方向に垂直な面から出ていく正味の流量」
これらを足すと、
となります。
今考えている直方体は任意な大きさにしていました(とりあえずとても小さいと考えていました)ので、単位体積あたりに出ていった正味の流量は、
ということになります。
これで発散を数式で表現することができました。
よく見ると\(\nabla\)演算子との内積になっているのがわかりますね。
回転:rotation
数学記号での回転の表現は\(rot\)か\(\nabla\times\)となります。
\(\nabla\)演算子とあるベクトル場\(\boldsymbol{v}\)との外積であると覚えておきましょう。
なぜ\(rot\)と書くのかというと回転の英語がrotationだからその冒頭3文字を使って\(rot\)と書くのです。
また、\(\nabla=(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z})\)を使って、あるベクトルとの外積をとるとそれは回転を意味することになります。
と書きます。
これを成分ごとに書いてみます。
\begin{pmatrix}
\frac{\partial }{\partial x}\\
\frac{\partial }{\partial y}\\
\frac{\partial }{\partial z}\\
\end{pmatrix}\times
\begin{pmatrix}
v_{x}\\
v_{y}\\
v_{z}\\
\end{pmatrix}
=
\begin{pmatrix}
\frac{\partial v_{z}}{\partial y}-\frac{\partial v_{y}}{\partial z}\\
\frac{\partial v_{x}}{\partial z}-\frac{\partial v_{z}}{\partial x}\\
\frac{\partial v_{y}}{\partial x}-\frac{\partial v_{x}}{\partial y}\\
\end{pmatrix}
\end{align*}
↑このようになります。
見ての通り、\(grad\)や\(div\)と比較するとめちゃ覚えにくいです。
ですので覚え方を自分なりに持っておく必要があります。
ここでは、2通りの覚え方を紹介しますので覚えやすい方を自分なりに選んで覚えておきましょう。
3行3列の行列式から「サラスの公式」を使う
もし線形代数を既に履修済みで「サラスの公式を知っているよ」って方でしたら覚えやすい方法だと思います。
\begin{vmatrix}
\boldsymbol{i} & \boldsymbol{j} &\boldsymbol{k} \\
\frac{\partial }{\partial x} & \frac{\partial }{\partial y} & \frac{\partial }{\partial z}\\
v_{x} & v_{y} & v_{z}
\end{vmatrix}
\end{align*}
このように3行3列の行列式を用意します。
ここで、\(\boldsymbol{i}\)、\(\boldsymbol{j}\)、\(\boldsymbol{k}\)はそれぞれ\(x\)、\(y\)、\(z\)方向の単位ベクトルを表しています。
「サラスの公式」は3行3列の行列式を計算するときにの公式ですが、公式通りに従えば\(\nabla\)演算子の外積を計算していることになります。
では、「サラスの公式」通りに計算してみます。
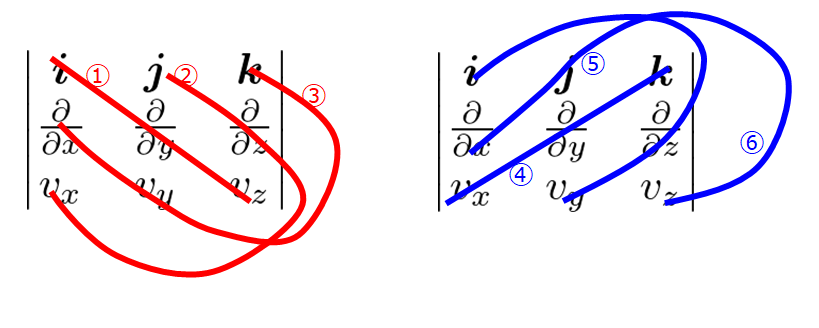
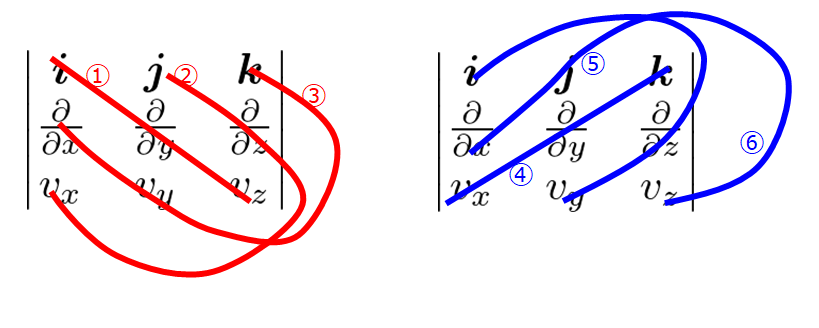
(①+②+③)–(④+⑤+⑥)を計算すれば良いです。
\end{align*}
これをもう少しまとめると、
と、このようになります。
各成分を見ると確かに\(\nabla\)演算子との外積の結果と同じですね。
僕は、この方法ではなくて次の方法で\(\nabla\)演算子との外積を覚えています。
\(\nabla\)演算子との外積というよりは、外積の計算そのものであるため、ベクトルの外積計算にも使うことができます
「クロスして」「それ以外の成分に書く」
「クロスして」「それ以外の成分に書く」・・・と呪文のように覚えているこの方法は、結構良いかなと思っています。
誰に習ったのかは忘れましたが。
手順はこんな感じです。
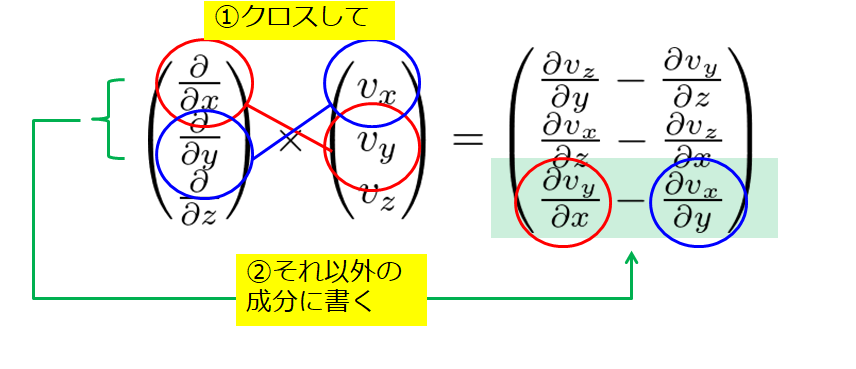

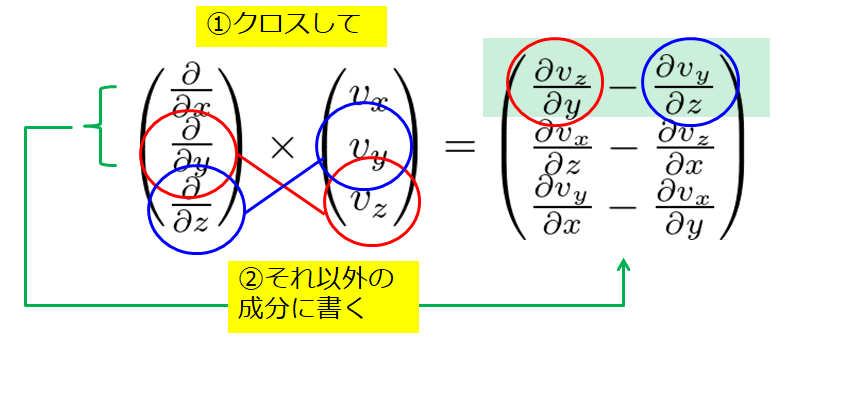

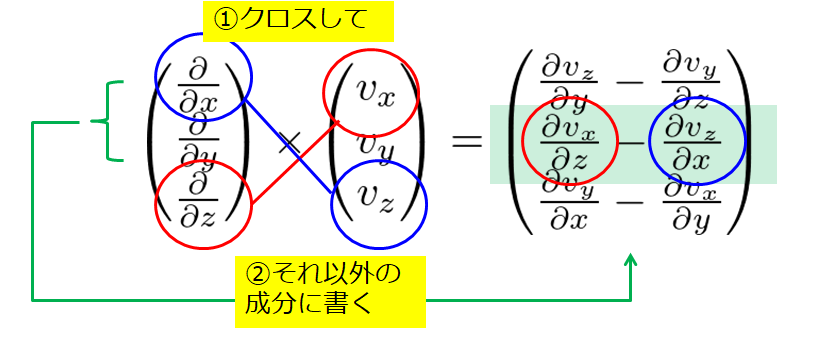

言葉で書くよりも絵を使った方がわかりやすいので絵で表現してみました。
どうですかね。
結構覚えやすいと思うのですがね。
なぜ\(\nabla\)演算子との外積が回転なのかを導出する
さて、\(\nabla\)演算子の外積の形式はわかりましたが、回転(\(rot\))と表現される所以を理解する必要があります。
発散の場合は、「ある微小体積を出入りした量」でしたよね。
回転の場合は、「ある微小領域まわりのモーメント」を考えれば良いのです。
モーメントなので回転ってことです。
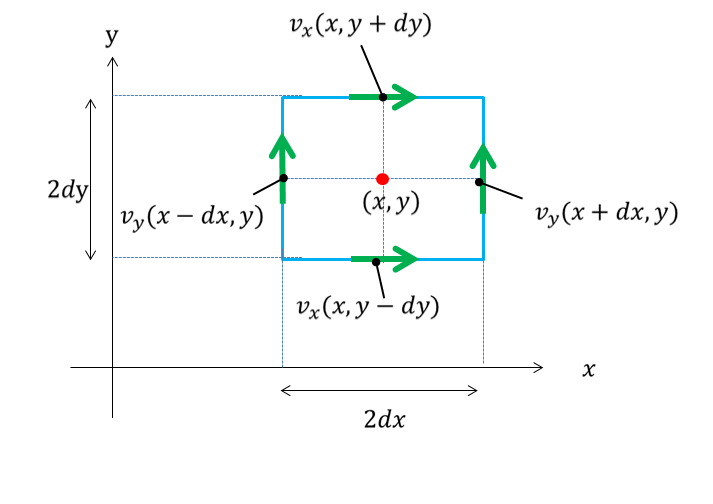

簡単のために2次元にして、上の絵のようにある点\((x,y)\)まわりのモーメントを考えてみましょう。
※\(2dx=2dy=2da\)の微小領域での\(z\)軸方向まわりのモーメントを考えます。
反時計回りを正方向にして・・・・
&v_{y}(x+dx,y)dx+v_{x}(x,y-dy)dy-v_{x}(x,y+dy)dy-v_{y}(x-dx,y)dx\\
&=\frac{v_{y}(x+dx,y)-v_{y}(x-dx,y)}{2dx}2dx\,dy-\frac{v_{x}(x,y+dy)-v_{x}(x,y-dy)}{2dy}2dx\, dy\\
&=\big(\frac{\partial v_{y}}{\partial x}-\frac{\partial v_{x}}{\partial y}\big)2da^2\end{align*}
となります。
としておくと、微小領域\(4dx\,dy=4da^2\)は任意に選んだ領域ですので、単位面積あたりのモーメントは、
となります。
\(\frac{1}{2}\)がついてしまっていますが、本質的にはこれは\(z\)軸まわりの回転を意味しています。
\(z\)軸まわりの回転は、
となるので、rotの結果は$z$軸まわりの回転に相当する量であることがわかります。
これを\(x\)軸まわりと\(y\)軸まわりモーメント(回転)を考えると、3軸での回転を考えることができるというわけです。
まとめ
これで\(\nabla\)演算子を使った「勾配:\(grad\)」「発散:\(div\)」「回転:\(rot\)」の意味がわかったでしょうか。
今一度全体をまとめておきます。
本記事の内容をpdf化してみました。
pdf化にあたって再度書き直した部分があるため、細かなミスがあるかもしれません。
おすすめの参考書
最後におすすめの参考書を紹介しておきましょう。
マセマの参考書は大学初学年や、なんだったら高校生でも読めるくらいわかりやすく書かれていますので、「大学数学はキツイな」って感じた方は手に取ってみてください。























I think that what you published was actually very logical.
But, think on this, what if you added a little content?
I mean, I don’t wish to tell you how to run your blog, but what if you
added something that makes people want more? I mean 初学者のためのナブラ演算子を用いた「勾配grad」「発散div」「回転rot」|宇宙に入ったカマキリ is kinda
boring. You could look at Yahoo’s home page and note how they create article titles to grab viewers to click.
You might add a related video or a pic or two to get readers interested about everything’ve got to say.
Just my opinion, it could bring your posts a little bit more interesting.
My page :: how much does cialis cost
初めまして、高校で物理の非常勤をしています酒井と申します。高校では電磁波についてマクスウェル方程式は名前程度で内容は扱いませんが興味を持つ生徒もいるのではと思っています。その準備としてここでのベクトル解析の基礎が必要と思いネット検索しましたが本HPが非常に分かりやすく解説されていました。そこで2,3お尋ねしたいことがあります。
1.生徒向けのプリントを作りたいのですがHP内の図などを使用してもいいでしょうか。(出典を明記の上)
2.gradの説明のところで
f(x+Δx,y)-f(x,y)=δf/δx・Δxをテイラー展開のΔの2次以上の項を無視するという解釈ではいけませんか。
以上ご回答いただければ幸いです。
ブログをお読みいただきありがとうございます。
1.図の使用に関しては構いませんので、お使いいただければと思います。
ただし、図の間違いも含む可能性がありますので、それによるトラブルは責任を負いかねますのでご了承ください。
その際はお手数おかけしますが、ご連絡いただけますと幸いです。
2.「f(x+Δx,y)-f(x,y)=δf/δx・Δxをテイラー展開のΔの2次以上の項を無視するという解釈ではいけませんか。」でも良いと思います。
簡単に説明しますと、f(x+Δx,y)-f(x,y)=∂f/∂x・ΔxはΔx→0としたときの微分の定義式に従っているという考えですが、f(x+Δx,y)をテーラー展開してΔx,Δx^2,Δx^3…によるテーラー展開は項はf(x)の広い領域での近似式ですが、
Δx→0にするとΔx^2,Δx^3などの高次の項は無視でき、f(x+Δx,y)-f(x,y)=∂f/∂x・Δxに帰着します。
よろしくお願いいたします。
丁寧なご回答ありがとうございました。このあたりの内容は大学1年次の物理か数学で出てくると思いますが自分自身けっこうつまずいた経験があるので高校のときに少しでも慣れておくことは無駄ではないように思い教材として考えてみました。マクスウェル方程式の他ケプラーの3法則で
楕円軌道になること(極座標表示と微積分の利用)や空気中での音速の式、断熱変化でのポアソンの式などの教材化も考えています。今回はありがとうございました。