こんにちは(@t_kun_kamakiri)(‘◇’)ゞ
最近、モデリカのためのオープンソースであるOpenModelicaとか使って遊んでいます。
本記事の本筋は以下の内容です。
OpenModelicaを使って・・・
のモデル作りから計算までを体験してみましょう(^^)/
運動方程式
OpenModelicaについては前の記事でちょろっと説明しました。
※OpenModelicaのバージョンは、「1.13.2 (64-bit)」を使っています。
バネの振動をOpenModelicaで体験してみよう
バネの振動における理論を説明した後、
OpenModelicaを使ってバネの振動の解析をしたいと思います(^^)/
バネの振動の理論は?
バネの運動は、とても簡単な方程式で記述できます。
バネの振動の運動方程式
と、このように書くことができます。
- バネ定数:\(k=10\)[N/m]
- 質量:\(m=10\)[kg]
とします。
このような微分方程式には解析解が存在するので、わざわざシミュレーションをする必要もないですが、OpenModelicaの結果と比較して理解するために理論の面も押さえておきます。
2階の微分方程式なので、解析解も以下のように求めることができます。
(1)の一般解
ここで、固有振動数\(\omega=\sqrt{\frac{k}{m}}\)とおきました。
2回の微分方程式なので、(1)から求めた\(x\)では「積分定数(\(A,B\))」が2つあります。
この「積分定数」は、初期条件を定めることで決定されます。
初期条件を以下のように決めます。
- 質点の初期位置:\(x_{0}=0[m]\)
- 質点の初速度:\(v_{0}=10[m/s]\)
そうすると、以下のように解が定まります。
※(2)式から初期条件を定めて得られた解なので、特殊解と呼ばれています。
(2)の特殊解
こんな感じで(1)の解析解がわかっているのでCAE解析をする必要はないのですが、OpenModelicaを体験するには最も簡単なモデルなのではないかと思います。
次に、OpenModelicaを使って「バネの振動」を解きたいと思います。
バネの振動をOpenModelicaでモデル作成
では、OpenModlicaを使ってバネのモデル構築をしてみましょう。
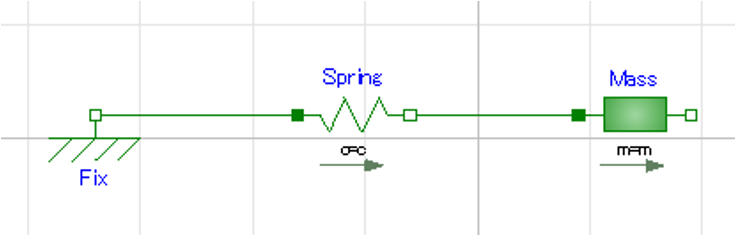

操作方法は以下の動画を参考にしてください。
OpenModelicaで得られた解と理論解(3)式とを比較
OpenModelicaの結果を「csvファイル」として出力ができるので、csvファイルにして理論解の波形と重ねてみます。
OpenModelicaのcsvファイル出力
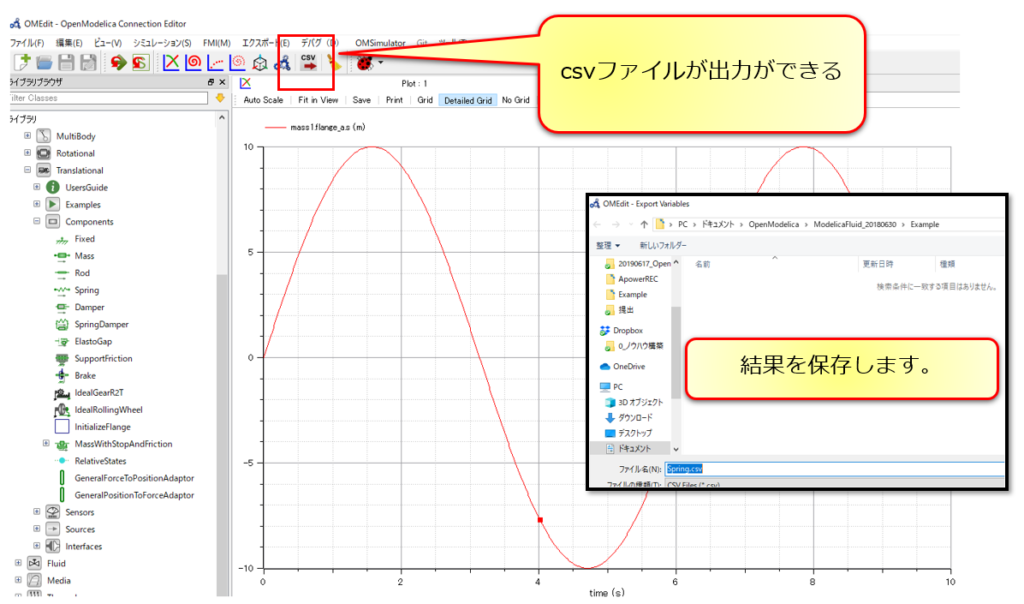

OpenModelicaで得られた解と理論解(3)式の比較
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
import numpy as np from scipy.integrate import odeint import matplotlib.pyplot as plt #理論解 m = 10 # 質量[kg] k = 10 # 剛性[N/m] state0 = [0.0, 10.0] # 初期値[x0, v0] omega = np.sqrt(k/m) #固有角振動数 t0 = 0 # 初期時間[s] tf = 10 # 終了時間[s] dt = 0.005 # 時間刻み[s] t = np.arange(t0, tf+dt, dt) # 時間軸配列 x_thory = (state0[1]/omega * np.sin(omega * t)) +\ (state0[0] * np.cos(omega * t)) #配列要素として読み込む array=np.genfromtxt('./Spring.csv',delimiter=',',dtype=float,skip_header=2) array_t=np.transpose(array) #リスト型に変換 time_ana=list(array_t[0]) x_ana=list(array_t[1]) #グラフの作成 plt.plot(time_ana,x_ana,label="OpenModelica") plt.plot(t,x_thory,label="theory") ##フォントサイズの指定 plt.xticks(fontsize=7) plt.yticks(fontsize=7) ##グリッドの有無 plt.grid(True) ##x軸とy軸のラベル plt.xlabel("time[sec]") plt.ylabel("x[m]") #凡例の位置 plt.legend(loc='best') ##グラフを描く plt.show() |
グラフの比較


一致しているので、グラフが重なっています(^^)/