【OpenModelica入門】シンプルな熱回路網の解説

こんにちは（@t_kun_kamakiri）

最近、モデリカのためのオープンソースであるOpenModelicaのお勉強中です。
正確には流体解析のOpenFOAMとOpenModelicaとの連携をしたい思いがあり、OpenModelicaの勉強を再開したというのが同期になります。

モデルベース小委員会ハンズオンセミナーに参加

「本記事を書こう + 勉強しよう」と思ったは、2025年3月28日（金）14:30～16:30にこちらの無料セミナーを受講したことがきっかけです。

熱回路網のモデリング手法を解説していただき、非常によく理解できたと思っています。
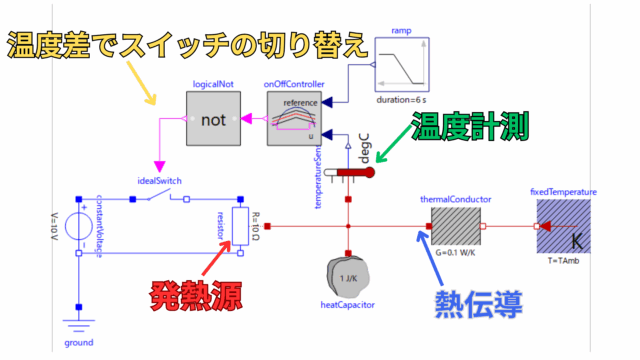
最終的に作成するのは以下のモデルです。
何のことかわからないかもしれませんが…

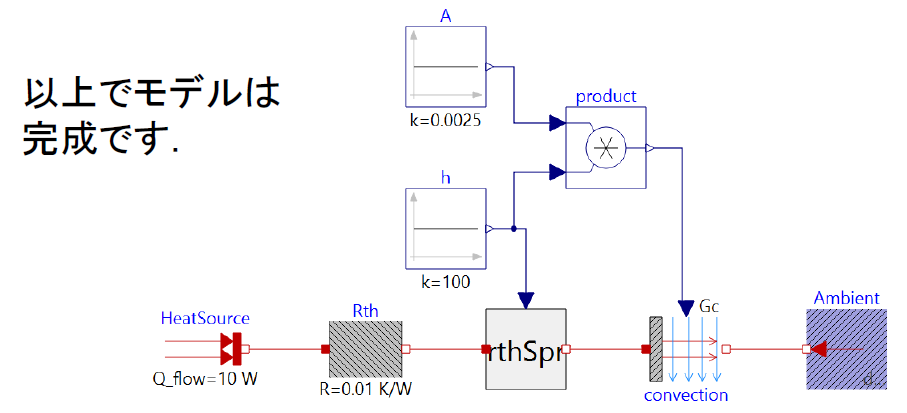
初級者から少し中級者への架け橋になる感じのセミナーだったものを会員・非会員問わず無料で開催していただき非常に満足です。

というわけでもう少し簡単なモデルを使って自分でも理解したことを本記事でまとめていこうと思います。

シンプルな熱回路網（熱伝達あり）

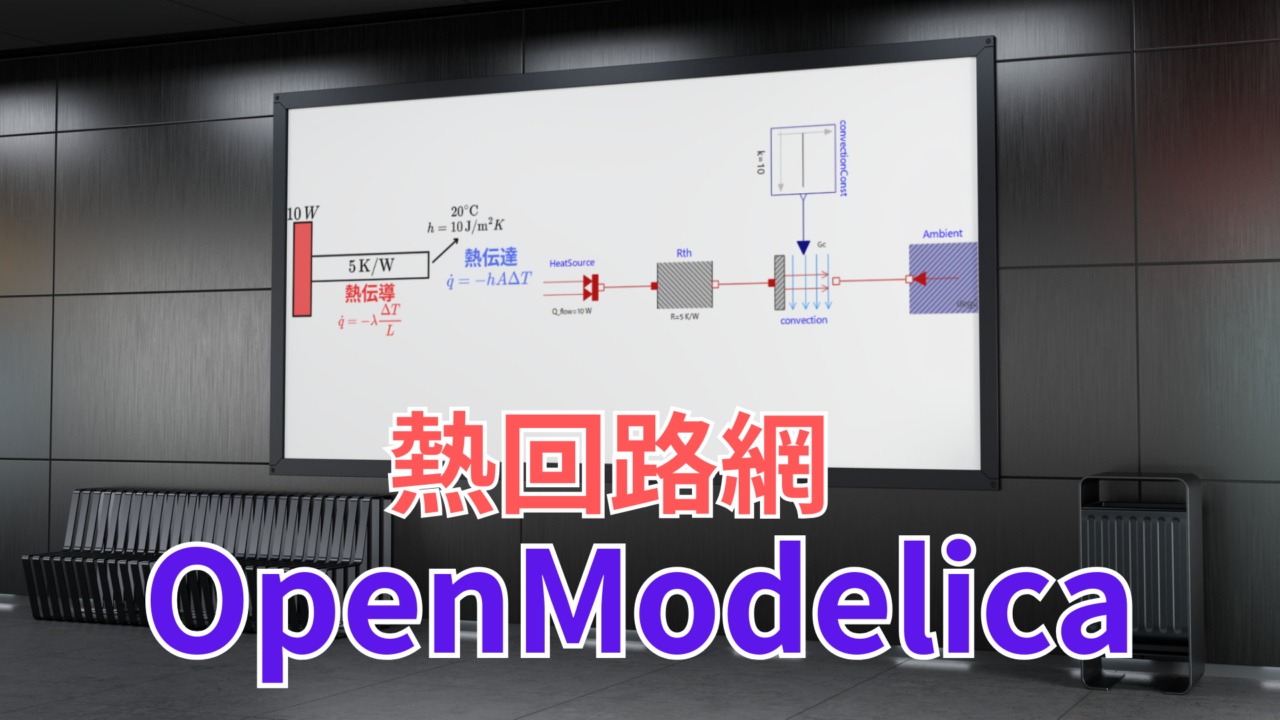
以下のような現象をOpenModelicaで再現します。

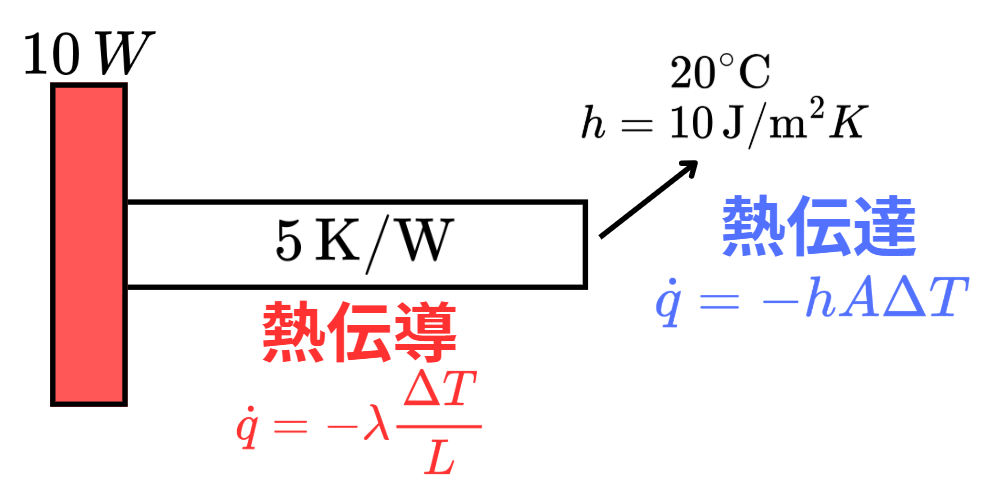
固体の左端を$10\text{W}$で温めている状態で、固体に接触しています。また、固体右端は空気と接しているため、熱伝達によって熱が奪われます。
固体には熱抵抗$R_{th}=5\text{K}/\text{W}$があるので、固体の左右で温度差が生じるというシンプルなモデルです。

こちらの現象を再現するには、以下の式を立てることになります。

熱伝導：$\dot{Q}=-\lambda A\frac{\Delta T}{L}$
熱伝達：$\dot{Q}=-hA\Delta T$

単位時間当たりの熱量$\dot{Q}$は固体を一定値で伝わるため、左から右へ$10\text{W}$で伝わっていくことになります。

熱流束：$\dot{q}=\frac{\dot{Q}}{A}$
断面積：$A$ ※今回は$A=1\,\text{m}^2$
熱伝導率：$\lambda$
長さ：$L$

熱伝導と熱伝達の理解はこちらの記事をご参考ください。

熱伝導

固体は温度が高い場合に振動エネルギーが大きくなり、隣の原子と相互作用しながら高温から低温側へ熱を伝播します。
これが熱伝導です。

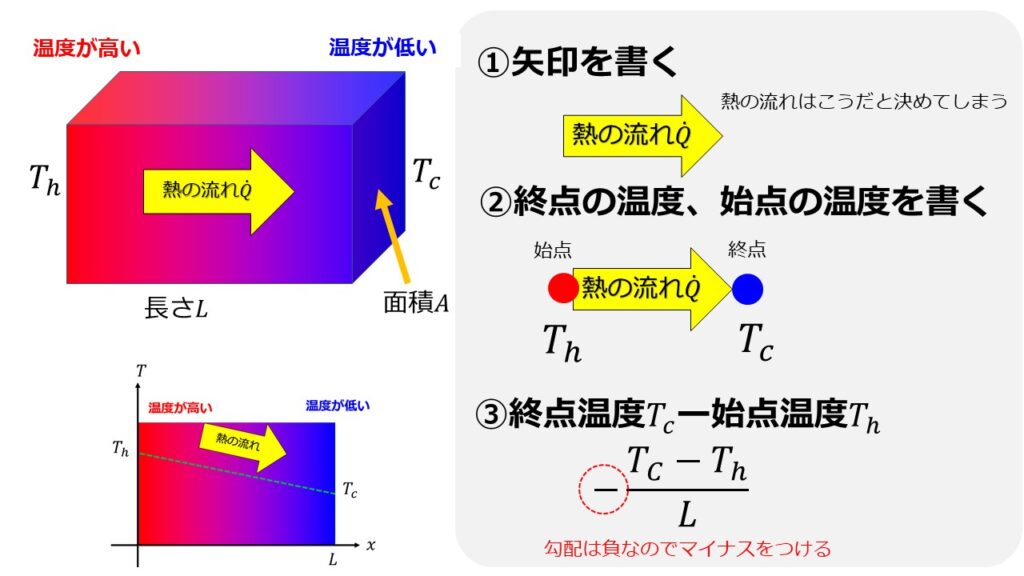
フーリエの法則により$\dot{Q}=-\lambda A\frac{\Delta T}{L}$ですが、電気回路との類似を考えて熱抵抗という形にすることができます。

こちらは電気回路で考えると以下の式になります。

\begin{align*}
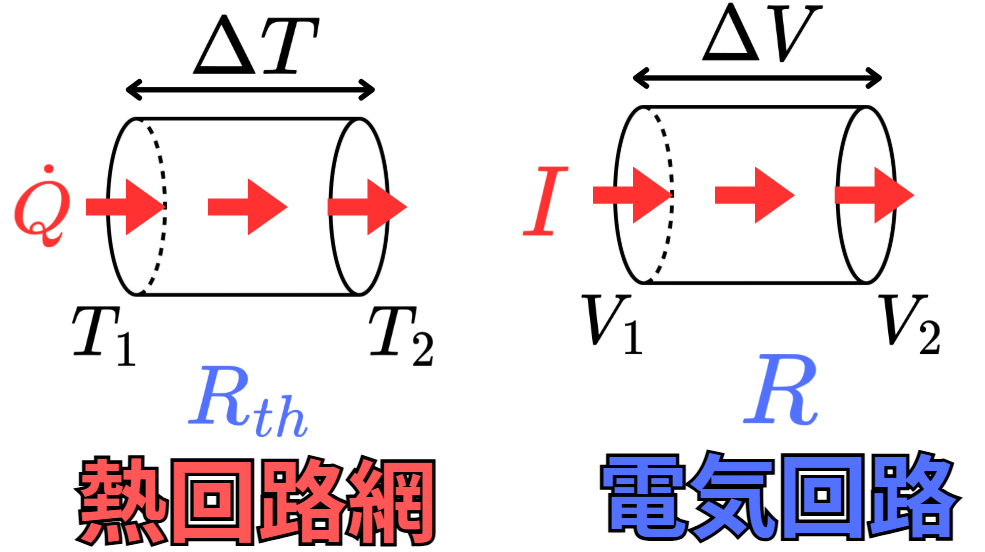
\Delta V=RI
\end{align*}

こちらはオームの法則ですね。
両端の電圧差$\Delta V$があれば、抵抗$R$に応じた電流$I$が発生するというモノです。

この類似から熱回路網に当てはめると$\dot{Q}=-\lambda A\frac{\Delta T}{L}$は以下の式とします。

\begin{align*}
\Delta T=R_{th}\dot{Q}
\end{align*}

$R_{th}=\frac{L}{\lambda A}$が熱抵抗になります。
※ただし、温度差による符号は省略しています。

OpenModelicaの熱抵抗のモデルもこの形をしています。

熱伝達

熱伝導と流体の流れである対流に基づいた熱移動が行われます。
これが対流熱伝達です。
※単に熱伝達という場合もあります。

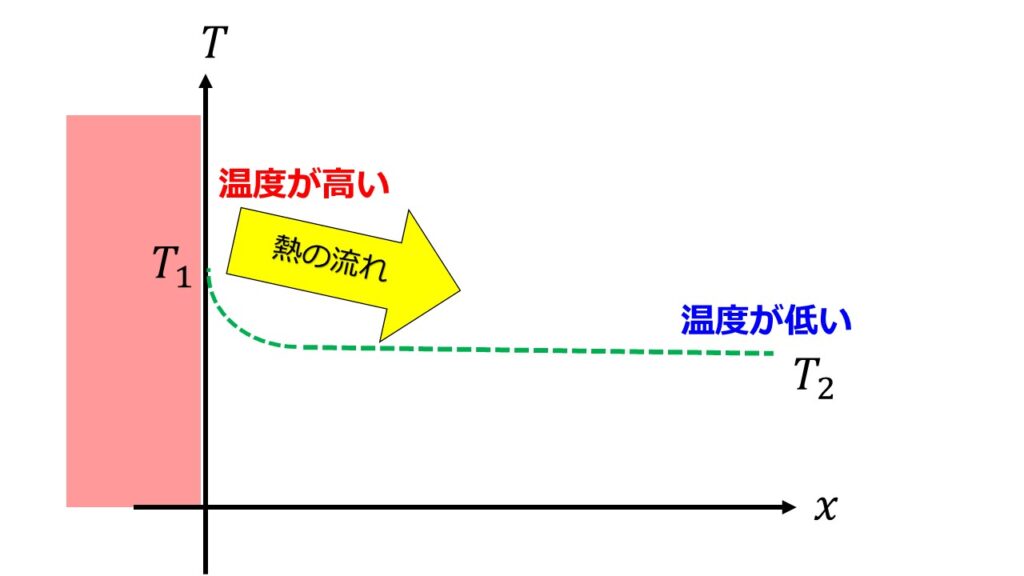
ニュートンの冷却法則により$\dot{Q}=-hA\Delta T$ですが、電気回路との類似を考えて熱抵抗という形にすることができます。

こちらは電気回路で考えると以下の式になります。

この類似から熱回路網に当てはめると$\dot{Q}=-hA\Delta T$は以下の式とします。

\begin{align*}
\Delta T=R_{conv}\dot{Q}
\end{align*}

$R_{cov}=\frac{1}{hA}$が熱抵抗になります。
※ただし、温度差による符号は省略しています。

OpenModelicaの熱伝達のモデルは上式ではなく、以下の式で定義されています。

\begin{align*}
\dot{Q} = G_{c}\Delta T
\end{align*}

※熱コンダクタンス：$G_{c}=hA$

モデル作成

モデル作成の雰囲気をわかってもらうために動画にしました。

解説はありませんが、雰囲気わかってもらえればOKです。

操作としては以下のようにアイコンをドラッグ＆ドロップとアイコン同士を接続していくだけでモデルが作成できます。

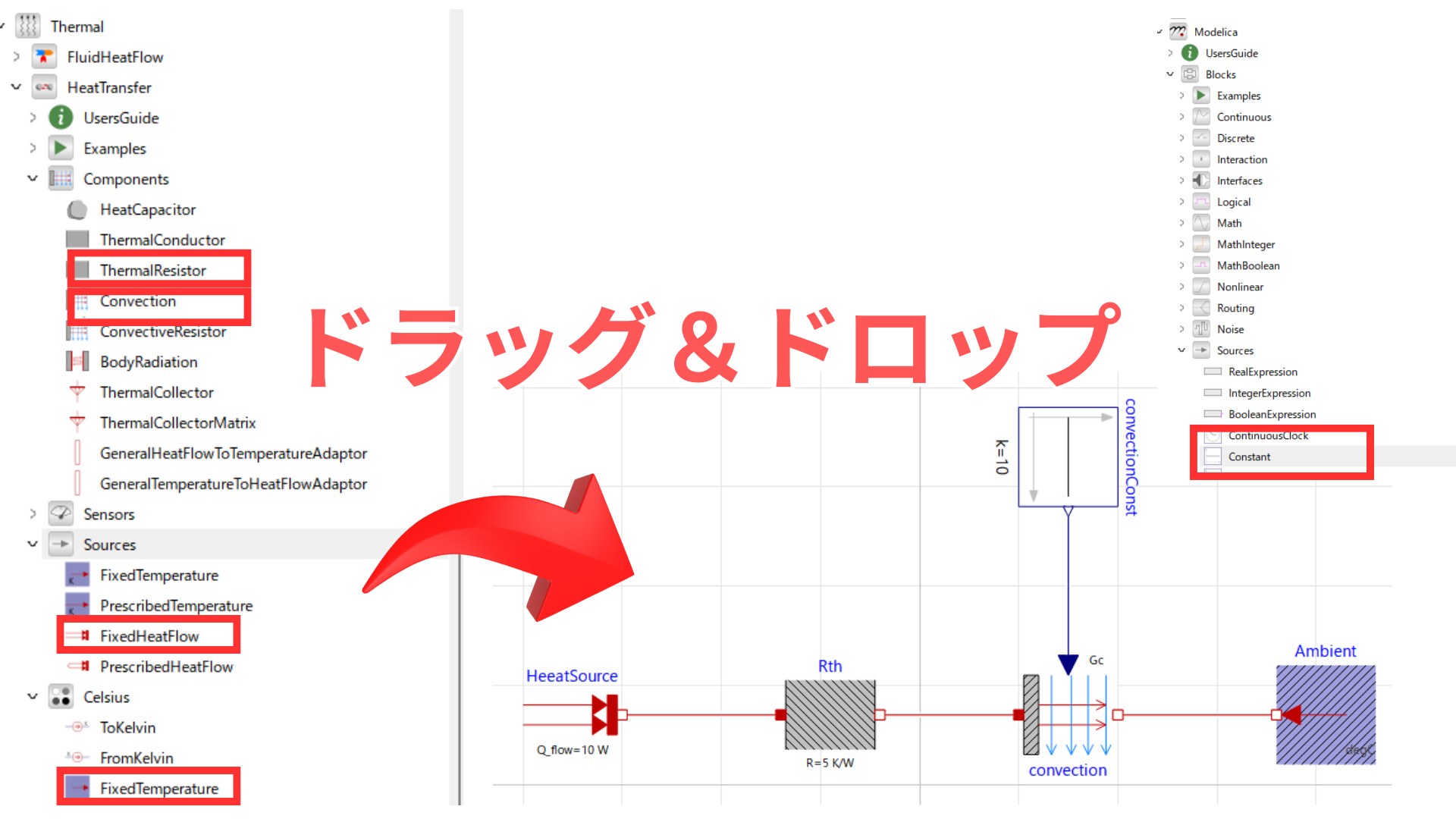
理論の解説

モデルを作成できたので理論の解説も行います。

今回作成したOpenModelicaのモデルは、以下のような構成になっています。

モデル名	パラメータ	支配方程式
熱伝導：ThermalResistor	R（熱抵抗）	dT = R × Q
熱伝達：ThermalConductor	G（熱コンダクタンス）	Q = G × dT

プログラムの中を確認して何をやっている見ておくことで理解が深まりますし、計算がうまくいっているのかを確認することができます。

各アイコン上で右クリックし、「クラスを開く」をクリックすると、部品ごとの情報を調べることができます。
プログラムを以下の手順で調べてみましょう。

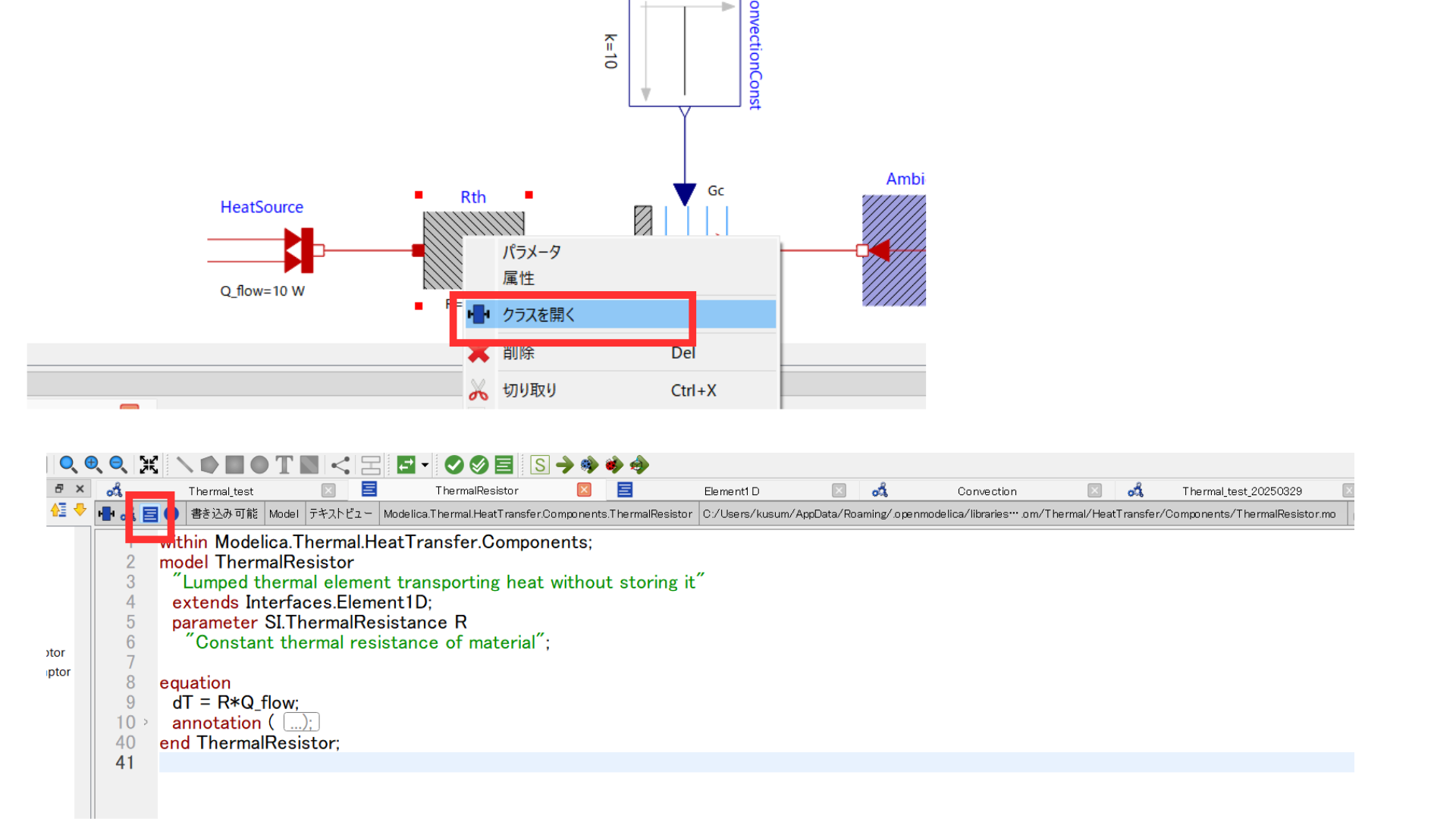
熱抵抗のモデル

model ThermalResistor

1	model ThermalResistor

このモデルは「熱を蓄積しないが、輸送はする部品（熱抵抗体）」を表します。名前の通り 熱抵抗（Thermal Resistance） を使って、2点間の温度差と熱流（heat flow）との関係をモデル化します。

extends Interfaces.Element1D;

1	extends Interfaces.Element1D;

このモデルは Interfaces.Element1D を継承しています。これは熱流（Q_flow）と温度差（dT）を扱う1次元の熱要素としての基本的な入出力インタフェースを示しています。

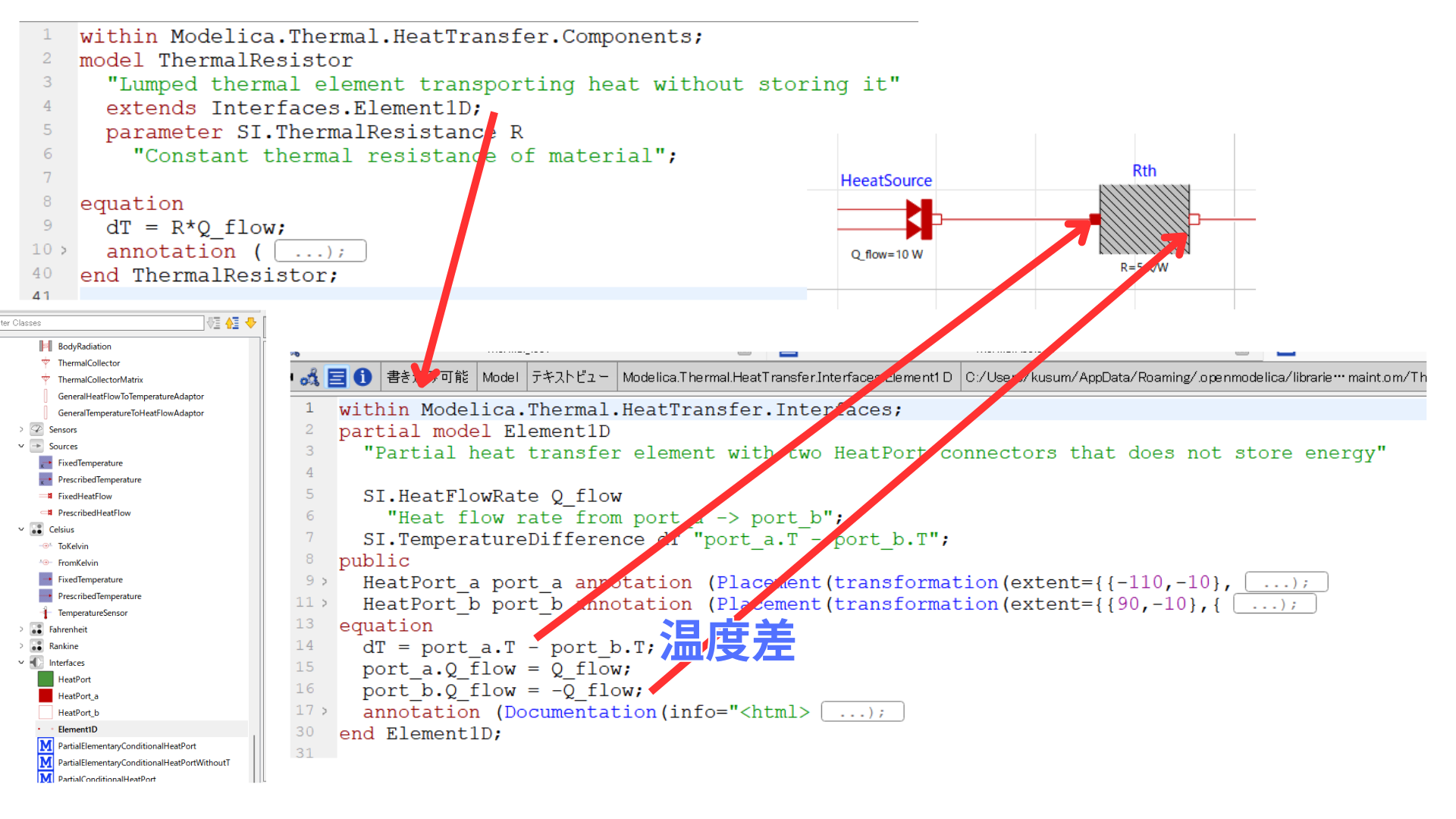
左側ポートでの温度と右側ポートでの温度差をdTとして定義しています。

equation
  dT = R * Q_flow;

1 2	equation dT = R * Q_flow;

この式は オームの法則の熱版を表しています：

ΔT = R × Q

1	ΔT = R × Q

電気で言えば、V = R × I と同じ考え方です。

つまり、左側のポートでのQ_flowは$10\text{W}$、熱抵抗が$5.0\text{k}\/text{W}$なので、熱抵抗部分の温度差dTは$50^\circ\mathrm{C}$となります。

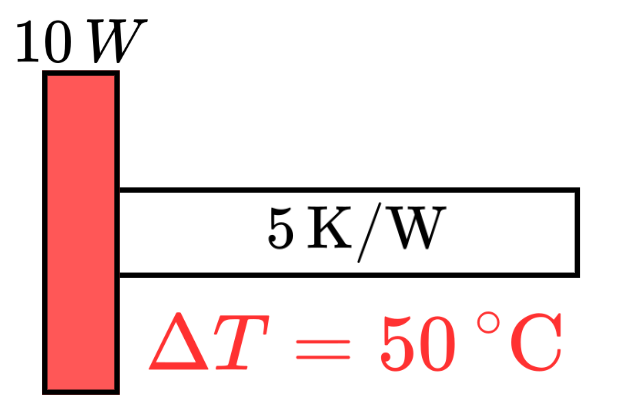
両端の温度がわかったわけではなく、計算式から温度差$\Delta T$がわかったということです。
両端の温度はのちほどわかります。

熱伝達のモデル

model Convection
  "Lumped thermal element for heat convection (Q_flow = Gc*dT)"

model Convection

"Lumped thermal element for heat convection (Q_flow = Gc*dT)"

このモデルは、熱対流（convection） を表す部品です。温度差によって熱が移動する現象をシンプルにモデル化しており、基本式は以下の通りです。

Q_flow = Gc * ΔT

1	Q_flow = Gc * ΔT

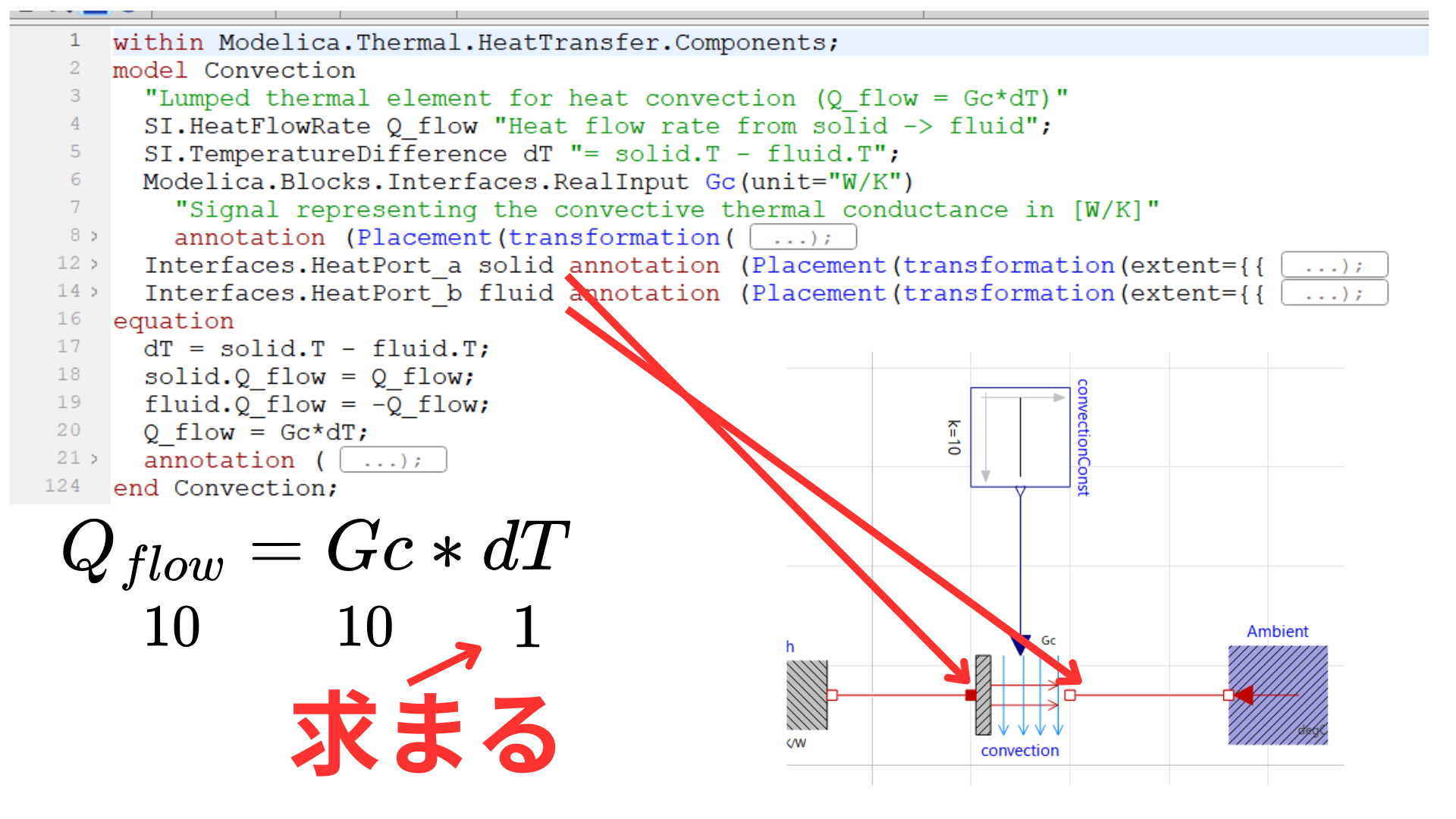
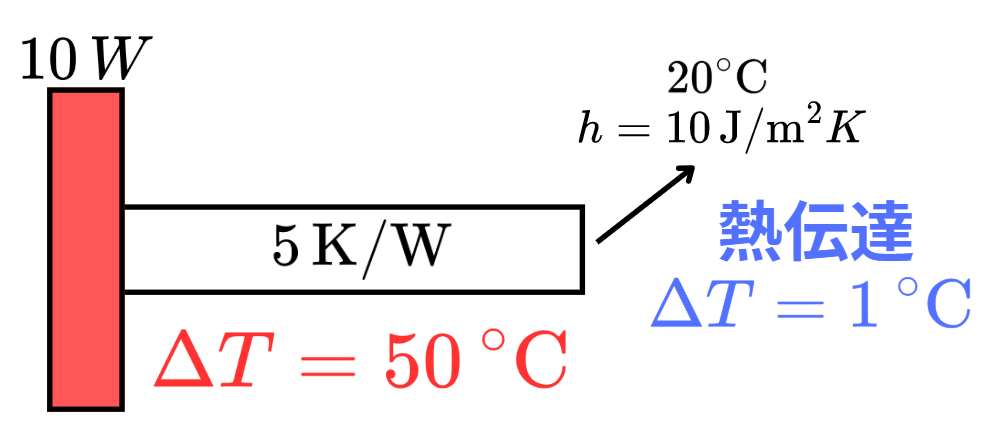
つまり、左側のポートでのQ_flowは$10\text{W}$、熱コンダクタンス$G_c = 5.0\text{W}\/text{K}$なので、熱伝達での温度差dTは$1^\circ\mathrm{C}$となります。

このような形で温度差だけが計算されたことになります。

SI.TemperatureDifference dT "= solid.T - fluid.T";

1	SI.TemperatureDifference dT "= solid.T - fluid.T";

dT は、固体と流体間の 温度差 を表します。単位は ℃（摂氏） です。

温度差dT=1と決まっており、fluid.T=20（外気温度℃）なので、solid.T=1.0と決まります。

それぞれ固体の両端の温度差と熱伝達部分の外気との温度差がわかったので、あとは芋づる式で温度が計算できます。

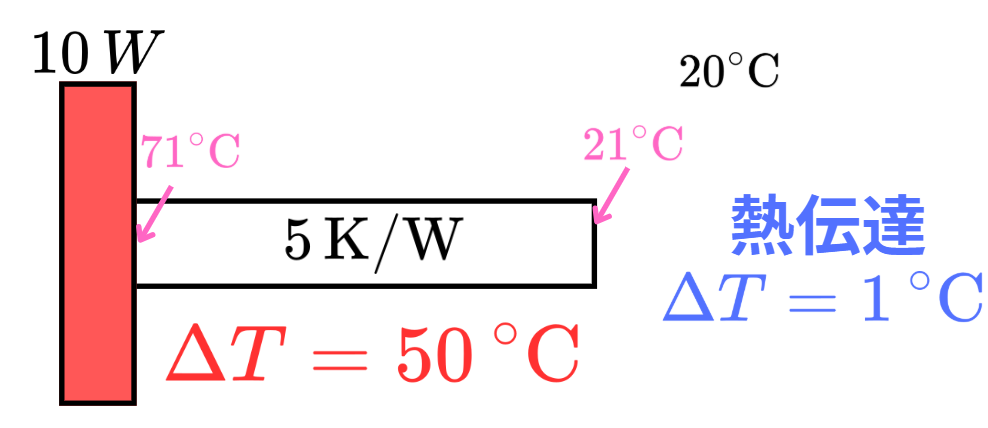
実際にOpenModelicaで確認してみましょう。

計算実行後に「プロット」タブに切り替わるので、数値を確認することができます。

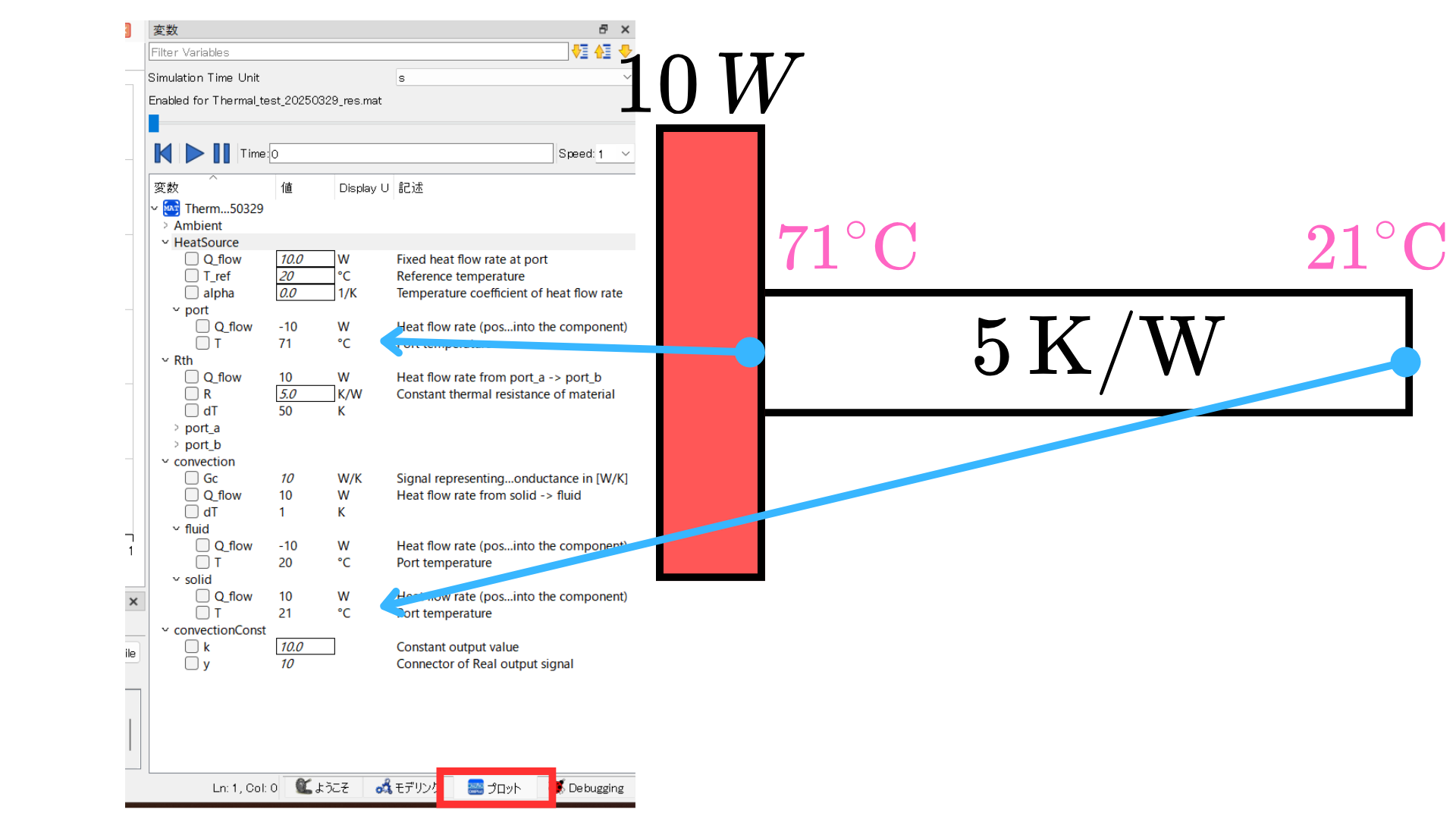
理論通りになっていますね！

まとめ

本記事で示したように、OpenModelicaを使えば、熱抵抗や熱伝達といった伝熱の基本モデルを直感的に組み立てられることを示しました。

すごく簡単に1Dモデルを作成できて簡単にシミュレーションまでできました。
本記事の内容のような簡単なモデルであれば、おそらくソフトを起動して1分も経たずに計算実行までできたのではないでしょうか。

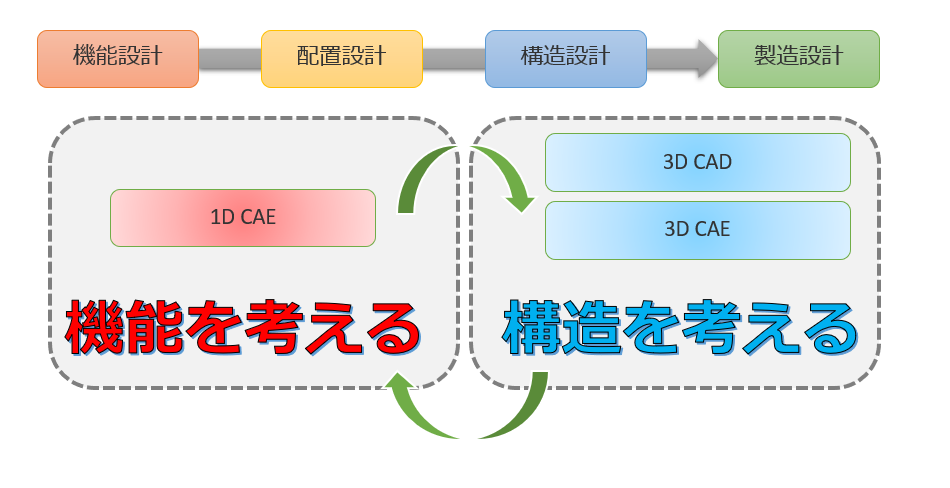
1DCAEの嬉しさは大きく分けて2つあると個人的に考えています。

1つ目が機能を考えるです。
製品を作る前の段階で部品同士を組み合わせたシステム全体として「何がしたいのか」「何ができるのか」を検討する上で、大きな力を発揮します。アイデア段階で性能や挙動を予測できるのは、設計の自由度や効率を大きく高めてくれるはずです。
1D CAEは実体のあるモノを直接扱うわけではないため、モデル作成には少し癖を感じるかもしれません。

2つ目がXにも投稿しましたが、分野をまたいだ考察をできるです。

1D CAEの再学習をしている。
1D CAEは「物理的考察がしやすい」「計算時間が速い」というメリットがよく言われるけど、個人的には分野をまたいでシステムとして計算できるというところが最大のメリットと思っている。
例えば、力学、流体、熱、電気これを3Dで連成させるのは厳しいが1D CAEなら容易。 pic.twitter.com/RMLcq7ewzY

— カマキリ🐲CAE頑張る (@t_kun_kamakiri) March 22, 2025