こんにちは(@t_kun_kamakiri)(‘◇’)ゞ
本記事では、伝熱工学の基本である以下の熱の伝わり方について解説を行います。
当ブログでは以下のような構成で記事を書いていきます。
- 【伝熱工学の基礎】熱伝導、熱伝達、熱放射をわかりやすく解説
- 【熱伝導とは?】熱の伝わり方の仕組みとフーリエの法則を図で解説
- 【対流熱伝達とは?】熱の伝わり方の仕組みとニュートンの冷却法則を図で解説
- 【ふく射熱とは?】熱の伝わり方の仕組みとステファン・ボルツマンの法則を図で解説
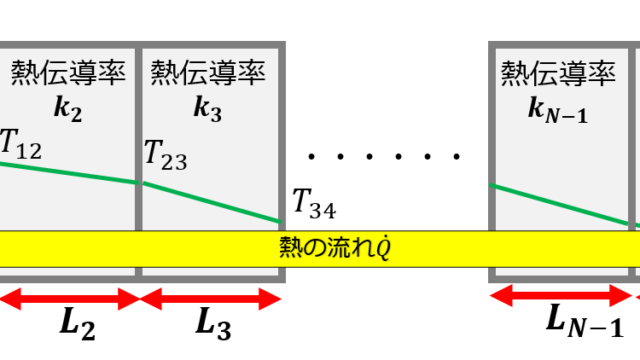
- 多層平板における合成の熱伝達率の導出
伝熱工学の基礎的な内容を網羅できるようにわかりやすく解説をしていきます。
- 工学系の学生
- 製造業に勤める技術者
- 技術士を目指している技術者
本記事は、伝熱工学の学ぶにあたって熱の伝わり方の3つの種類について解説を思います。
まずは基本的なことを頭に入れて全体像をつかみましょう。
熱の伝わり方の基本
まずはじめに熱の伝わり方の基本を押さえましょう。
これは熱力学第二法則と呼ばれる法則に関係しています。
固体・液体・気体の物質において、人が手を加えなければ自然に起こりうるのは「温度の高い方から低い方へ熱が流れる」というものです。
これをイメージで分かるように書くと以下のようになります。
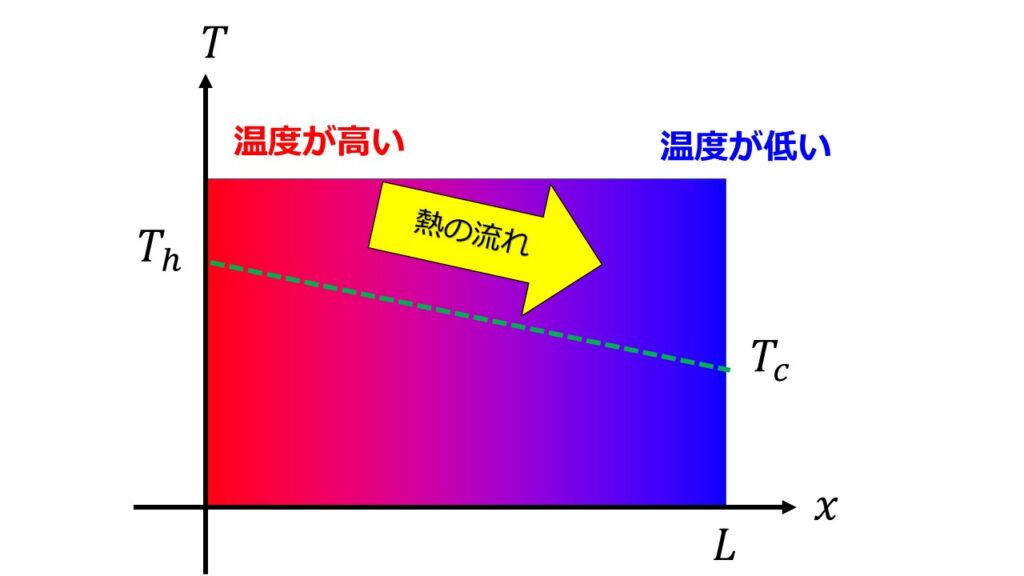
まるで坂道を転がるように熱移動が行われます。
この、高温から低温に坂道を転がるように熱移動が行われるのを数式表すと、
-\frac{T_{c}-T_{h}}{L}\tag{1}
\end{align*}
となります。
マイナスは傾き(勾配)が負になっているのことからきています。
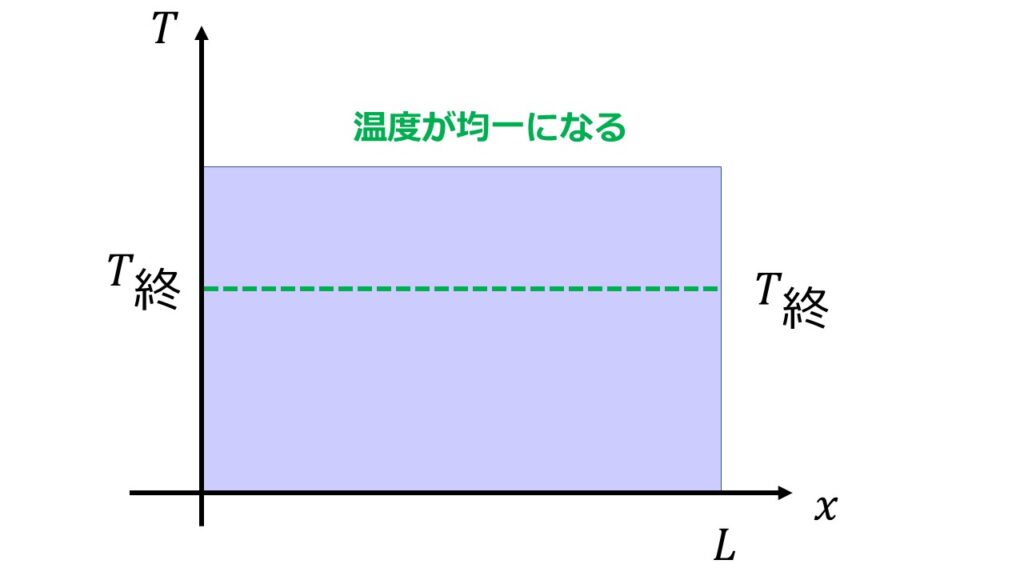
温度差があることで熱移動が起こり最終的には温度が均一になって熱移動が行われなくなります。
※厳密には熱移動がおこなわれなくなるというのは語弊がありますが、ミクロな視点で見ると原子間の熱移動は行われていますが、伝熱工学や熱力学ではマクロな視点で熱移動が行われたかどうかを見ています。
温度差が熱移動が起こる
温度差によって熱移動が生じることがわかったところで、式を書く際にこんなことを思うときがあります。
このような疑問に答えるためには自分の中のルールを決めておく必要があります。
あくまで参考ですが、僕は以下のようにルールを作って式を立てています。
※熱伝導の式を例にしています。
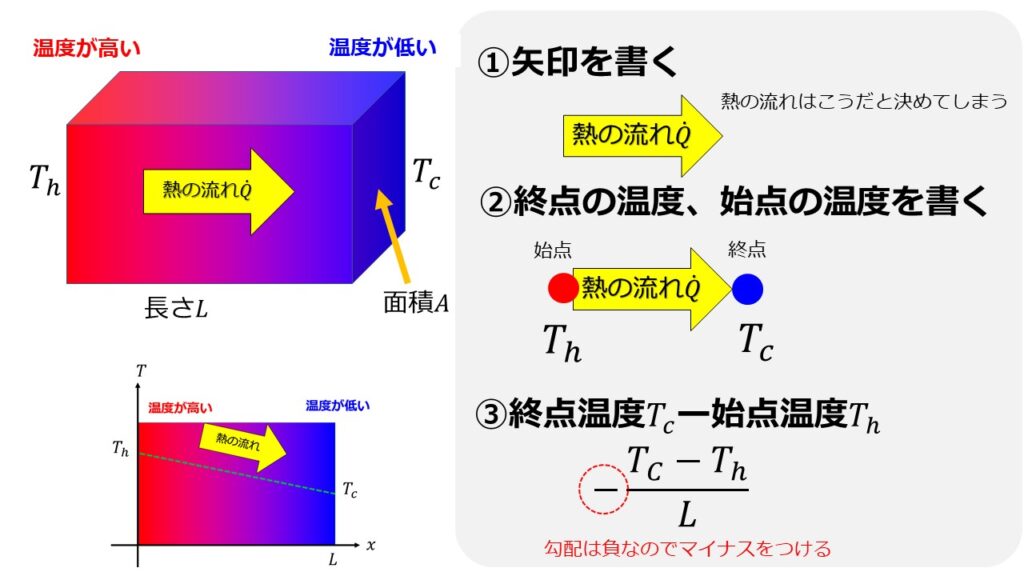

最終的に熱量は$-\frac{T_{c}-T_{h}}{L}$で伝わることになります。
このとき、分子の符号によって矢印の向きが変わります。
- $T_{c}<T_{h}$であれば$-\frac{T_{c}-T_{h}}{L}>0$なので矢印の向きは図の通りになる。
- $T_{c}>T_{h}$であれば$-\frac{T_{c}-T_{h}}{L}<0$なので矢印の向きは図の向きと反対になる。
矢印の向きは熱の移動の方向を示すものなので、矢印の向きが反対であるということは熱移動の方向が図とは逆だったということになります。
このように決めたルールに従って立式して、$-\frac{T_{c}-T_{h}}{L}$の符号で矢印の向き(熱量の向き)が決まるということです。
熱移動には3つの種類がある
熱移動は温度差があることで生じるということを上で述べました。
この基本的なことを押さえておきつつ、その熱移動の種類には以下の3つに分けられることを覚えておきましょう。
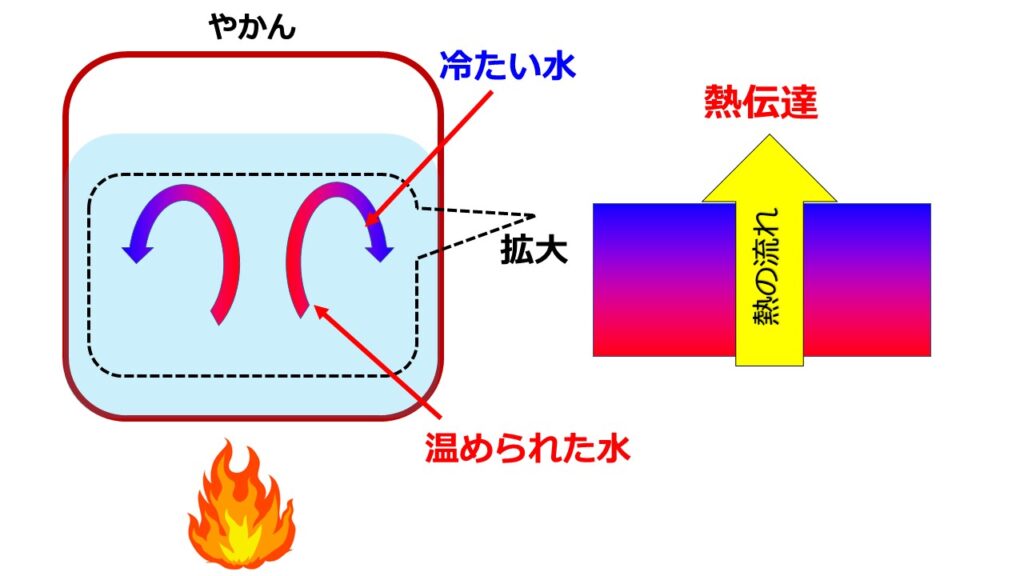
これらをわかりやすく「水を入れたやかんを温めた場合」で解説を行います。


熱伝導
熱伝導の仕組み
熱伝導の仕組みを絵を用いて解説します。
固体は温度が高い場合に振動エネルギーが大きくなり、隣の原子と相互作用しながら高温から低温側へ熱を伝播します。
これが熱伝導です。
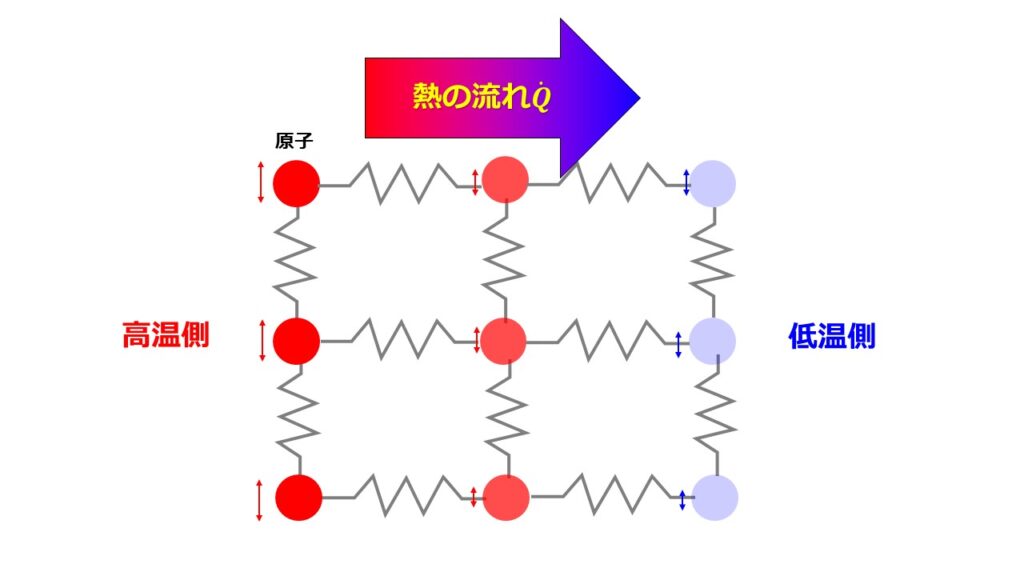

金属の場合は自由電子が存在し、自由電子の運動エネルギーを低温側へ伝えることができるため金属の場合の熱伝導率は大きくなります。
水の入ったやかんの例では、やかんの鉄の部分の熱移動が熱伝導になります。
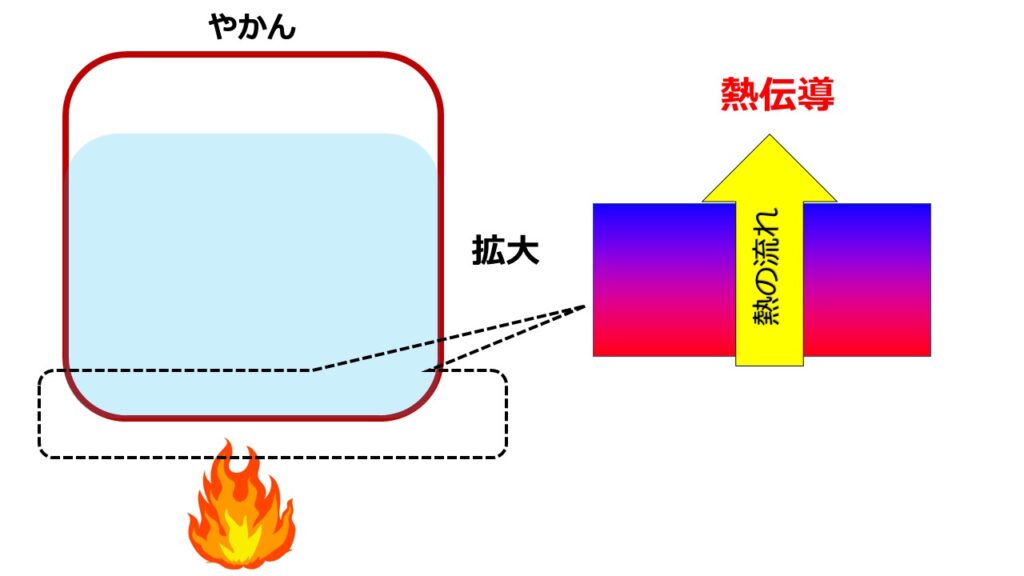

フーリエの法則
熱伝導に関係する式には、単位面積・単位時間当たりの熱移動と単位長さあたりの温度差を熱伝導率という比例係数で結んだフーリエの法則があります。
\dot{q}=-k\frac{dT}{dx}\tag{2}
\end{align*}
熱伝導率:$k[W/m K]$
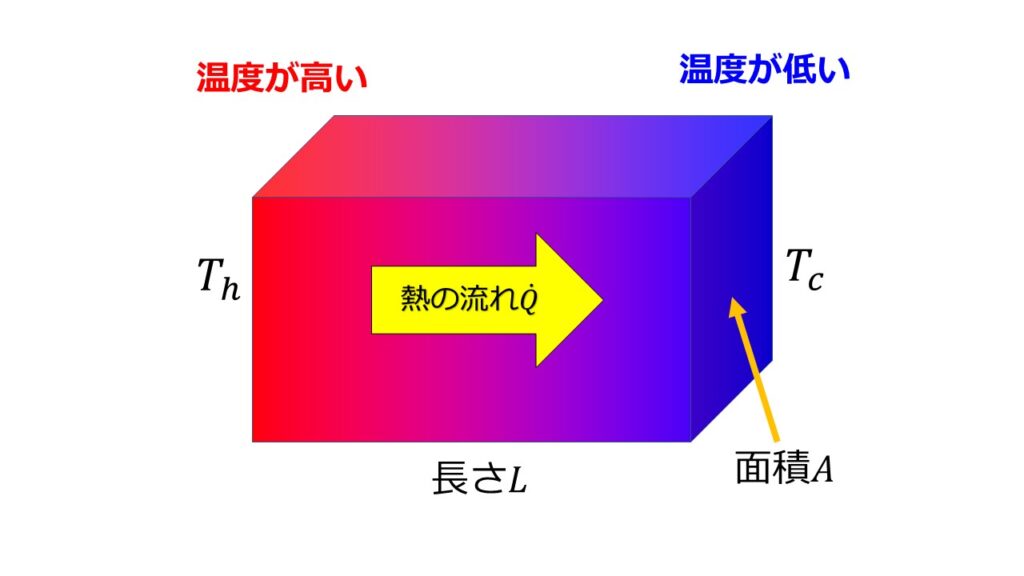
フーリエの法則は単位時間当たりの熱量$\dot{Q}$は、単位長さ当たりの温度差$\frac{T_{c}-T_{h}}{L}$と面積$A$に比例するとして、$\dot{Q}=-kA\frac{T_{c}-T_{h}}{L}$より、
- 左辺:単位面積・単位時間あたりの熱量:$\frac{\dot{Q}}{A}=\dot{q}$
- 右辺:単位長さあたりの温度差:$-\frac{T{c}-T_{h}}{L}=-\frac{dT}{dx}$
が比例するという考えのもと導かれています。
※ただし、熱伝導率は温度依存性があります。
これは熱量を温度差とを無理やり結びつけたことによる理論的な不足分が表れている結果です。より詳しい理解のためには量子力学や統計力学を駆使することになり、ここでは割愛します_(._.)_
対流熱伝達
対流熱伝達の仕組み
対流熱伝達の仕組みを絵を用いて解説します。
熱伝導と流体の流れである対流に基づいた熱移動が行われます。
これが対流熱伝達です。
※単に熱伝達という場合もあります。
- 自然対流
温度差(高温だと密度が小さい)で発生する浮力による対流 - 強制対流
機械的な手段で強制的に作られた対流 - 沸騰
液体が気体になるときの蒸発潜熱による熱移動 - 凝縮
気体が液体になるときの熱移動
どのような流れかによって熱の輸送度合いが変わります。
後ほど説明する熱伝達率の値の大きさに関わります。
ニュートンの冷却法則
熱伝達に関係する式には、単位面積・単位時間当たりの熱移動と温度差を熱伝導率という比例係数で結んだニュートンの冷却法則があります。
フーリエの法則とよく似た形をしています。
\dot{q}=-h\big(T_{2}-T_{1}\big)\tag{3}
\end{align*}
熱伝達率:$h[W/m^2 K]$
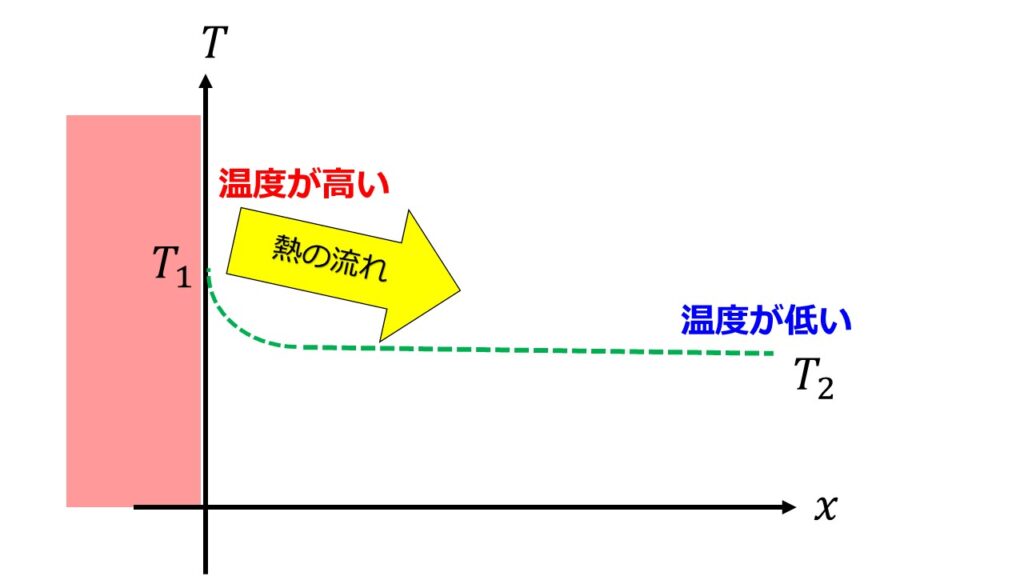
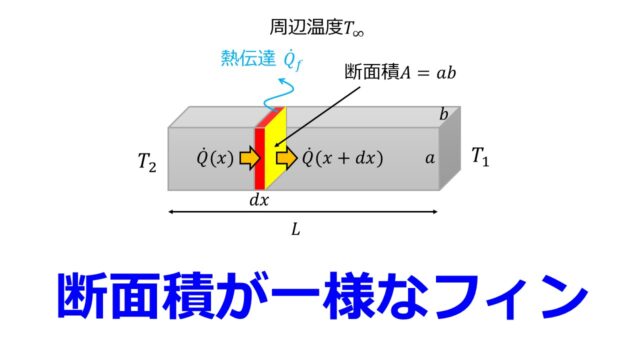
ニュートンの法則である単位時間当たりの熱量$\dot{Q}$は、物体表面の温度と流体の温度との温度差$T_{2}-T_{1}$と面積$A$に比例するとして、$\dot{Q}=-hA(T_{2}-T_{1})$より、
- 左辺:単位面積・単位時間あたりの熱量:$\frac{\dot{Q}}{A}=\dot{q}$
- 右辺:単位長さあたりの温度差:$-(T_{2}-T_{1})$
が比例するという考えのもと導かれています。

対流熱伝達の難しいところは、流れによって熱伝達率が決定されるため物性値を持たないということです。
なので、自然対流なのか強制対流なのかで熱伝達率が変わるため、どういった流れなのかを知ることは重要です。
ふく射熱
ふく射熱の仕組み
物体表面から可視光や熱外線などの電磁波に変換されて放射される際の熱移動をふく射熱といいます。
やかんを温めるときの火からやかんに伝わる熱移動がそれに相当します。
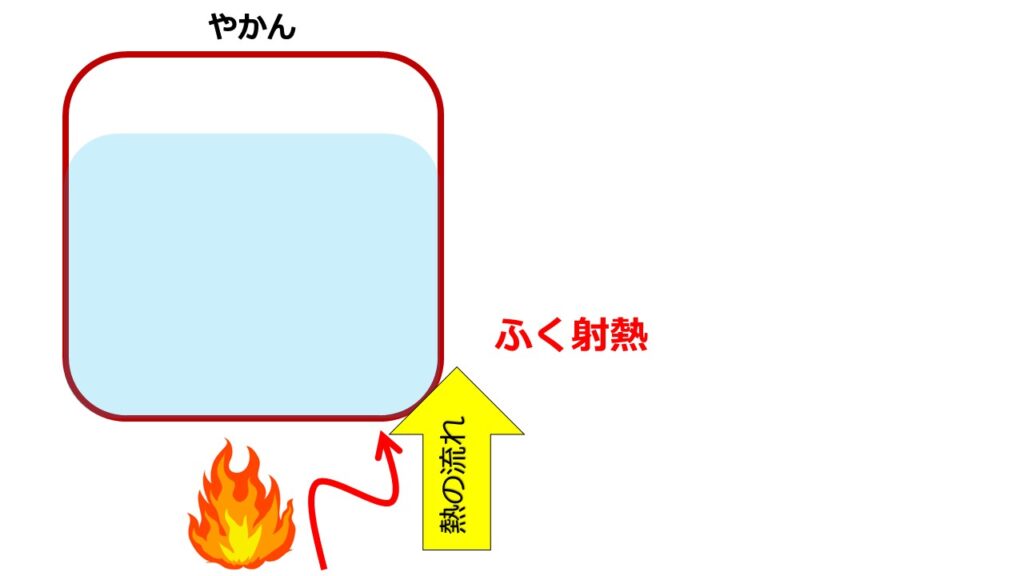

ふく射熱は原子や分子の振動による電磁波なので、熱伝導や熱伝達のような熱をつたえる媒体がなくても熱を伝えることができるのが特徴です。つまり、ふく射熱は真空状態でも伝わる熱輸送です。
他の例では太陽の熱が地球に伝わる熱もふく射熱ですね。
電磁波自体は熱ではありませんが、電磁波が真空中を伝わってきて物体に当たるとそのエネルギーをもらって原子や分子が激しく振動することにより温まります。
これがふく射熱によって物体が温まる原理です。
この仕組を利用した身近なものが電子レンジですね。
ステファン・ボルツマンの法則
ふく射熱にも熱伝導や熱伝達同様に温度差による単位面積あたり、単位時間当たりの熱量の式があります。
\dot{q}=-\varepsilon\sigma\big(T_{2}^{4}-T_{1}^{4}\big)\tag{4}
\end{align*}
- 放射率:$\varepsilon$
- ステファン・ボルツマン定数:$\sigma=5.67\times 10^{-8}[W/m^2\cdot K^4]$
熱力学と伝熱工学の違い
熱を扱う分野には熱力学や熱工学というものがあります。
今回紹介した伝熱工学との違いは何でしょうか?
つまり、熱力学は時間的変化や空間的変化も基本的には考慮していないということです。
丸っと温度$T$などとマクロな視点で状態を定義しています。
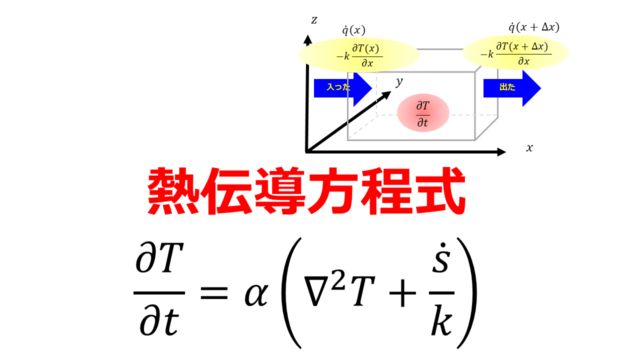
つまり、伝熱工学は時間的変化や空間的変化も考慮しているということです。
まとめ
熱移動には3種類あります。
おすすめ参考書
伝熱工学の基礎勉強のための参考書と演習問題を紹介します。











ステファンボルツマンのやつですが、T^4ではないですか?
ご指摘ありがとうございます。
フーリエの冷却法則じゃなくてニュートンの冷却法則ではないですか?
あとステファン・ボルツマン定数の10のべき乗部分は10^-8ではないですか?
ご指摘ありがとうございます。
修正しました。