解析力学

ポアッソン括弧を用いた関係式

 

『計算過程はどうでも良い。

結果だけ知ってさえいれば十分である。

しかし、計算過程を手を動かして進めることで、「何が出発点」で「何の結果」を得たのか・・・・

そしてその結果のための「条件は何か」を深く知ることになるでしょう。』

by　宇宙に入ったカマキリ

 

というわけで、結果だけ覚えておけば問題ないのですよ、このポアッソン括弧というものは(笑)

ポアッソン括弧の表式を学んだところで、それを用いて導かれる関係式を丸暗記して覚えておくと良いでしょう(^^)/

 

前回の記事です。
ポアッソン括弧の定義式を書きました。

 

ポアッソン括弧式というのは、

\(\{q_{i}\},\{p_{i}\}\)を変数とする、関数\(f(\{q_{i}\},\{p_{i}\})\)と\(g(\{q_{i}\},\{p_{i}\})\)に対して、

\begin{align*}\{f,g\}_{q,p}=\sum_{i}\big( \frac{\partial f}{\partial q_{i}}\frac{\partial g}{\partial p_{i}}-\frac{\partial f}{\partial p_{i}}\frac{\partial g}{\partial q_{i}}\big)\cdot\cdot\cdot (1)\end{align*}

です。

 

なーんにも特別なことはないです(笑)
この謎の偏微分の複雑な形を、上記のように”括弧”と表記して簡単な表式に書き直しただけです。
これを「ポアッソン括弧式」と言う・・・・ただそれだけです。

 

そして、これらの表式はよく計算途中で登場するので、「括弧を使って表式をまとめてやる」って感じで覚えておくと良いでしょう。

このありがたさがわかるのは、

変数\(\{q_{i}\},\{p_{i}\}\)から、それらを変数とした別の変数\(\{Q_{i}\},\{P_{i}\}\)（正確には\(\{Q_{i}(\{q_{i}\},\{p_{i}\})\},\{P_{i}\}(\{q_{i}\},\{p_{i}\})\)）のように正準変換した際に気付くことになります。

 

では本日の内容です。

ポアッソン括弧を使って下記の関係式を証明します。

\begin{align*}\{q_{i},q_{j}\}_{q,p}=0\end{align*}

\begin{align*}\{p_{i},p_{j}\}_{q,p}=0\end{align*}

\begin{align*}\{q_{i},p_{j}\}_{q,p}=\delta {ij}\end{align*}

\(\delta _{ij}\)はクロネッカーデルタと呼ばれます。

いきなりだと慣れない人がいるかもしれませんが、クロネッカーデルタ\(\delta _{ij}\)は、

\(i=j\)ならば、
\(\delta {ij}=1\)

\(i\neq j\)ならば、
\(\delta {ij}=0\)

となる場合分けの記号です。

 

ではさっそくやっていきましょう(^^)/

スポンサーリンク

目次
  1. \(\{q_{i},q_{j}\}_{q,p}=0\)の証明
  2. \(\{p_{i},p_{j}\}_{q,p}=0\)の証明
  3. \(\{p_{i},q_{j}\}_{q,p}=\delta_{ij}\)の証明
  4. まとめ
  5. 正準変換の概要

\(\{q_{i},q_{j}\}_{q,p}=0\)の証明

 

 

証明も何もないのですが、ただポアッソン括弧を使って素直に式変形するだけです。

ポアッソン括弧、

\begin{align*}\{f,g\}_{q,p}=\sum_{k}\big( \frac{\partial f}{\partial q_{k}}\frac{\partial g}{\partial p_{k}}-\frac{\partial f}{\partial p_{k}}\frac{\partial g}{\partial q_{k}}\big)\cdot\cdot\cdot (1)\end{align*}


※変数\(q_{i}\)などの\(i\)と文字がかぶっているので、ポアッソン括弧の右辺の和の\(i\)を\(k\)に書き直しておきます。

 

\(f\)→\(q_{i}\)
\(g\)→\(q_{j}\)
と書き直すだけです。

\begin{align*}\{q_{i},q_{j}\}_{q,p}=\sum_{k}\big( \frac{\partial q_{i}}{\partial q_{k}}\frac{\partial q_{j}}{\partial p_{k}}-\frac{\partial q_{i}}{\partial p_{k}}\frac{\partial q_{j}}{\partial q_{k}}\big)\cdot\cdot\cdot (2)\end{align*}

ここで、変数\(\{q_{i}\},\{p_{i}\}\)は互いに独立であるので、

第一項：\(\frac{\partial q_{j}}{\partial p_{k}}=0\)
第二項：\(\frac{\partial q_{i}}{\partial p_{k}}=0\)

↑こんな感じで0になりますね。

なので、(1)は、

\begin{align*}\{q_{i},q_{j}\}_{q,p}=0\cdot\cdot\cdot (3)\end{align*}

 

 

 

\(\{p_{i},p_{j}\}_{q,p}=0\)の証明

 

 

これは、(3)を導出したときと全く同じようにします。
ポアッソン括弧、

\begin{align*}\{f,g\}_{q,p}=\sum_{k}\big( \frac{\partial f}{\partial q_{k}}\frac{\partial g}{\partial p_{k}}-\frac{\partial f}{\partial p_{k}}\frac{\partial g}{\partial q_{k}}\big)\cdot\cdot\cdot (1)\end{align*}

\(f\)→\(p_{i}\)
\(g\)→\(p_{j}\)
と書き直すだけです。

\begin{align*}\{p_{i},p_{j}\}_{q,p}=\sum_{k}\big( \frac{\partial p_{i}}{\partial q_{k}}\frac{\partial p_{j}}{\partial p_{k}}-\frac{\partial p_{i}}{\partial p_{k}}\frac{\partial p_{j}}{\partial q_{k}}\big)\cdot\cdot\cdot (4)\end{align*}

ここで、変数\(\{q_{i}\},\{p_{i}\}\)は互いに独立であるので、

第一項：\(\frac{\partial p_{j}}{\partial q_{i}}=0\)
第二項：\(\frac{\partial p_{i}}{\partial q_{i}}=0\)

↑こんな感じで0になりますね。

 

なので、(4)は、

\begin{align*}\{p_{i},p_{j}\}_{q,p}=0\cdot\cdot\cdot (5)\end{align*}

となります。

 

\(\{p_{i},q_{j}\}_{q,p}=\delta_{ij}\)の証明

 

これは、(3)(5)と少しだけ感じが違いますが難しくはないでしょう(^^)/

ポアッソン括弧、

\begin{align*}\{f,g\}_{q,p}=\sum_{k}\big( \frac{\partial f}{\partial q_{k}}\frac{\partial g}{\partial p_{k}}-\frac{\partial f}{\partial p_{k}}\frac{\partial g}{\partial q_{k}}\big)\cdot\cdot\cdot (1)\end{align*}

\(f\)→\(q_{i}\)
\(g\)→\(p_{j}\)
と書き直すだけです。

\begin{align*}\{q_{i},p_{j}\}_{q,p}=\sum_{k}\big( \frac{\partial q_{i}}{\partial q_{k}}\frac{\partial ,p_{j}}{\partial p_{k}}-\frac{\partial q_{i}}{\partial p_{k}}\frac{\partial p_{j}}{\partial q_{k}}\big)\cdot\cdot\cdot (6)\end{align*}

ここで、変数\(\{q_{i}\},\{p_{i}\}\)は互いに独立であるので第二項は0ですね。

そうすると、⑥式は少し見やすくなりまして、

\begin{align*}\{q_{i},p_{j}\}_{q,p}=\sum_{k}\big( \frac{\partial q_{i}}{\partial q_{k}}\frac{\partial p_{j}}{\partial p_{k}}\big)\cdot\cdot\cdot (7)\end{align*}

そこで、(6)式は\(i\)についての和をとっていますが、

変数\(\{q_{i}\},\{p_{i}\}\)は互いに独立であるという意味は、
変数\(q_{1},q_{2},q_{3},・・・,p_{1},p_{2},p_{3},・・・\)が互いに独立という意味です。

 

ですので、(7)式は\(k\)について和を取るのですが、\(k=i\)かつ\(k=j\)なら1ですが、それ以外は全部0になってしまいます。

ゆえに、(4)は、

\begin{align*}\{p_{i},p_{j}\}_{q,p}=\delta_{ij}\cdot\cdot\cdot (8)\end{align*}

 

 

まとめ

 

以上のようにして、

\begin{align*}[\{q_{i},q_{j}\}_{q,p}=0\cdot\cdot\cdot (3)\end{align*}


\begin{align*}\{p_{i},p_{j}\}_{q,p}=0\cdot\cdot\cdot (5)\end{align*}


\begin{align*}\{q_{i},p_{j}\}_{q,p}=\delta {ij}\cdot\cdot\cdot (8)\end{align*}

と、このようにポアッソン括弧式を使った関係式を導けました。

 

簡単でしたかね(^^)

このポアッソン括弧式のすごいところは、
変数\(\{q_{i}\},\{p_{i}\}\)から、それらを変数とした別の変数\(\{Q_{i}\},\{P_{i}\}\)（正確には\(\{Q_{i}(\{q_{i}\},\{p_{i}\})\},\{P_{i}\}(\{q_{i}\},\{p_{i}\})\)）のように正準変換した際も、

\begin{align*}\{Q_{i},Q_{j}\}_{q,p}=0\cdot\cdot\cdot (9)\end{align*}


\begin{align*}\{P_{i},P_{j}\}_{q,p}=0\cdot\cdot\cdot (10)\end{align*}


\begin{align*}\{Q_{i},P_{j}\}_{q,p}=\delta {ij}\cdot\cdot\cdot (11)\end{align*}

という関係は同じなのです。

(9)～(11)をポアッソン括弧式を使わずに書いたら、煩雑ですよ(笑)

そして、

(9)～(11)の関係式が成り立つことが、変数\(\{q_{i}\},\{p_{i}\}\)から別の変数\(\{Q_{i}\},\{P_{i}\}\)のような変換が正準変換であることの必要十分条件なのです。

↑とっても重要!(^^)!

正準変換って覚えていますか？

 

正準変換の概要

 

詳しくはこちらに書いております。

 

でも概要をもう一度書いておきます(^^)/

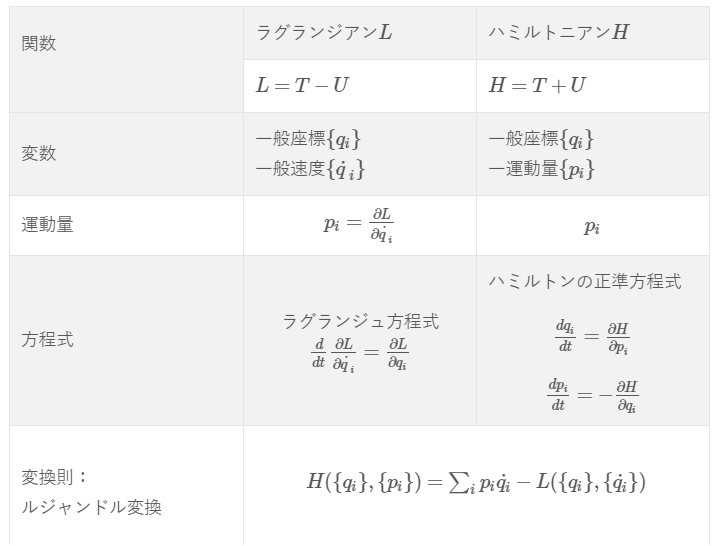
解析力学の枠組みでこのように座標の変換に対して基礎方程式（ラグランジュ方程式、ハミルトンの正準方程式）が変わらないとするだけでなくて、もっと一般的に運動量も含めて（すなわち、運動量も座標と同等の独立変数として扱う）、ハミルトンの正準方程式の形を不変に保つことができます。

式で書くと、

\begin{align*}Q_{i}=Q_{i}(\{q_{i}\},\{p_{i}\},t)\end{align*}

\begin{align*}P_{i}=P_{i}(\{q_{i}\},\{p_{i}\},t)\end{align*}

↑そういう変換ができるのです。

これを正準変換と言います。

ハミルトンの正準方程式の形を不変に保つようにするので、変換後も

ハミルトンの正準方程式

\begin{align*}\frac{dQ_{i}}{dt}=\frac{\partial {H}’}{\partial P_{i}}\end{align*}

\begin{align*}\frac{dP_{i}}{dt}=-\frac{\partial {H}’}{\partial Q_{i}}\end{align*}

が成り立ちます。

なので、変数\(\{q_{i}\},\{p_{i}\}\)から別の変数\(\{Q_{i}\},\{P_{i}\}\)のように、変換した後の変数\(\{Q_{i}\},\{P_{i}\}\)もハミルトンの正準方程式の形式を保っているような変換を正準変換と言います。

関連記事もどうぞ

COMMENT

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です