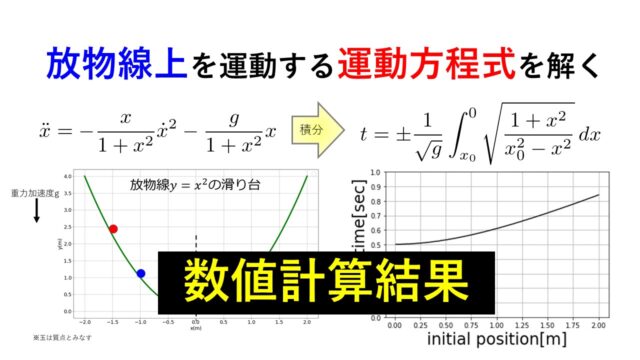
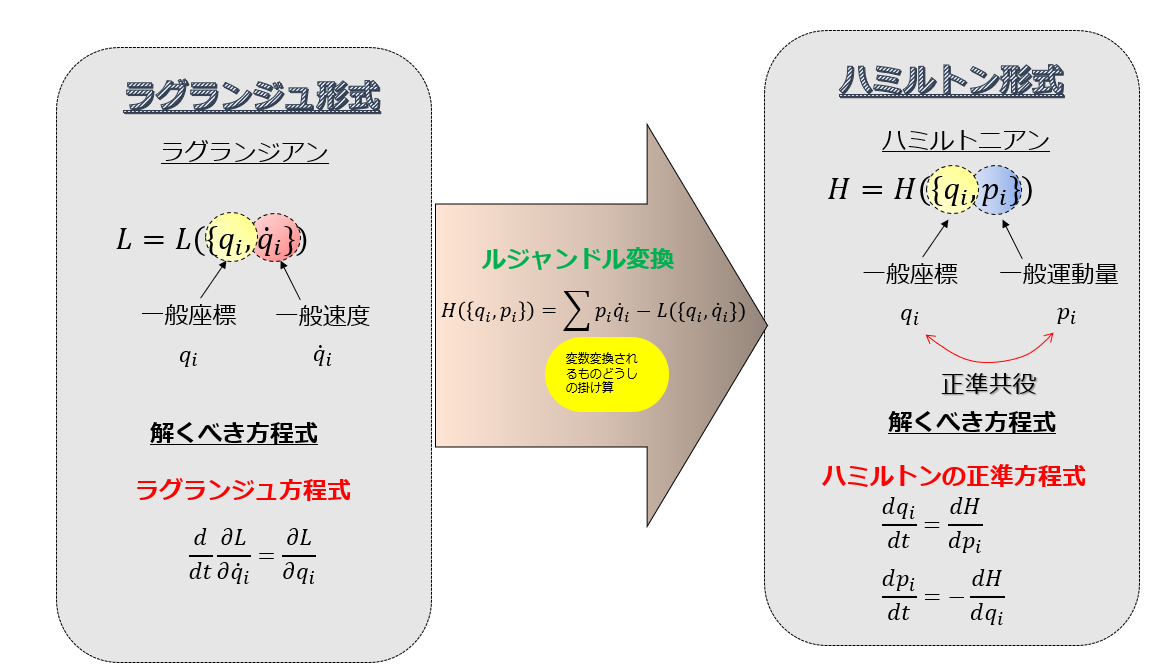
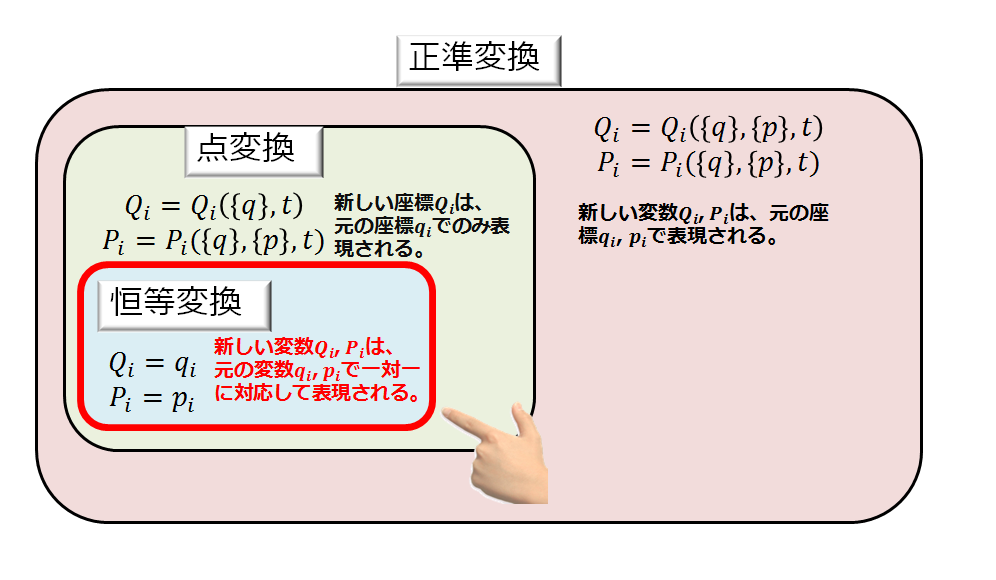
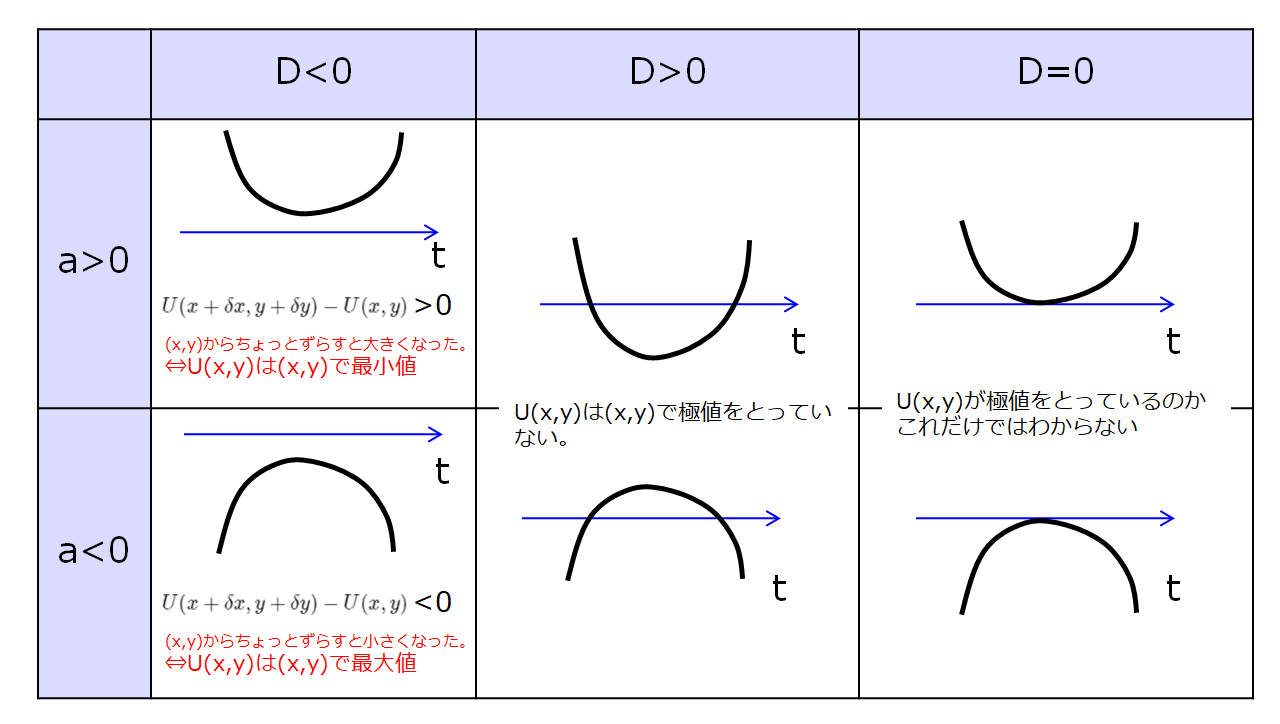
こんにちは(@t_kun_kamakiri)(^^)/
前回は、下記のように「ラグランジュ未定乗数法」の例題演習を通じて、ある拘束条件のもと、ある関数が最小になる方法について解説しました。
前回の記事で何をしたかったからかと言いますと、
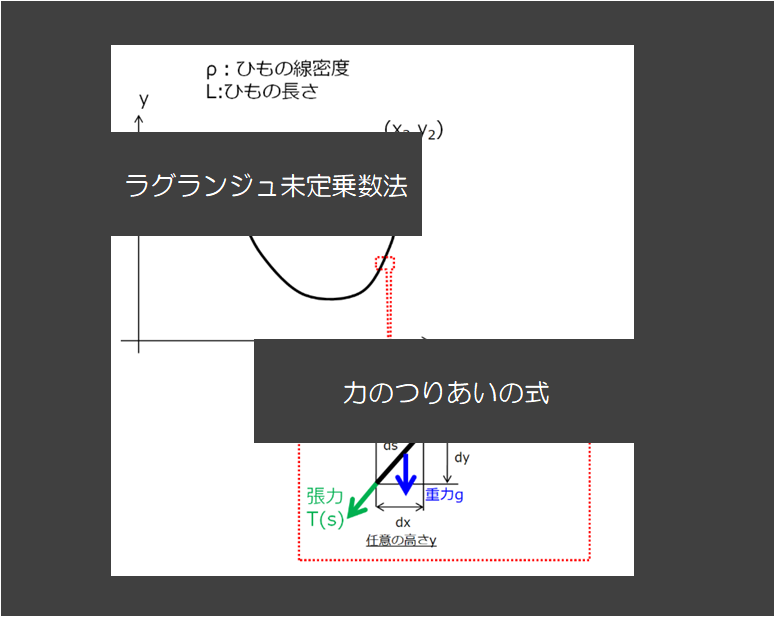
↑これを示したかったのです。
「運動方程式」or「力のつり合い」の式なのではないか?をいきなりは示すことができなさそうなので、まずは、
「ある関数\(U(x,y)\)がある拘束条件\(g(x,y)=0\)もとで最小となる場合を考える」とどのような状態が実現するかということから始めましょう。
問題
問題
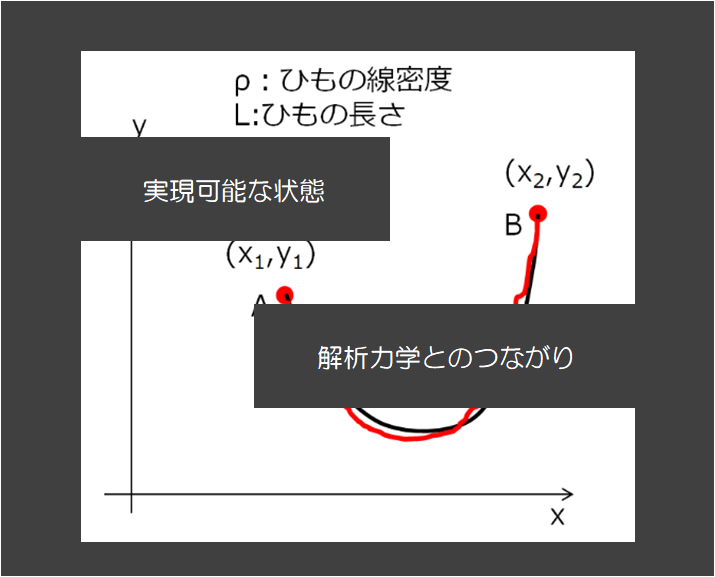
下の絵のように重力が働いている状態で、両端が固定された糸のつり合いを考えます。
どのような状態が実現するでしょうか(どのような糸の形になるでしょうか?)
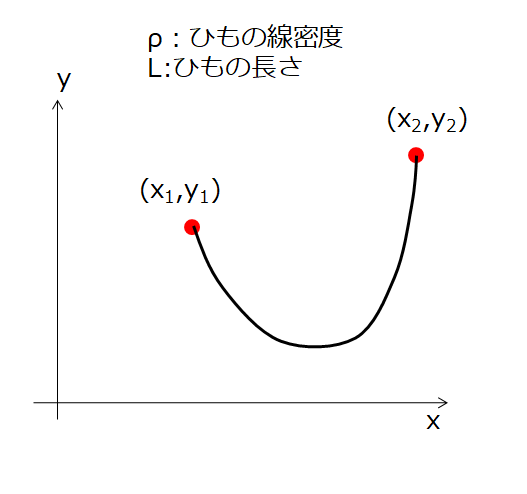
こんな感じの問題ですね~!(^^)!
上の「ラグランジュ未定乗数法」に置き換えて問題提起をしてみましょう!!
「ある関数\(U(x,y)\)がある拘束条件\(g(x,y)=0\)もとで最小となる」状態はどのような状態か?
↓
ひもが伸びたり縮んだりしない(ひもの長さ一定)という拘束条件のもと、ポテンシャル\(U(x,y)\)が最小になる状態はどのような状態か?
こんな感じに置き換えることができますね。
そしたら素直に、まずはポテンシャル\(U(x,y)\)とひもの長さ\(L\)を式で表現すれば良いということになります。
ポテンシャルエネルギーの式
ポテンシャルエネルギーってだいたいなんだ?ってお話ですが、この場合は重力ですね。
※どうしてポテンシャルなの?普通のエネルギーと何が違うの?と思った方は各自調べてみましょう(^^)
簡単言ったら、「力を\(\bf{F}=-\bf{\nabla}U\)と書けるとき、それをポテンシャルエネルギーという」ってとこでしょうか
ただこの場合のポテンシャルエネルギーの表現は難しい。。。
考える手順としては、微小区間に区切ってそれを積分すればよいのです。
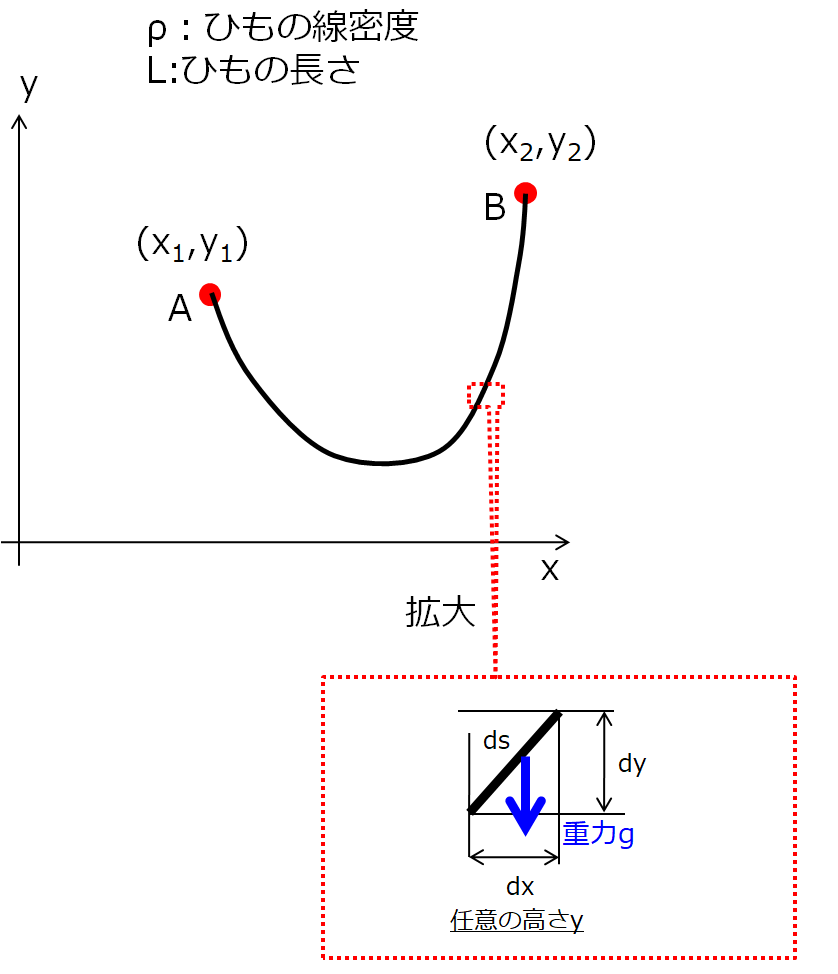
ほー、こう考えると、
微小区間の質量は、
ってことで、重力で\(\rho g ds\)で下に引っ張っているということですね。
任意の位置\(y\)でのポテンシャルエネルギーを考えているので、微小区間のポテンシャルエネルギーは、
であります。
それを区間AからBまで積分すればポテンシャルエネルギーは完成です!!
・・・
これでも\(ds\)がちょっと扱いづらいですね。
としてみましょうか。
なので、ポテンシャルエネルギーは、
となりました!(^^)!
ひもの長さが一定(拘束条件)
続いてひもの長さの計算です。
そういえば上の絵で微小区間の長さが、\(ds=\sqrt{dx^2+dy^2}\)でありましたね。
ってことは、全体のひもの長さは区間全体で積分してやれば、
・・・
これでもちょっと扱いづらいので、
とひもの長さの式が完成しました!(^^)!
変分:ちょっとずらした場合を考えよう
ラグランジュ未定乗数法を適用することを考えていくわけですが、
その前に、
(2)式を\(g(x,y)=L-\int_{A}^{B}\sqrt{1+\frac{dx}{dy}}dy\)とおきましょうかね。
そしたら\(g(x,y)=0\)が(2)式と等価な拘束条件となります。
とここで、
となっていたのですが、これでも少し扱いずらいなと感じました(僕の実力不足なのかもしれませんが・・・)
そこで、上記を導くのに「仮想変位\(\delta x\)、\(\delta y\)を与えた時、\(U\)の変化は0」という考えのもと導いたのですから原点に立ち返って考えた方が良さそうです。
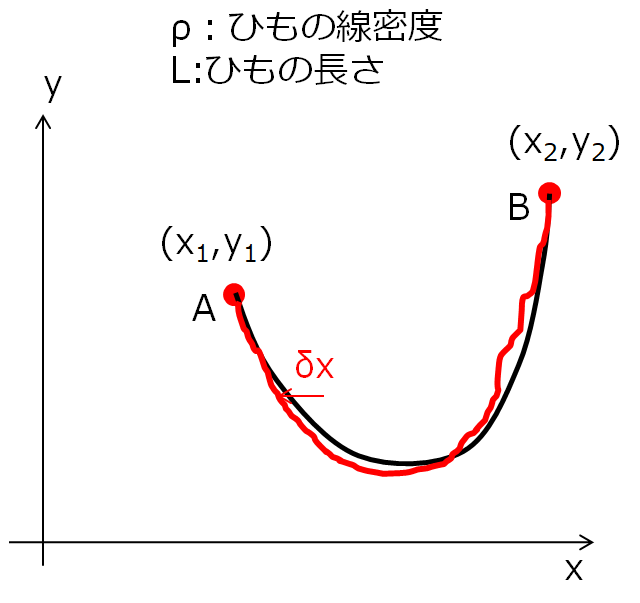
はい、\(\delta x\)だけずらしました(絵がガタガタですが、まあ良いでしょう)
※同じ高さyについて、x方向にちょっとずらしています。高さ方向にひもを持ち上げたら明らかに長さが変わってしまいます。ここで考えているのは「つり合いが取れいる状態のときひもはどんな形状になっているか?」であるため、つり合いがとれた状態で仮想的にちょっとずらすというのがポイントになります。ですので、\(\delta y\)については時に考えなくても良いでしょう。
そして、
ポテンシャルについても、ひもの長さ(今の場合はg(x,y))について仮想変位\(delta x\)について、
となっているはずです。つり合いが取れているのであれば・・・
ただよく見ると、\(U\)や\(g\)には、\(x\)ではなく\(\frac{dx}{dy}\)が入っていますね。
そうは言っても結局、
※\(\frac{dx}{dy}=x^{\prime}\)
として(3),(4)式は、
同様に、\(g(x,y)\)についてもやりましょう。
ラグランジュ未定乗数法の適用
ようやく下準備ができました!(^^)!
あとはラグランジュ未定乗数法に従って、
\(g(x,y)=0\)の条件のもと、\(\delta U+\lambda \delta g=0\)を解けば、
糸が釣り合っている場合の実現しうる状態というのが求まりそうです。
そしたら、(7),(8)式を\(\lambda\)を使って・・・
こうなりました。
あとは、これを腕力でゴリゴリ解いていくわけです・・・・・・・・と言ってもたいしたことありません(笑)
(左辺) =
なので、\(\frac{d(\delta x)}{dy}\)に着目して部分積分をします。
そうすると(9)式が、
になりました(^^)
そして、A点とB点は固定してありますので動かせませんので、そこでの\(\delta x=0\)ですね。
ということは、(10)式の第一項は消えてしまいます。
それから、第二項についてはどんな仮想変位\(\delta x\)に対して恒等的に成り立つのですから、
となっているはずです。・・・・
ふ~ちょっと休憩・・・・(´・ω・`)
あとは腕力にものを言わせてゴリゴリ解きます
休憩が終わりました(休憩してから2時間経っています。)

ゴリゴリ(ウホウホ)解きます。
を解くのですが、
\(x^{\prime}=\frac{dx}{dy}\)を求めて、ここから\(x\)と\(y\)の関係を導けば、
それが「糸がつり合いをとれている状態での形状」ということになります。
と、このように定数とおけます。
したがって、これは、
と、こうなりました。
両辺、\(y\)で積分しましょう。
左辺は、\(x\)となるのが明らかですね。
右辺のプラスマイナス(\(\pm\))が邪魔なので、\(a\)にプラスマイナス(\(\pm\))も含めてしまいましょう。
ここからは微分積分のお話ですね。
さらっと書いておきますと・・・\(y+\lambda=a\cosh\theta\)とおくと上手くいきます。
5年ぶりにすると、これどうやるんだったっけか?ってちょい苦戦しました(笑)

※誰かのヒントになればと思っています
(あれ?違う・・・こうか・・・あれ?ってしている間にこんなぐちゃぐちゃになりました)
やりました(^^)/
「糸がつり合いをとれている状態での形状」とは、\(y=a\cosh\big(\frac{x-b}{a}-\lambda\big)\)
となりました。\(x\)と\(y\)の関係が出ました。
これが答えですね。
とことで、定数\(a\)、\(b\)、\(\lambda\)ですが、これらは下記の3つの条件で求まります。
- (1)\(g(x,y)=0\)
- (2)A点で拘束
- (3)B点で拘束
未知数3つ、条件3つなので原理的には定数\(a\)、\(b\)、\(\lambda\)は決まりますね。
原理的にですが・・・めんどうなのでやりません(笑)
まとめ
この考えのもと、
「糸がつり合いをとれている状態での形状」とは、\(y=a\cosh\big(\frac{x-b}{a}-\lambda\big)\)
と求めました。
次回
いよいよ下記の僕の仮説に迫ります!(^^)!
本例題を用いてやってみます。
今回の例題では、運動方程式ではなく力のつり合いに該当します。
「力のつり合いに値するのではないか?」の部分は本例題の中でいうと、
↑これです。
本例題を「ラグランジュ未定乗数法」ではなくて、
力のつり合いから純粋に考えて(11)式になってくれないといけない・・・とこのように思うわけです。
なので次回は、本例題を力のつり合いから考えて、(11)式が導けるか確認してみましょう(^^)/
できるかな(笑)
ちなみに・・・・
ちなみにこの例題は僕独自の例題ではないです。。。
こちらの例題を眺めていたら、たまたま見つかったので、利用させていただいております。
P.227ですね。。
ただ、僕の説明の方が絶対わかりやすいです。(回りくどいかもしれませんが・・)
参考図書
いくつかおすすめの解析力学の参考書を挙げておきます。
ランダウ力学
下記のような小教程もあります。
解析力学:マセマキャンパスゼミ
↑こちらは「スバラシク実力がつくと評判」シリーズの解析力学の参考書です。
著者は高校数学を教える予備校の講師で、とてもわかりやすいと評判です。
その方が書いた書籍なので高校生でも読みこなすことができるくらいわかりやすく、かつちゃんと大学の物理の内容を扱っています。
解析力学ⅠⅡ:朝倉物理学大系
この2冊は解析力学の名著ですね。
数学的な解説も多く、解析力学を深く学ぶ人には挑戦するには申し分ない内容です。