前回、正準変換の記事を書きました。
前回の記事はこちら
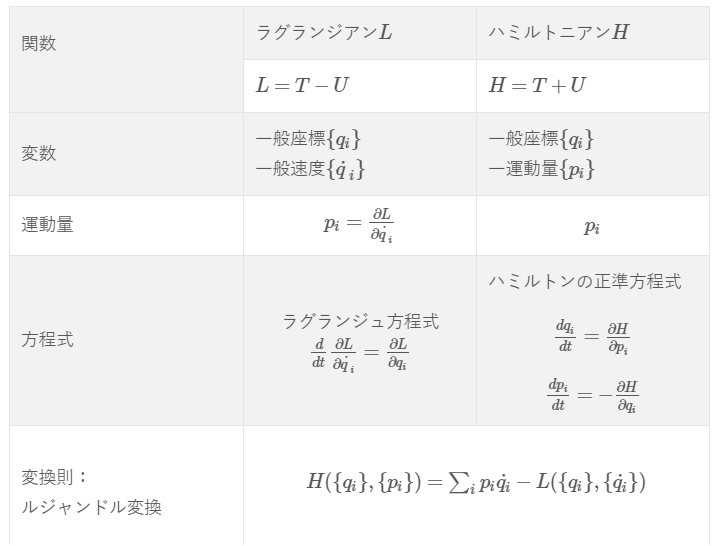
正準変換で、元の変数\(\{q_{i}\},\{p_{i}\}\)からハミルトンの正準方程式を満たすように新しい変数\(\{Q_{i}\},\{P_{i}\}\)へ変換する際、母関数というのを導入しました。
こんな感じです。
\begin{align*}p_{i}=\frac{\partial W_{1}}{\partial q_{i}}\cdot\cdot\cdot (1)\end{align*}
\begin{align*}P_{i}=-\frac{\partial W_{1}}{\partial Q_{i}}\cdot\cdot\cdot (2)\end{align*}
\begin{align*}{H}’=H+\frac{\partial W_{1}}{\partial t}\cdot\cdot\cdot (3)\end{align*}
関数\(W_{1}\)が母関数です。
正準変換は、この母関数によって特徴づけられるためとても重要です。
母関数\(F\)の変数は何かと言いますと、\(\{q_{i}\}\)と\(\{Q_{i}\}\)と選びました。
しかし、何も変数を\(\{q_{i}\}\)と\(\{Q_{i}\}\)とで表さずにルジャンドル変換を上手く使えば、変数は変えることができるのです。
そこで↓
本記事
変数を\(\{q_{i}\}\)と\(\{Q_{i}\}\)を変数と選びしたが、ルジャンドル変換を使えば自在に変数を変えることができます!(^^)!
今は\(W_{1}(\{q_{i}\},\{Q_{i}\})\)ですが、これを
\(W_{1}(\{q_{i}\},\{Q_{i}\})\)
↓\(\{Q_{i}\}\)→\(\{P_{i}\}\)
\(W_{2}(\{q_{i}\},\{P_{i})\}\)
↓\(\{q_{i}\}\)→\(\{p_{i}\}\)
\(W_{3}(\{p_{i}\},\{P_{i}\})\)
↓\(\{P_{i}\}\)→\(\{Q_{i}\}\)
\(W_{4}(\{p_{i}\},\{Q_{i}\})\)
つまり、元の変数\(\{q_{i}\}\)と\(\{p_{i}\}\)から一組選び、新しい変数\(\{Q_{i}\}\)と\(\{P_{i}\}\)から一組選ぶ方法の合計4パターンの変数の選び方があることを示す。
全てバカ正直に示しても良いですが、ひとつやり方だけ紹介して、後は結果だけ示して終わりにします。
この記事では、
\begin{align*}W_{1}(\{q_{i}\},\{Q_{i}\})\end{align*}
↓\(\{Q_{i}\}\)→\(\{P_{i}\}\)
\begin{align*}W_{2}(\{q_{i}\},\{P_{i}\})\end{align*}
↑この変換を示します(^^)/
要するに変数を\(\{q_{i}\}\)と\(\{P_{i}\}\)にしたいのです。
母関数の変数を変換する
変数が\(\{q_{i}\}\)と\(\{P_{i}\}\)とした場合の母関数
前回の記事の⑬式からスタートすることになります。
前回の記事はこちら
(13)式を\(dt\)を書けて全微分の形にしておきます。
\begin{align*}dW_{1}=\sum_{i}p_{i}dq_{i}+\sum_{i}(-P_{i})dQ_{i}+({H}’-H)dt\cdot\cdot\cdot (4)\end{align*}
ここで、右辺第二項について、
\begin{align*}d(P_{i}Q_{i})=P_{i}dQ_{i}+Q_{i}dP_{i}\cdot\cdot\cdot (5)\end{align*}
ということに着目すると、(4)式は
\begin{align*}dW_{1}=\sum_{i}p_{i}dq_{i}+\sum_{i}\big(-d(P_{i}Q_{i})+Q_{i}dP_{i}\big)+({H}’-H)dt\cdot\cdot\cdot (6)\end{align*}
⇔
\begin{align*}d(W_{1}+\sum_{i}P_{i}Q_{i})=\sum_{i}p_{i}dq_{i}+\sum_{i}Q_{i}dP_{i}+({H}’-H)dt\cdot\cdot\cdot (7)\end{align*}
これを見ると、
\begin{align*}W_{2}=W_{1}+\sum_{i}P_{i}Q_{i}\cdot\cdot\cdot (8)\end{align*}
と置けば、ルジャンドル変換をしていることになります。
「ルジャンドル変換」の記事はこちら
ここで、\(G\)変数を変数を\(\{q_{i}\}\)と\(\{P_{i}\}\)と見れば、
\begin{align*}dW_{2}=\sum_{i}\frac{\partial W_{2}}{\partial q_{i}}dq_{i}+\sum_{i}\frac{\partial W_{2}}{\partial P_{i}}dP_{i}+\frac{\partial W_{2}}{\partial t}dt\cdot\cdot\cdot (9)\end{align*}
となります。※時間も陽に依存
(7)と(9)を比較します。
\begin{align*}p_{i}=\frac{\partial W_{2}}{\partial q_{i}}\cdot\cdot\cdot (10)\end{align*}
\begin{align*}Q_{i}=\frac{\partial W_{2}}{\partial P_{i}}\cdot\cdot\cdot (11)\end{align*}
\begin{align*}{H}’=H+\frac{\partial W_{2}}{\partial t}\cdot\cdot\cdot (12)\end{align*}
\begin{align*}W_{2}=W_{1}+\sum_{i}P_{i}Q_{i}\cdot\cdot\cdot (8)\end{align*}
↑これが変数変数を\(\{q_{i}\}\)と\(\{P_{i}\}\)とした場合の母関数である。
同じようになやり方をすれば、変数は元の変数\(\{q_{i}\}\)と\(\{p_{i}\}\)から一組選び、新しい変数\(\{Q_{i}\}\)と\(\{P_{i}\}\)から一組選ぶ方法の合計4パターン作ることできる。
もう2パターン示したことになります。
後の2パターンは、結果を示します。
結果:同じようにして変数を変換
変数が\(\{p_{i}\}\)と\(\{P_{i}\}\)とした場合の母関数
\begin{align*}W_{2}(\{q_{i}\},\{P_{i})\}\end{align*}
↓\(\{q_{i}\}\)→\(\{p_{i}\}\)
\begin{align*}W_{3}(\{p_{i}\},\{P_{i}\})\end{align*}
\begin{align*}W_{3}=W_{2}-\sum_{i}p_{i}q_{i}\cdot\cdot\cdot (13)\end{align*}
\begin{align*}q_{i}=-\frac{\partial W_{3}}{\partial p_{i}}\cdot\cdot\cdot (14)\end{align*}
\begin{align*}Q_{i}=\frac{\partial W_{3}}{\partial P_{i}}\cdot\cdot\cdot (15)\end{align*}
\begin{align*}{H}’=H+\frac{\partial W_{3}}{\partial t}\cdot\cdot\cdot (16)\end{align*}
変数が\(\{p_{i}\}\)と\(\{Q_{i}\}\)とした場合の母関数
\begin{align*}W_{3}(\{p_{i}\},\{P_{i}\})\end{align*}
↓\(\{P_{i}\}\)→\(\{Q_{i}\}\)
\begin{align*}W_{4}(\{p_{i}\},\{Q_{i}\})\end{align*}
\begin{align*}W_{4}=W_{3}-\sum_{i}P_{i}Q_{i}\cdot\cdot\cdot (17)\end{align*}
\begin{align*}q_{i}=-\frac{\partial W_{4}}{\partial p_{i}}\cdot\cdot\cdot (18)\end{align*}
\begin{align*}P_{i}=-\frac{\partial W_{4}}{\partial Q_{i}}\cdot\cdot\cdot (19)\end{align*}
\begin{align*}{H}’=H+\frac{\partial W_{4}}{\partial t}\cdot\cdot\cdot (20)\end{align*}
まとめ
本記事で示したように、母関数に関して元の変数\(\{q_{i}\}\)と\(\{p_{i}\}\)から一組選び、新しい変数\(\{Q_{i}\}\)と\(\{P_{i}\}\)から一組選ぶことで、ひとつの正準変換を可能にします。
このように母関数の定めると、ひとつの正準変換を産み出すという意味で、母みたいな関数です(笑)
英語だと”generating function”なので、”産み出す関数”と言う意味です。