解析力学

ルジャンドル変換からハミルトンの正準方程式の導出

どうも(^^)/

前回ルジャンドル変換を勉強して自分なりにまとめました。

なんかもっと解析力学で出てくるような問題を扱うにあたって実用的なである方が良いと思ったので、表にまとめてみました。

 

表の中身の導出は次回にするとして、結果だけまとめて頭に入れておきたいところです(^^)

スポンサーリンク

 

目次
  1. ルジャンドル変換：表にまとめた
    1. 解析力学へ適用
  2. ルジャンドル変換からハミルトンの正準方程式へ
    1. (6)式について
    2. (7)式について
  3. まとめ
  4. 次回

ルジャンドル変換：表にまとめた

 

\(\{a_{i}\}\)、\(\{b_{i}\}\)、\(\{c_{i}\}\)は互いに独立な変数たちとします。

ある関数\(f(\{c_{i}\},\{a_{i}\})\)から別の変数を持った関数\(g(\{c_{i}\},\{b_{i}\})\)に変換する。
※変数の集合\({c_{i}}\)は共通

\begin{align*}g(\{c_{i}\},\{b_{i}\})=\sum_{i}a_{i}b_{i}-f(\{a_{i}\},\{b_{i}\})\end{align*}
（すっきり書くと\(g=\sum_{i}a_{i}b_{i}-f\)）

↑これがルジャンドル変換です。

 

表にまとめましょう(^^)/

関数 \(f\) \(g\)
互いに独立な変数

\(f\)の変数
\(\{c_{i}\},\{a_{i}\}\)

※\(a_{i}=\frac{\partial g}{\partial b_{i}}\)
↑これが成り立つとする

\(g\)の変数
\(\{c_{i}\},\{b_{i}\}\)

※\(b_{i}=\frac{\partial f}{\partial a_{i}}\)
↑これが成り立つとする
共通の変数 \(\{c_{i}\}\)
ルジャンドル変換

\(g(\{c_{i}\},\{b_{i}\})=\sum_{i}a_{i}b_{i}-f(\{a_{i}\},\{b_{i}\})\)

「別の関数」=「共通していない変数同士の積の和」ー「元の関数」
ルジャンドル変換からの産物

\(\frac{\partial f}{\partial c_{i}}=-\frac{\partial f}{\partial c_{i}}\)

「元の関数の\(c_{i}\)の偏微分」＝－「別の関数の\(c_{i}\)の偏微分」

 

解析力学へ適用

 

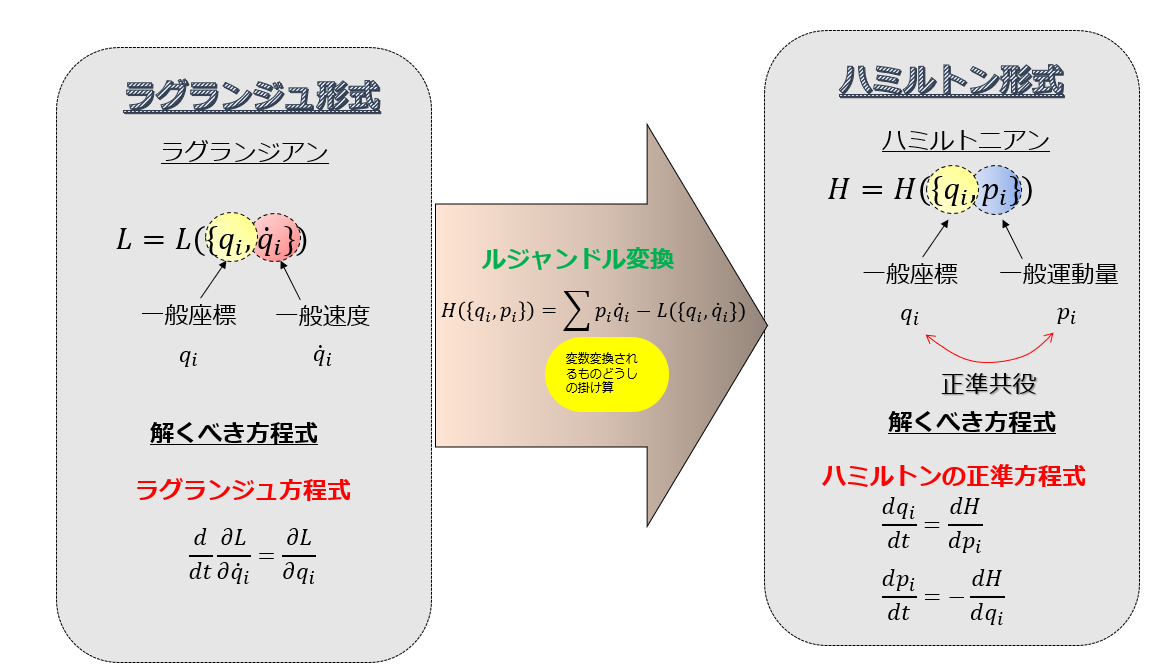
上の表を解析力学に適用してみます。

「ラグランジアン\(L\)は一般座標\(q_{i}\)と一般速度\(\dot{q_{i}}\)の変数」

↓

「ハミルトン\(H\)：一般座標\(q_{i}\)と一般運動量\(\dot{q_{i}}\)の変数」に変換

 

上述の表に対してこのような対応付けで見てみましょう♪

関数
\(f\)→\(L\)
\(g\)→\(H\)

変数
\(a_{i}\)→\(\dot{q_{i}}\)：一般速度
\(b_{i}\)→\(p_{i}\)：一般運動量
\(c_{i}\)→\(q_{i}\)：一般座標（\(L\)と\(H\)で共通の変数）

 

そうすると下記のような表になります。

関数 \(L\) \(H\)
互いに独立な変数

\(L\)の変数
\(\{q_{i}\},\{\dot{q_{i}}\}\)

※\(\dot{q_{i}}=\frac{\partial H}{\partial p_{i}}\)・・・①
↑これが成り立つとする

\(H\)の変数
\(\{q_{i}\},\{p_{i}\}\)

※\(p_{i}=\frac{\partial L}{\partial \dot{q_{i}}}\)・・・②
↑これが成り立つとする
これについては「運動量保存」のところで記事を書きました。
共通の変数 \(\{q_{i}\}\)
ルジャンドル変換

\(H(\{q_{i}\},\{p_{i}\})=\sum_{i}p_{i}\dot{q_{i}}-L(\{q_{i}\},\{\dot{q_{i}}\})\)
・・・③

「別の関数」=「共通していない変数同士の積の和」ー「元の関数」
ルジャンドル変換からの産物

\(\frac{\partial L}{\partial q_{i}}=-\frac{\partial H}{\partial q_{i}}\)・・・④

「元の関数の\(q_{i}\)の偏微分」＝－「別の関数の\(q_{i}\)の偏微分」

さらに解析力学の場合は、ラグランジュ方程式もあります。

\begin{align*}\frac{d}{dt}\frac{\partial L}{\partial \dot{q_{i}}}=\frac{\partial L}{\partial q_{i}}\cdot\cdot\cdot (5)\end{align*}

 

ルジャンドル変換からハミルトンの正準方程式へ

 

さて、道具がそろったような気持ちでいます。

上述の表（ルジャンドル変換）とラグランジュ方程式を使ってハミルトンの正準方程式を導きます。

ハミルトンの正準方程式

ハミルトニアン\(H(\{q_{i}\},\{p_{i}\})\)に対して

\begin{align*}\frac{dq_{i}}{dt}=\frac{\partial H}{\partial p_{i}}\cdot\cdot\cdot (6)\end{align*}

\begin{align*}\frac{dp_{i}}{dt}=-\frac{\partial H}{\partial q_{i}}\cdot\cdot\cdot (7)\end{align*}

が成立する。

このようなとても対称性の良い方程式がハミルトンの正準方程式です。

では、(6)(7)式を導出しましょう(^^)/

とっても簡単です(笑)

(6)式について

 

(6)式は(1)式でそのまま成り立っていますね(^^)

\begin{align*}
\frac{d q_{i}}{dt}=\frac{\partial H}{\partial p_{i}}\cdot\cdot\cdot (6)\end{align*}

(7)式について

 

まず、(4)式

\begin{align*}\frac{\partial L}{\partial q_{i}}=-\frac{\partial H}{\partial q_{i}}\cdot\cdot\cdot (4)\end{align*}


の左辺に対して(5)式（ラグランジュ方程式）を適用します。

すると、

\begin{align*}\frac{d}{dt}\frac{\partial L}{\partial \dot{q_{i}}}=-\frac{\partial H}{\partial q_{i}}\end{align*}

となります。

そしたらこの左辺に②式を適用させましょう。

\begin{align*}\frac{dp_{i}}{dt}=-\frac{\partial H}{\partial q_{i}}\cdot\cdot\cdot (7)\end{align*}

 

まとめ

 

お気づきのことでしょう。

(3)式で下記のようにラグランジアン\(L(\{q_{i}\},\{\dot{q_{i}}\})\)をハミルトニアン\(H(\{q_{i}\},\{\dot{p_{i}}\})\)へ変換しましたね。

\begin{align*}H(\{q_{i}\},\{p_{i}\})=\sum_{i}p_{i}\dot{q_{i}}-L(\{q_{i}\},\{\dot{q_{i}}\})\cdot\cdot\cdot (3)\end{align*}

その時に、

\begin{align*}\dot{q_{i}}=\frac{\partial H}{\partial p_{i}}\cdot\cdot\cdot (1)\end{align*}

\begin{align*}p_{i}=\frac{\partial L}{\partial \dot{q_{i}}}\cdot\cdot\cdot (2)\end{align*}

が成り立つものとしていました。

 

そして、上記の式とラグランジュ方程式を使って、ハミルトンの正準方程式⑥⑦式を導出しました。

\begin{align*}\frac{dq_{i}}{dt}=\frac{\partial H}{\partial p_{i}}\cdot\cdot\cdot (6)\end{align*}

\begin{align*}\frac{dp_{i}}{dt}=-\frac{\partial H}{\partial q_{i}}\cdot\cdot\cdot (7)\end{align*}

ということは、
「ラグランジュ方程式」と「ハミルトンの正準方程式」は等価なものと言えます。

 

一般座標と一般速度を用いた際に、ラグランジアン\(L\)さえ決まれば、ラグランジュ方程式から運動方程式が導けました。

それと同じでハミルトニアンさえわかっていれば、ハミルトンの正準方程式から運動方程式がわかると言えます。

しかもとっても対称性の良い！！

たぶんもっとこのハミルトンの正準方程式の形にする旨みがあるはずです（僕の勉強不足か・・・）

きっと正準変換とか勉強すれば、もう少し見通しがよくなることでしょう(笑)

 

次回

 

この記事でいきなりルジャンドル変換を表にまとめたりしました(笑)

せめて、

\begin{align*}H(\{q_{i}\},\{p_{i}\})=\sum_{i}p_{i}\dot{q_{i}}-L(\{q_{i}\},\{\dot{q_{i}}\})\cdot\cdot\cdot (3)\end{align*}

の導出はしておきたいです(‘;’)

関連記事もどうぞ

COMMENT

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です