ルジャンドル変換の導出：超簡単に導出

どうも(^^)/

前々回にルジャンドル変換を絵でイメージできるように頑張って記事を書いたんですよね。

でも正直まだ理解できていません(笑)

だったら、表にまとめて覚えておくだけでもいいんじゃないかと思って、前回は下記のブログで「さくっ」っと表にまとめて、頭の中を整理したのです(‘;’)

「さくっ」っとまとめたのですが、やっぱり「ルジャンドル変換」を導いておきたいと・・・・そんな欲が出たので、

本日はルジャンドル変換をこれまた「さくっ」っと今度は数式で導きたいと思います(^^)/

ルジャンドル変換まとめ
ルジャンドル変換の導出
なんか(9)式に定数分ついちゃったけど・・・
まとめ
参考図書

ルジャンドル変換まとめ

\(\{a_{i}\}\)、\(\{b_{i}\}\)、\(\{c_{i}\}\)は互いに独立な変数たちとします。

ある関数\(f(\{c_{i}\},\{a_{i}\})\)から別の変数を持った関数\(g(\{c_{i}\},\{b_{i}\})\)に変換する。
※変数の集合\({c_{i}}\)は共通

\begin{align*}g(\{c_{i}\},\{b_{i}\})=\sum_{i}a_{i}b_{i}-f(\{a_{i}\},\{b_{i}\})\cdot\cdot\cdot (1)\end{align*}

（すっきり書くと\(g=\sum_{i}a_{i}b_{i}-f\)）

↑これがルジャンドル変換です。

関数	\(f\)	\(g\)
互いに独立な変数	\(f\)の変数 \(\{c_{i}\},\{a_{i}\}\) ※\(a_{i}=\frac{\partial g}{\partial b_{i}}\)・・・② ↑これが成り立つとする	\(g\)の変数 \(\{c_{i}\},\{b_{i}\}\) ※\(b_{i}=\frac{\partial f}{\partial a_{i}}\)・・・③ ↑これが成り立つとする
共通の変数	\(\{c_{i}\}\)
ルジャンドル変換	\(g(\{c_{i}\},\{b_{i}\})=\sum_{i}a_{i}b_{i}-f(\{a_{i}\},\{b_{i}\})\)・・・① 「別の関数」=「共通していない変数同士の積の和」ー「元の関数」
ルジャンドル変換からの産物	\(\frac{\partial f}{\partial c_{i}}=-\frac{\partial f}{\partial c_{i}}\)・・・④ 「元の関数の\(c_{i}\)の偏微分」＝－「別の関数の\(c_{i}\)の偏微分」

ルジャンドル変換の導出

\(\{a_{i}\}\)、\(\{b_{i}\}\)、\(\{c_{i}\}\)がちょびっと動いたときの関数\(f\)と\(g\)の変化量を見てみます。

変分ですね。

変分の計算は散々やりましたので、↓こちらを参考に
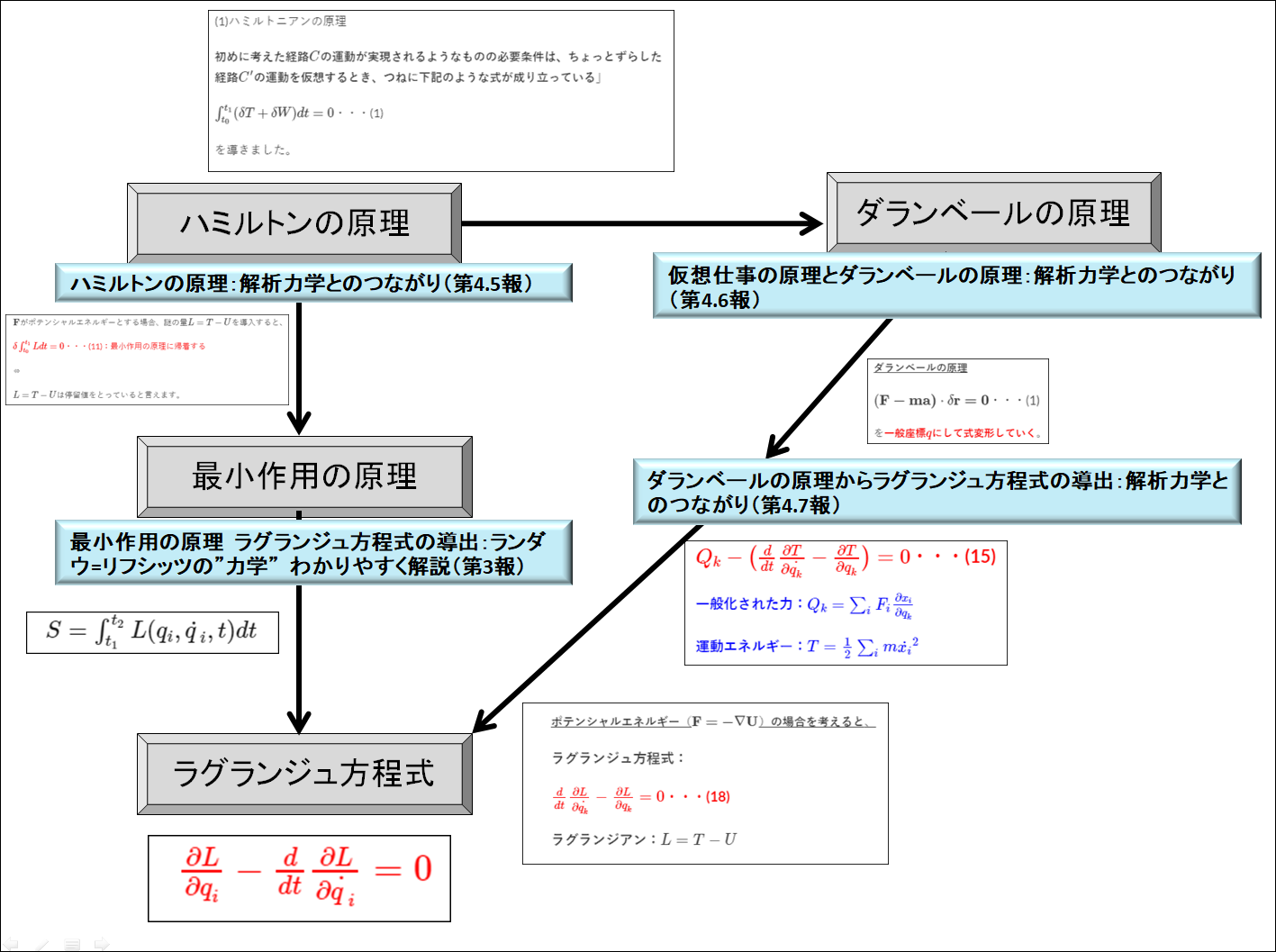
最小作用の原理　ラグランジュ方程式の導出：ランダウ=リフシッツの”力学”　わかりやすく解説（第3報）

\begin{align*}delta f=\sum_{i}\frac{\partial f}{\partial a_{i}}\delta a_{i}+\sum_{i}\frac{\partial f}{\partial c_{i}}\delta c_{i}\cdot\cdot\cdot (5)\end{align*}

\begin{align*}\delta g=\sum_{i}\frac{\partial g}{\partial b_{i}}\delta b_{i}+\sum_{i}\frac{\partial g}{\partial c_{i}}\delta c_{i}\cdot\cdot\cdot (6)\end{align*}

そして、(5)＋(6)をします。

\begin{align*}\delta (f+g)=\sum_{i}(\frac{\partial f}{\partial a_{i}}\delta a_{i}+\frac{\partial g}{\partial b_{i}}\delta b_{i})+\sum_{i}(\frac{\partial f}{\partial c_{i}}+\frac{\partial g}{\partial c_{i}})\delta c_{i}\end{align*}

ここで②③式を使うと右辺第一項がもうちょっとすっきりします。

\begin{align*}\delta (f+g)=\sum_{i}(b_{i}\delta a_{i}+a_{i}\delta b_{i})+\sum_{i}(\frac{\partial f}{\partial c_{i}}+\frac{\partial g}{\partial c_{i}})\delta c_{i}\cdot\cdot\cdot (7)\end{align*}

さらに右辺の第一項は、

\begin{align*}b_{i}\delta a_{i}+a_{i}\delta b_{i}=\delta(a_{i}b_{i})\end{align*}

と書けますね。

↑本当ですか？って思ったので、一応やってみます。
\(h(a_{i},b_{i})=a_{i}b_{i}\)と関数を用意します。
\(\delta h=\frac{\partial h}{\partial a_{i}}\delta a_{i}+\frac{\partial h}{\partial b_{i}}\delta b_{i}=b_{i}\delta a_{i}+a_{i}\delta b_{i}\)と、ま～あっさり導けましたね。
一応そうなることはわかるんですが、時々「本当か？」って思って確かめた方がいいですよね。

(7)式を全部左辺に集めます。

\begin{align*}\delta \big(f+g-\sum_{i}(a_{i}b_{i})\big)-\sum_{i}(\frac{\partial f}{\partial c_{i}}+\frac{\partial g}{\partial c_{i}})\delta c_{i}=0\cdot\cdot\cdot (8)\end{align*}

※左辺第三項目の∑とδも入れ替えましたけど、線形なのでま～大丈夫でしょう(笑)

これが、任意の\(a_{i}\)、\(b_{i}\)、\(c_{i}\)に対して成り立たないといけないので、

\begin{align*}f+g-\sum_{i}(a_{i}b_{i})=const\end{align*}

\begin{align*}\frac{\partial f}{\partial c_{i}}+\frac{\partial g}{\partial c_{i}}=0\end{align*}

⇔

\begin{align*}g=\sum_{i}(a_{i}b_{i})-f+(const)\cdot\cdot\cdot (9)\end{align*}

\begin{align*}\frac{\partial f}{\partial c_{i}}=-\frac{\partial g}{\partial c_{i}}\cdot\cdot\cdot (10)\end{align*}

出来ましたね(^^)/

なんか(9)式に定数分ついちゃったけど・・・

\begin{align*}g=\sum_{i}(a_{i}b_{i})-f+(const)\cdot\cdot\cdot (9)\end{align*}

(9)式に、こんな感じで定数が余分についてしまいました。

どうなんでしょう。

あまり定数が足させても本質の部分では問題ない気もしますが・・・

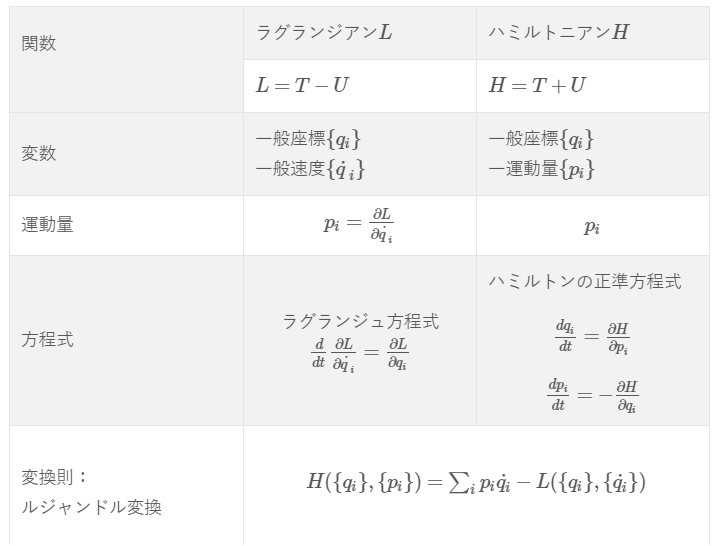
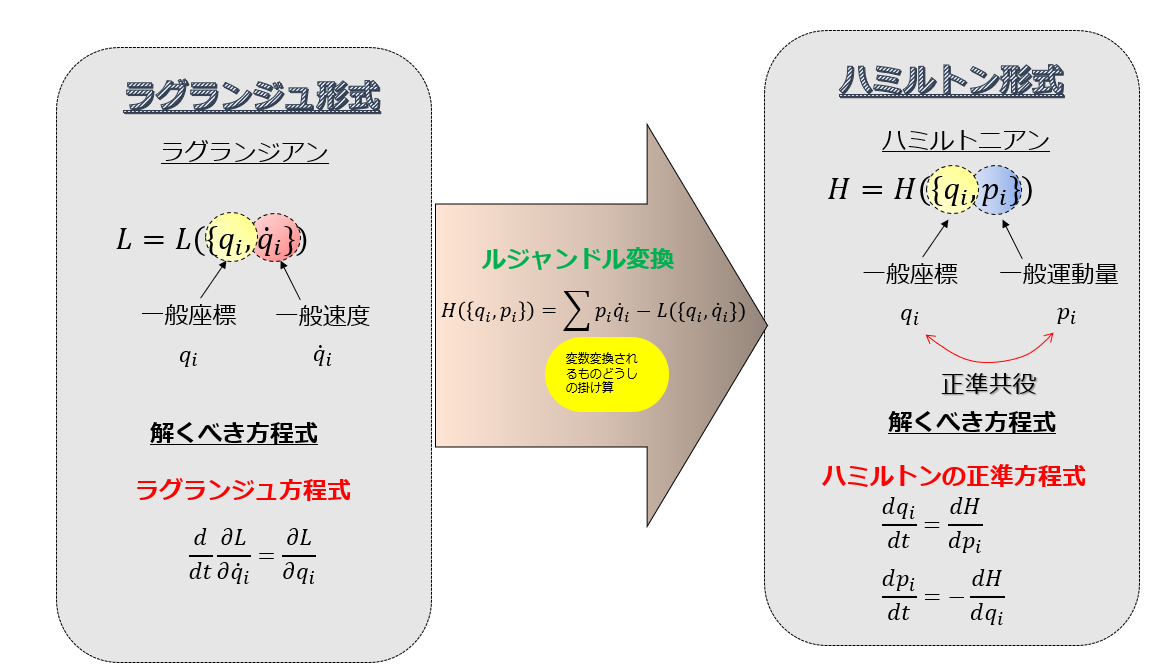
たとえば解析力学でルジャンドル変換と言えば、

\begin{align*}H(\{q_{i}\},\{p_{i}\})=\sum_{i}p_{i}\dot{q_{i}}-L(\{q_{i}\},\{\dot{q_{i}}\})\end{align*}

↓

これに定数分足します。

\begin{align*}H(\{q_{i}\},\{p_{i}\})=\sum_{i}p_{i}\dot{q_{i}}-L(\{q_{i}\},\{\dot{q_{i}}\})＋(const)\end{align*}

こんな感じですよね。

ハミルトニアン\(H\)はここではエネルギーなのですから、エネルギーの絶対的な大きさ何て意味がなかったはずです。

エネルギーは「ある基準からどれだけ大きいか」といった相対的な大きさに意味があるのでしたから、定数分ずらしたところで特に本質ではないと考えられます。

ルジャンドル変換には定数だけ任意性がある？

↓下記の記事で書いたとおりに、定数分ずらしてみましょう。
ルジャンドル変換：イメージ図と利用例を挙げてみた（第12.1）

\(f(x)\)から\(g(p)\)(※\(p=\frac{df}{dx}\)）への変換は、\(f\)に対する接線を考えたときのy切片を\(g(p)\)と置いて変換の手続きをするのでしたね。
では、\(g\)を定数＝cだけずらしてみましょう。

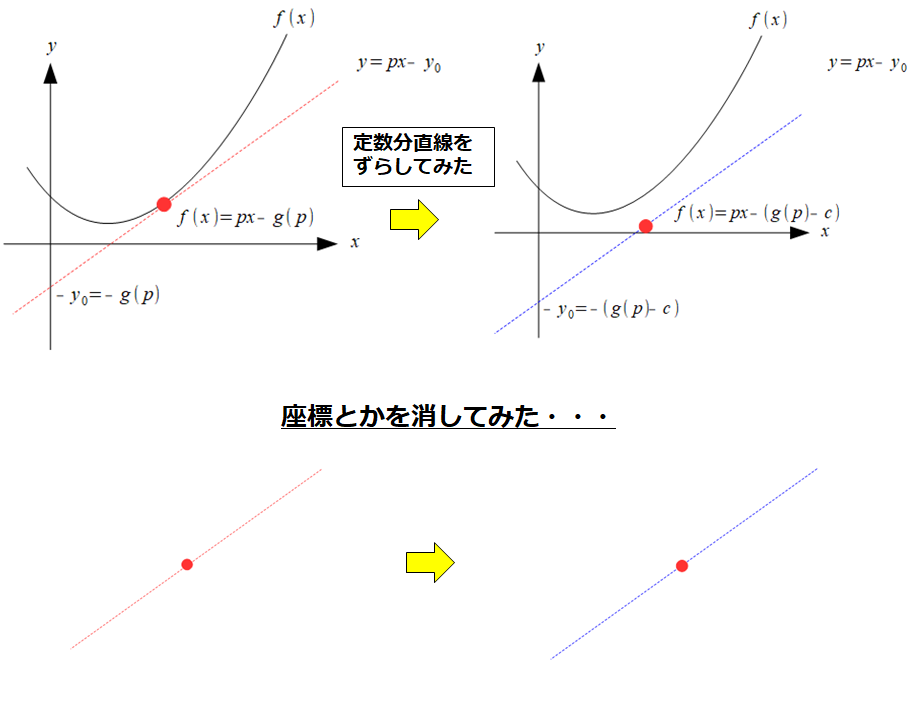
そうすると確かに、見た目の関係が変わりましたね。

でも全部座標やらを消してみて\(g\)に関係している直線だけ残しました。

するとどうだ・・・・

区別がつかない(笑)

と、ま～雑な議論だけども、一応納得しましょう(笑)

エネルギーなんて単体の絶対的な大きさを比較することもないってことでも納得できるのでしょうかね。

実際は、エネルギーの変化量（この時点で定数はどうでもよくなる）や別のエネルギー量と比較したりしますしね。

それで、別のエネルギー量どうしを比較するときも「基準が同じであるときのエネルギー量」を当然比較するわけで、差し引きするとキャンセルされますよね。

きっと、ルジャンドル変換には定数だけ任意性があるんだ・・・・・(‘;’)

まとめ

ルジャンドル変換を導きました(^^)/

\begin{align*}g=\sum_{i}(a_{i}b_{i})-f+(const)\cdot\cdot\cdot (9)\end{align*}

\begin{align*}\frac{\partial f}{\partial c_{i}}=-\frac{\partial g}{\partial c_{i}}\cdot\cdot\cdot (10)\end{align*}

とても覚えやすいですね。

(9)式
「別の関数」=「共通していない変数同士の積の和」ー「元の関数」

(10)式
「元の関数の\(c_{i}\)の偏微分」＝－「別の関数の\(c_{i}\)の偏微分」
※\(c_{i}\)は共通の変数