どうも(^^)/
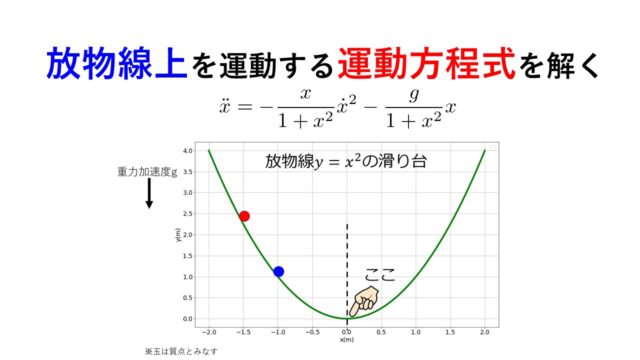
本日は、「ランダウ=リフシッツの”力学”」を読んでいて気になった一般速度\(\dot{q}_{i}\)を部分的に変換するラウシアンというのを紹介したいと思います。
「一般速度\(\dot{q}_{i}\)を部分的にってどういうこと?」ってなりますが、一般速度\(\dot{q}_{i}\)を全て一般運動量\(p_{i}\)にルジャンドル変換するとハミルトニアン\(H\)と言います。
「ランダウ=リフシッツの”力学”」の日本語版では”ラウス関数”という表記がありますが、ネットで調べてもラウス関数というのはあまり検索でヒットしないのですよね(笑)
もし、色々調べたければ「ラウシアン」と検索すると色々と検索に引っ掛かります(^^)/
では、ラウシアンを導いていきたいと思います。
本日は、「ラウシアン」の紹介だけで、導入までの手続きや何が嬉しいの?というのは追々アップします(^^)/
一般速度\(\dot{q}_{i}\)を部分的に変換する
解析力学の参考書などで最初に登場はラグランジアン\(L\)ですよね。
それは、系の<<力学的な状態>>を記述するのに互いに独立な変数である一般座標\(q_{i}\)と一般速度\(\dot{q}_{i}\)を用いて関数であるラグランジアン\(L(\{q_{i}\},\{\dot{q}_{i}\})\)導入し、
ラグランジュ方程式
に代入すれば運動方程式が導くことができるということで話しが進んでいきます。
しかし、系を記述するための変数は一般座標\(q_{i}\)と一般速度\(\dot{q}_{i}\)だけがすべてではないはずです。
一般速度\(\dot{q}_{i}\)を一般運動量\(p_{i}\)に変換して、系を記述する変数を一般座標\(q_{i}\)と一般運動量\(p_{i}\)としても良いわけです。
そのときに、ルジャンドル変換で一般速度\(\dot{q}_{i}\)を新しい変数である一般運動量\(p_{i}\)に変換して、関数ハミルトン\(H(\{q_{i}\},\{p_{i}\})\)を導入してのハミルトンの正準方程式を使って運動を予測する手続きをしたわけです。
このときは、全ての一般速度\(\dot{q}_{i}\)を新しい変数である一般運動量\(p_{i}\)に変換するので表にするとこんな感じです。
| ラグランジアン |
⇒ 全ての変数を変換!! ※(\(i=1~f\))\(f\)個の自由度 |
ハミルトニアン |
| \(L(\{q_{i}\},\{\dot{q}_{i}\})\) | \(H(\{q_{i}\},\{p_{i}\})\) | |
|
ラグランジュ方程式 \(\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_{i}}=\frac{\partial L}{\partial q_{i}}\) |
ハミルトニアンの正準方程式 \(\frac{dq_{i}}{dt}=\frac{\partial H}{\partial p_{i}}\) \(\frac{dp_{i}}{dt}=-\frac{\partial H}{\partial q_{i}}\)
|
※\(L(\{q_{i}\},\{\dot{q}_{i}\})\)は、\(L(q_{1},q_{2},\cdot\cdot\cdot,q_{n},\dot{q}_{1},\dot{q}_{2},\cdot\cdot\cdot\dot{q}_{n})\)を表しています。
書くのが面倒なので(笑)
部分的に変換するとは、
変数である一般速度\(\dot{q}_{1},\dot{q}_{2},・・・,\dot{q}_{i},・・・,\dot{q}_{m},\dot{\xi}_{1},\dot{\xi}_{2},・・・,\dot{\xi}_{j},・・・,\dot{\xi}_{n}\)とあったときに、\(\{\dot{q}_{i}\}\)については一般運動量\(\{p_{i}\}\)に変換しますが、
一般速度\(\{\dot{\xi}_{j}\}\)については一般速度\(\{\dot{\xi}_{j}\}\)のままにしておくということを意味しています。
このようにした方が便利な場合もあるのです。
| ラグランジアン |
|
ラウシアン |
| \(L(\{q_{i}\},\{\xi_{i}\},\{\dot{q}_{i}\}\{\dot{\xi}_{i}\})\) |
|
\(R(\{q_{i}\},\{\xi_{i}\},\{p_{i}\}\{\dot{\xi}_{i}\})\) |
|
ラグランジュ方程式 \(\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_{i}}=\frac{\partial L}{\partial q_{i}}\) \(\frac{d}{dt}\frac{\partial L}{\partial \dot{\xi}_{j}}=\frac{\partial L}{\partial \xi_{j}}\) |
⇒ 部分的に変数を変換!! ※(\(i=1~m\))\(m\)個の自由度 |
ハミルトニアンの正準方程式 \(\frac{dq_{i}}{dt}=\frac{\partial R}{\partial p_{i}}\)・・・② \(\frac{dp_{i}}{dt}=-\frac{\partial R}{\partial q_{i}}\)・・・③
|
|
⇒ 変数を変換しない!! ※(\(j=1~n\))\(n\)個の自由度 |
ラグランジュ方程式 \(\frac{d}{dt}\frac{\partial R}{\partial \dot{\xi}_{j}}=\frac{\partial R}{\partial \xi_{j}}\)・・・④
|
このときにラグランジア\(L(\{q_{i}\},\{\xi_{i}\},\{\dot{q}_{i}\}\{\dot{\xi}_{i}\})\)からラウシアンへ\(R(\{q_{i}\},\{\xi_{i}\},\{\dot{q}_{i}\}\{\dot{\xi}_{i}\})\)の変換は、
です。
変数を変換したいものだけ⑤のようにルジャンドル変換をすれば良いのですね。
まとめ
表を見て頂ければお分かりの通り、
\(\{q_{i}\}\)や\(\{p_{i}\}\)についてはハミルトンの正準方程式を使い、
\(\{\xi_{i}\}\)や\(\{\dot{\xi}_{i}\}\)についてはそのままラグランジュ方程式を使うということになります。
へ~っていう感じ(笑)
次回
ラウシアン\(R\)を導入するまでの手続きを見ていきましょう。
↓記事はこちらです。