正準変換で成り立つ関係式：マクスウェルの関係式

前回は、母関数のまとめと熱力学で出てくるマクスウェルの関係式について軽く触れました。

 

以下の熱力学的関数を変換する際にルジャンドル変換が使われます。

内部エネルギー：\(U(S, V, N)\)
エンタルピー ：\(H(S, p, N)\)
ヘルムホルツの自由エネルギー ：\(F(T, V, N)\)
ギブスの自由エネルギー：\(G(T, p, N)\)

※粒子数が一定の場合は\(N\)は定数

 

それで各変数は、

\(\big(\frac{\partial T}{\partial V}\big)_{S}=-\big(\frac{\partial P}{\partial S}\big)_{V}\)

\(\big(\frac{\partial T}{\partial P}\big)_{S}=\big(\frac{\partial V}{\partial S}\big)_{P}\)

\(\big(\frac{\partial S}{\partial P}\big)_{T}=-\big(\frac{\partial V}{\partial T}\big)_{P}\)

\(\big(\frac{\partial S}{\partial V}\big)_{T}=\big(\frac{\partial P}{\partial T}\big)_{V}\)

 

こんな感じで関係式があるのでした。

これがマクスウェルの関係式です。

 

熱力学か統計力学の教科書に出てくる重要な関係式ですね。

この関係式を使いながら問題を解きやすくしたり、測定困難な量を測定がしやすい変数に変えたりして議論を進めていくわけです。

 

本記事

解析力学でも、母関数を通してマクスウェルの関係式を導こう！！

 

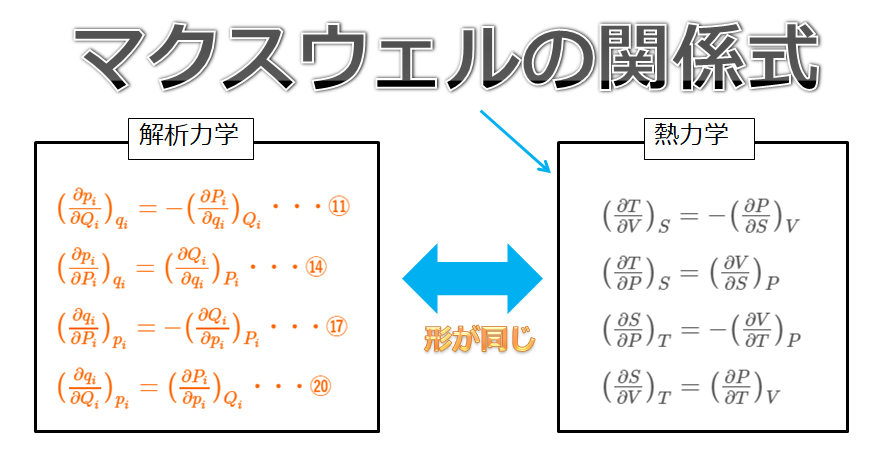
こういう対応付けがあるでしょうというのが本記事の言いたいことです。

 

まずは母関数のまとめから復習しましょう！！

 

母関数のまとめ

 

>>母関数：正準変換（第18.2報）

ざっくりと言ってしまえば、

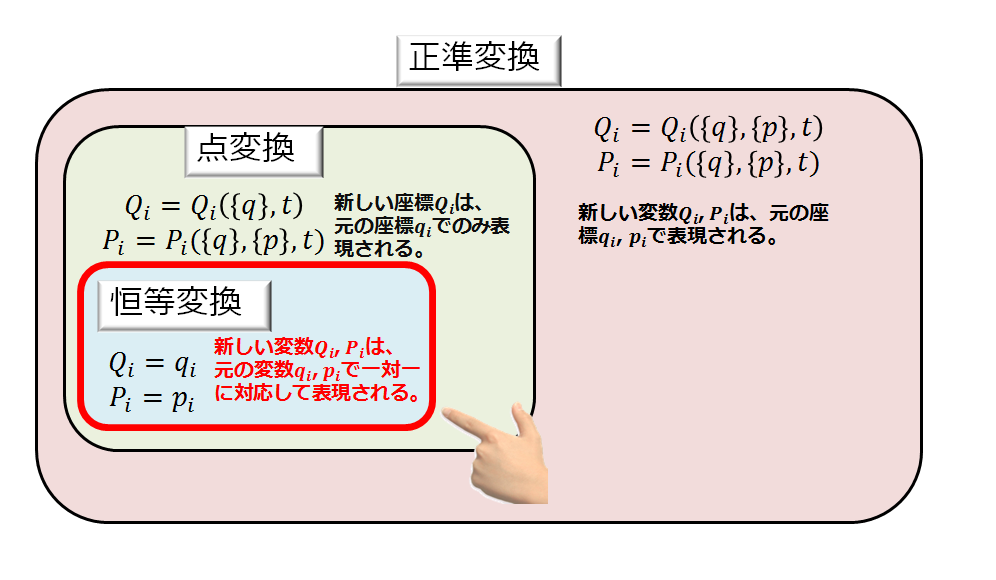
元の変数\(\{q_{i}\}\)と\(\{p_{i}\}\)から一組選び、新しい変数\(\{Q_{i}\}\)と\(\{P_{i}\}\)から一組選ぶ方法の合計4パターンの変数の選び方があるのです。

 

 

 

 

微分して関係式を導出

 

 

上の表から式を順に並べてみます。

\(p_{i}=\frac{\partial W_{1}}{\partial q_{i}}\)・・・①

\(P_{i}-\frac{\partial W_{1}}{\partial Q_{i}}\)・・・②

 

\(p_{i}=\frac{\partial W_{2}}{\partial q_{i}}\)・・・③

\(Q_{i}=\frac{\partial W_{2}}{\partial P_{i}}\)・・・④

 

\(q_{i}=-\frac{\partial W_{3}}{\partial p_{i}}\)・・・⑤

\(Q_{i}=\frac{\partial W_{3}}{\partial P_{i}}\)・・・⑥

 

\(q_{i}=-\frac{\partial W_{4}}{\partial p_{i}}\)・・・⑦

\(P_{i}=-\frac{\partial W_{4}}{\partial Q_{i}}\)・・・⑧

 

 

上から順番に並べただけです。

 

以下は、同じ手順をただ繰り返して関係式を出すだけです。

 

 

①②式を使って関係式を導出

 

\(q_{i}\)を固定して①を\(Q_{i}\)を偏微分

\(\big(\frac{\partial p_{i}}{\partial Q_{i}}\big)_{q_{i}}=\frac{\partial^2 W_{1}}{\partial Q_{i}\partial q_{i}}\)・・・⑨

 

\(Q_{i}\)を固定して②を\(q_{i}\)を偏微分

\(\big(\frac{\partial P_{i}}{\partial q_{i}}\big)_{Q_{i}}=-\frac{\partial^2 W_{1}}{\partial q_{i}\partial Q_{i}}\)・・・⑩

 

シュワルツの定理より、

\(\frac{\partial^2 W_{1}}{\partial Q_{i}\partial q_{i}}=\frac{\partial^2 W_{1}}{\partial q_{i}\partial Q_{i}}\)

なので、

 

\(\big(\frac{\partial p_{i}}{\partial Q_{i}}\big)_{q_{i}}=-\big(\frac{\partial P_{i}}{\partial q_{i}}\big)_{Q_{i}}\)・・・⑪

 

まずひとつ目の関係式を導くことができました。

 

 

③④式を使って関係式を導出

 

\(q_{i}\)を固定して③を\(P_{i}\)を偏微分

\(\big(\frac{\partial p_{i}}{\partial P_{i}}\big)_{q_{i}}=\frac{\partial^2 W_{2}}{\partial P_{i}\partial q_{i}}\)・・・⑫

 

\(P_{i}\)を固定して②を\(q_{i}\)を偏微分

\(\big(\frac{\partial Q_{i}}{\partial q_{i}}\big)_{P_{i}}=\frac{\partial^2 W_{2}}{\partial q_{i}\partial P_{i}}\)・・・⑬

 

シュワルツの定理より、

\(\frac{\partial^2 W_{2}}{\partial P_{i}\partial q_{i}}=\frac{\partial^2 W_{2}}{\partial q_{i}\partial P_{i}}\)

なので、

 

\(\big(\frac{\partial p_{i}}{\partial P_{i}}\big)_{q_{i}}=\big(\frac{\partial Q_{i}}{\partial q_{i}}\big)_{P_{i}}\)・・・⑭

 

二つ目の関係式が導けました！

 

⑤⑥式を使って関係式を導出

 

\(p_{i}\)を固定して⑤を\(P_{i}\)を偏微分

\(\big(\frac{\partial q_{i}}{\partial P_{i}}\big)_{p_{i}}=-\frac{\partial^2 W_{3}}{\partial P_{i}\partial p_{i}}\)・・・⑮

 

\(P_{i}\)を固定して⑥を\(p_{i}\)を偏微分

\(\big(\frac{\partial Q_{i}}{\partial p_{i}}\big)_{P_{i}}=\frac{\partial^2 W_{3}}{\partial p_{i}\partial P_{i}}\)・・・⑯

 

シュワルツの定理より、

\(\frac{\partial^2 W_{3}}{\partial P_{i}\partial p_{i}}=\frac{\partial^2 W_{3}}{\partial P_{i}\partial p_{i}}\)

なので、

 

\(\big(\frac{\partial q_{i}}{\partial P_{i}}\big)_{p_{i}}=-\big(\frac{\partial Q_{i}}{\partial p_{i}}\big)_{P_{i}}\)・・・⑰

 

3つ目が導けました。

 

あとひとつです。

 

 

⑦⑧式を使って関係式を導出

 

\(p_{i}\)を固定して⑦を\(Q_{i}\)を偏微分

\(\big(\frac{\partial q_{i}}{\partial Q_{i}}\big)_{p_{i}}=-\frac{\partial^2 W_{4}}{\partial Q_{i}\partial p_{i}}\)・・・⑱

 

\(Q_{i}\)を固定して⑧を\(p_{i}\)を偏微分

\(\big(\frac{\partial P_{i}}{\partial p_{i}}\big)_{Q_{i}}=-\frac{\partial^2 W_{4}}{\partial p_{i}\partial Q_{i}}\)・・・⑲

 

シュワルツの定理より、

\(\frac{\partial^2 W_{4}}{\partial Q_{i}\partial p_{i}}=\frac{\partial^2 W_{4}}{\partial p_{i}\partial Q_{i}}\)

なので、

 

\(\big(\frac{\partial q_{i}}{\partial Q_{i}}\big)_{p_{i}}=\big(\frac{\partial P_{i}}{\partial p_{i}}\big)_{Q_{i}}\)・・・⑳

 

 

まとめ

 

 

こうして無事に各変数の関係式を導くことができました(^^)

 

\(\big(\frac{\partial p_{i}}{\partial Q_{i}}\big)_{q_{i}}=-\big(\frac{\partial P_{i}}{\partial q_{i}}\big)_{Q_{i}}\)・・・⑪

\(\big(\frac{\partial p_{i}}{\partial P_{i}}\big)_{q_{i}}=\big(\frac{\partial Q_{i}}{\partial q_{i}}\big)_{P_{i}}\)・・・⑭

\(\big(\frac{\partial q_{i}}{\partial P_{i}}\big)_{p_{i}}=-\big(\frac{\partial Q_{i}}{\partial p_{i}}\big)_{P_{i}}\)・・・⑰

\(\big(\frac{\partial q_{i}}{\partial Q_{i}}\big)_{p_{i}}=\big(\frac{\partial P_{i}}{\partial p_{i}}\big)_{Q_{i}}\)・・・⑳

 

 

 

熱力学のマクスウェルの関係式と比較

 

 

母関数\(W_{1}\)に対して、変数は\(q_{i}\)と\(Q_{i}\)でした。

母関数\(W_{1}\)から母関数\(W_{2}\)へ変換するとき、

\(W_{1}(\{q_{i}\},\{Q_{i}\})\)

↓\(\{Q_{i}\}\)→\(\{P_{i}\}\)

\(W_{2}(\{q_{i}\},\{P_{i})\}\)

ルジャンドル変換で変数を\(q_{i}\)と\(P_{i}\)に変えました。

その時の、\(W_{1}\)と\(W_{2}\)の関係式はルジャンドル変換をすることで、

\(W_{2}(\{q_{i}\},\{P_{i}\})=W_{1}(\{q_{i}\},\{Q_{i}\})+\sum_{i}P_{i}Q_{i}\)

とこのようになります。

 

これを、

母関数\(W_{1}(q,Q)\)⇔内部エネルギー\(U(S,V)\)

↓\(V\)を\(P\)に変換

母関数\(W_{2}(q,P)\)⇔エンタルピー\(H(S,P)\)

と対応付ければ、

内部エネルギーからエンタルピー

\(U(S,V)=H(S,P)-PV\)
or
\(H(S,P)=U(S,V)+PV\)

のような関係式と同じであることがわかります。

 

詳細は示しませんが、母関数\(W_{3}\)、\(W_{4}\)を使うと熱力学でのヘルムホルツの自由エネルギーやギブスの自由エネルギーのような関係式が導けます。

それは当たり前なのかもしれませんが、熱力学の範囲では２つの独立変数を定めれば、熱力学的な状態は決まるわけでして、変数変換はルジャンドル変換を施すことで自由に変数を選べるわけです。

そう考えると、今考えている解析力学での問題（というか数学的な手続き）においては全く同じ考え方です。

 

各変数に対して、

\(q\)⇔\(S\)

\(Q\)⇔\(V\)

\(p\)⇔\(T\)

\(P\)⇔\(P\)

※同じ\(P\)でややこしいですが、右側の変数は圧力\(P\)です。

 

とすれば、

 

\(\big(\frac{\partial T}{\partial V}\big)_{S}=-\big(\frac{\partial P}{\partial S}\big)_{V}\)

\(\big(\frac{\partial T}{\partial P}\big)_{S}=\big(\frac{\partial V}{\partial S}\big)_{P}\)

\(\big(\frac{\partial S}{\partial P}\big)_{T}=-\big(\frac{\partial V}{\partial T}\big)_{P}\)

\(\big(\frac{\partial S}{\partial V}\big)_{T}=\big(\frac{\partial P}{\partial T}\big)_{V}\)

となり、マクスウェルの関係式となります。

\(V\)：体積
\(P\)：圧力
\(S\)：エントロピー
\(T\)：温度

 

 

物理的な意味での類似ももちろんあるのですが、ここでは数学的な手続きが全く同じなので、同じ形の関係式が導けたということだけでしょう・・・・・と思います。