こんにちは(@t_kun_kamakiri)(^^)/
そういえば前回、こんなこと書きました。
前回の記事はこちら
前回の復習を簡単にすると、
「ある関数U(x,y)がある拘束条件g(x,y)=0もとで最小となる場合を考えた時、どのような式が導かれるか？」
↓それって・・・（上の文面だけ見たら・・・）
運動方程式じゃない？？
もしくは力のつり合い？？
ってことは、「運動方程式」or「力のつり合い」に値するものではないか？？
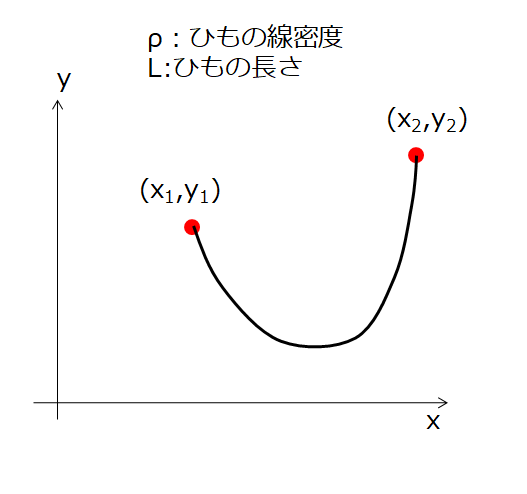
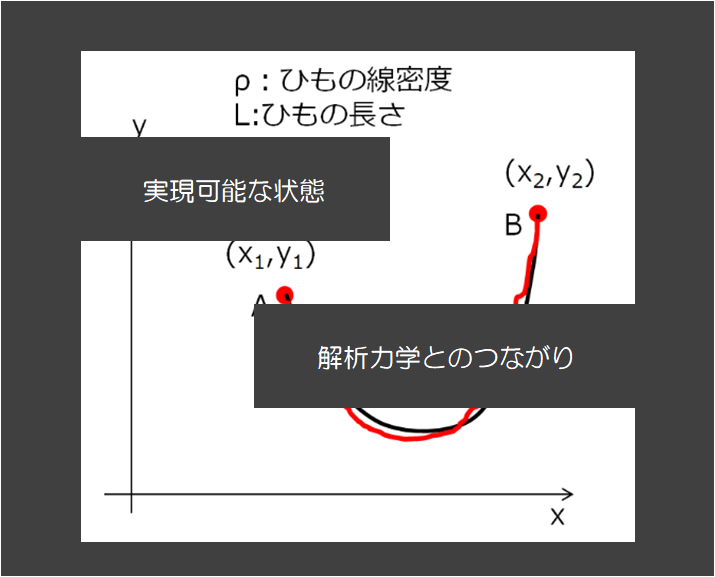
前回は、下記のような絵を持ってきて例題を持ちだしました。
ここで、
「ある関数\(U(x,y)\)がある拘束条件\(g(x,y)=0\)(ひもの長さが固定)もとで最小となる場合を考えた時、どのような式が導かれるか？」
・・・・（ゴリゴリ計算）
そうすると、下記の式が出てきました。
\begin{align*}\rho g\int_{A}^{B}\frac{y x^{\prime}\delta x^{\prime}}{\sqrt{1+x^{\prime}}}dy+\lambda \int_{A}^{B}\frac{x^{\prime}\delta x^{\prime}}{\sqrt{1+x^{\prime}}}dy=0\cdot\cdot\cdot (A)\end{align*}
そしたら、僕はこんなことを思ったのです・・・
この問題はラグランジュ方程式から考えて(A)を導いたのですが、力のつり合いから考えて(A)が導けるのではないかと考えました。そこで、本記事では力の釣り合いから(A)を導きたいと思います。
※実は計算があまりうまくいきませんでした。
最終的にはもう少しやさしい問題に変えて力の釣り合いから(A)のような形を導いています。
この記事を読むことで、ラグランジュ未定乗数法の\(\lambda\)の意味が少し見えてくると思います。
力のつり合いを考えよう
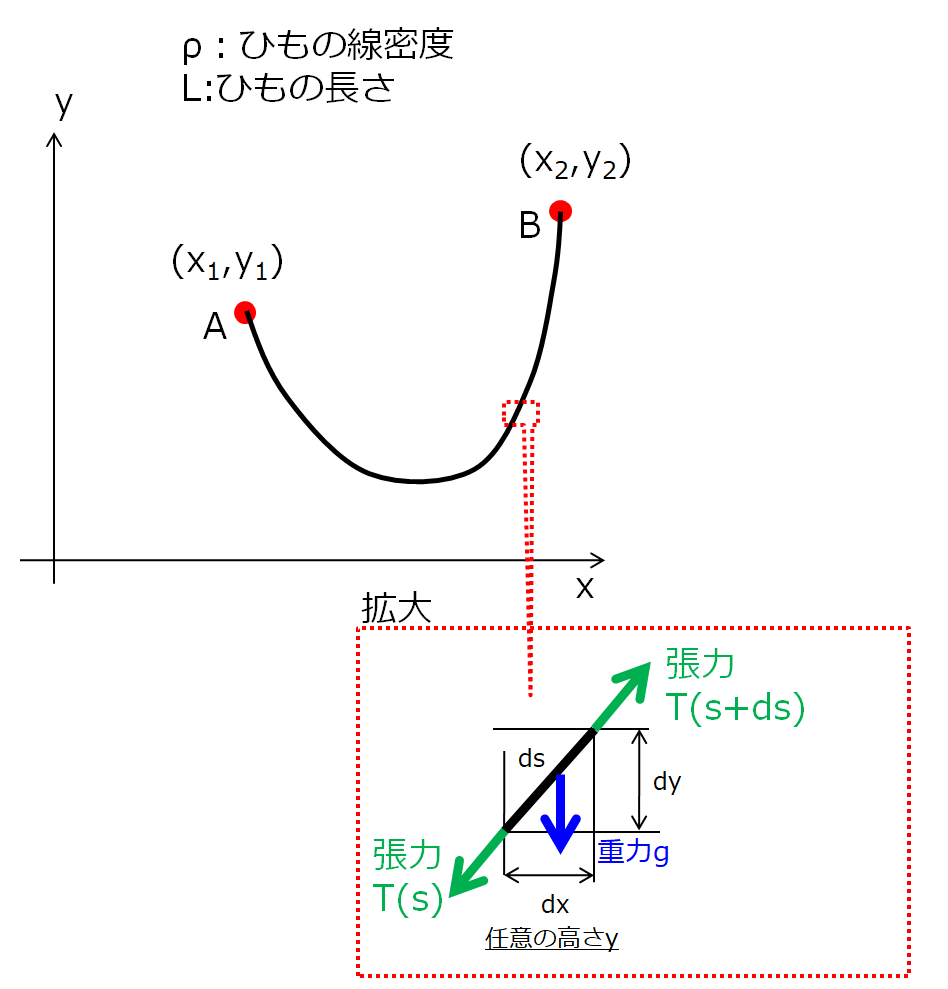
今考えている問題というのは下記のような状況ですね!(^^)!
絵のように微小区間としての力は、
- 重力：\(d\boldsymbol{F}=(0,\rho g d\boldsymbol{s})\)
- 張力：\(\boldsymbol{T}=(T_{x},T_{y})\)
この２つになりますね。
※ベクトル表記（太文字）にしてみました。
力のつり合いは、結局\(y\)方向だけ考えればよいのですが・・・・その前に・・・
張力がうっとおしいですね。
y方向の張力
\(T_{y}(s+ds)-T_{y}(s)\)がy方向の張力であるので、いつものように第1項をテーラー展開してdsの2次以降は無視してやります。
\begin{align*}T_{y}(s+ds)-T_{y}(s)=T_{y}(s)+\frac{T_{y}}{ds}ds-T_{y}(s)=\frac{dT_{y}}{ds}ds=\tau_{y}ds\cdot\cdot\cdot (1)\end{align*}
※見やすくするために、\(\tau_{y}=\frac{dT_{y}}{ds}\)とおきました。
単位長さ当たりの力ですね（SI単位系だとN/m）。確か表面張力もこんな単位だったような。。。
それじゃ～拡大した絵の微小領域で、力のつり合いの式を立てましょう(^^)/
y方向の力のつり合い
(1)と重力が釣り合っているとすると、
\begin{align*}\rho g ds-\tau_{y}ds=0\cdot\cdot\cdot (2)\end{align*}
はい、力のつり合いの式が出ました。微小区間ですが・・・
(2)式を区間AからBで積分すれば、全長でのひもの力のつり合いの式になりますね!(^^)!
(2)式を積分しましょう。
\begin{align*}\int_{A}^{B}\rho g ds-\int_{A}^{B}\tau_{y}ds=0\cdot\cdot\cdot (3)\end{align*}
そこで前回同様、
\begin{align*}ds=\sqrt{dx^2+dy^2}=dy\sqrt{1+\frac{dx}{dy}}=dy\sqrt{1+x^{\prime}}\end{align*}
とおくことで、(3)式は、
\begin{align*}\int_{A}^{B}\rho g\sqrt{1+x^{\prime}} dy-\int_{A}^{B}\tau_{y}\sqrt{1+x^{\prime}} dy=0\cdot\cdot\cdot (B)\end{align*}
このようになります。
やりました♪力のつり合いの式が出ました。。
前回出した式と比較してみましょう。。
今回：力のつり合いから出した式
\begin{align*}\int_{A}^{B}\rho g\sqrt{1+x^{\prime}} dy-\int_{A}^{B}\tau_{y}\sqrt{1+x^{\prime}} dy=0\cdot\cdot\cdot (B)\end{align*}
前回：下記の条件のもと出した式
ポテンシャルエネルギー\(U(x,y)\)が、拘束条件\(g(x,y)=0\)(ひもの長さが固定)もとで最小となる場合を考えて導出した式
\begin{align*}\rho g\int_{A}^{B}\frac{y x^{\prime}\delta x^{\prime}}{\sqrt{1+x^{\prime}}}dy+\lambda \int_{A}^{B}\frac{x^{\prime}\delta x^{\prime}}{\sqrt{1+x^{\prime}}}dy=0\cdot\cdot\cdot (A)\end{align*}
おー！！なんとも微妙に似ておりますな(笑)
(B)をの積分の中を\(x^{\prime}\)で微分できれば(A)になってくれそうな気配を感じます。。と、ここで僕は計算をやめちゃいました(笑)
何も複雑に計算をすることが目的ではなかったからです（言い訳・・・(*_*)）
次のような考察で十分でしょう。
(B)式は純粋に力のつり合いの式から求めました。
力を分解すると・・・
重力＋張力=0・・・(β)
(A)式は、ポテンシャルエネルギー（つまり重力に起因するエネルギー）と拘束条件（ひもの長さを固定）から未定数\(\lambda\)を導入して導きました。
だから次のように表現しても良いでしょう！
重力（に起因するポテンシャル項）＋拘束条件＝０・・・(α)
ここでなるほど、(β)と（α）を見比べたら、「張力⇔拘束条件」
すなわち、「拘束条件があるから張力が発生している」
と、このように結論付けることができました。
前回の僕の仮説に対する結論
「ある関数U(x,y)がある拘束条件g(x,y)=0もとで最小となる場合を考えた時、どのような式が導かれるか？」
↓それって・・・（上の文面だけ見たら・・・）
運動方程式じゃない？？
もしくは力のつり合い？？
ってことは、「運動方程式」or「力のつり合い」に値するものではないか？？
これに対しては、「力のつりあいの式に似たもの（(B)式）」が出ました(笑)
如何ともしがたいほど、ヌルッとした結論である。。
くやしい。。。どうして最後まで計算しなかったのか？
わからないからか？
どこか間違っているからか？
いや・・・・
最大の理由は、「積分とか微小区間とか、とにかく式がやかましい(笑)」
つまり、めんどくさすぎる！！
ってことで、シンプルにやっちゃいましょー(^^)/
シンプルな問題で「ラグランジュ未定乗数法＝力のつり合いの式」を導く
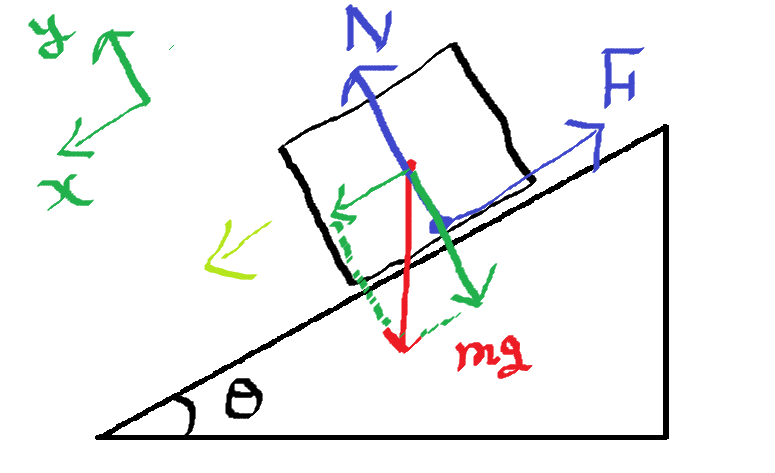
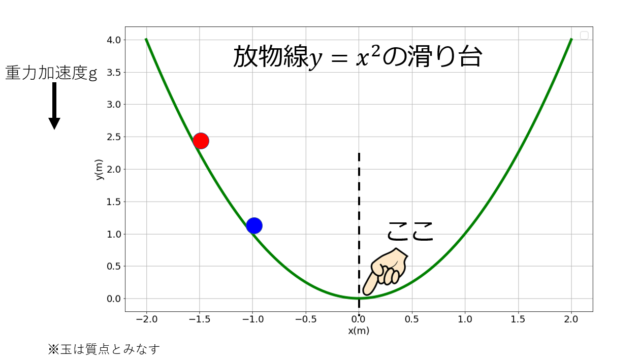
めちゃめちゃシンプルな「斜面に物体が乗っており、\(x=a\)の位置で滑らない(斜面上が\(y=0\)）」状況を考えたいと思います。
やりたいことは、「ラグランジュ未定乗数法を用いて力のつり合いの式になるか？」
これを見てみたいと思います。
まずは、物体にかかる力を考えます
\begin{align*}\boldsymbol{f}=(mg\sin\theta,-mg\cos\theta)\cdot\cdot\cdot (4)\end{align*}
x,y方向に力を分解すると、このようになりますね。
そして、重力はポテンシャルエネルギーなので、
\begin{align*}\boldsymbol{f}=-\boldsymbol{\nabla}U=\bigg(-\frac{\partial U}{\partial x},-\frac{\partial U}{\partial y}\bigg)\cdot\cdot\cdot (5)\end{align*}
(4)、(5)式をまとめると、
\begin{align*}\boldsymbol{f}=(mg\sin\theta,-mg\cos\theta)=\bigg(-\frac{\partial U}{\partial x},-\frac{\partial U}{\partial y}\bigg)\cdot\cdot\cdot (6)\end{align*}
となります。
次に、拘束条件を考えます
拘束条件は、斜面の上で止まっていますので、
\begin{align*}y=0\cdot\cdot\cdot (7)\end{align*}
となります。
そこで、毎度お馴染みの「ラグランジュ未定乗数法」を適用するために、(7)式を
\(g(x,y)=y\)とおけば、
拘束条件は、\(g(x,y)=0\cdot\cdot\cdot (8)\)
となります。
あ、もう一つ拘束条件がありました
もうひとつ拘束条件がありました(笑)
これだと滑り落ちますね・・・
\(x=a\)の位置で止まっています。
なので、\(h(x,y)=x-a\)とおき、
もうひとつ拘束条件、\(h(x,y)=0\cdot\cdot\cdot (9)\)
こちらを加えます。
ラグランジュ未定乗数法の適用
ラグランジュ未定乗数法は下記のような内容でしたね。
「ある関数\(U(x,y)\)がある拘束条件\(g(x,y)=0\)もとで最小となる場合を考えるた時、どのような式が導かれるか？」
↓それは
あらゆる仮想の変位\(\delta x\)、\(\delta y\)に対して
\begin{align*}\frac{\partial U}{\partial x}+\lambda\frac{\partial g}{\partial x}=0\end{align*}
\begin{align*}\frac{\partial U}{\partial y}+\lambda\frac{\partial g}{\partial y}=0\end{align*}
さっそく、(6)、(8)、(9)式を使って上の式にぶち込みましょう！！
あれ？今の場合は、拘束条件が2つ（(8)、(9)式）ありますね。
足しちゃえ(笑)
\begin{align*}\frac{\partial U}{\partial x}+\lambda_{1}\frac{\partial g}{\partial x}+\lambda_{2}\frac{\partial h}{\partial x}=0\end{align*}
\begin{align*}\frac{\partial U}{\partial y}+\lambda_{1}\frac{\partial g}{\partial y}+\lambda_{2}\frac{\partial h}{\partial y}=0\end{align*}
・・・
・・・
さて、やりましょう♪
\begin{align*}\frac{\partial U}{\partial x}+\lambda_{1}\frac{\partial g}{\partial x}+\lambda_{2}\frac{\partial h}{\partial x}=0\end{align*}
↓
\begin{align*}-mg\sin\theta+0+\lambda_{2}=0\cdot\cdot\cdot (10)\end{align*}
\begin{align*}\frac{\partial U}{\partial y}+\lambda_{1}\frac{\partial g}{\partial y}+\lambda_{2}\frac{\partial h}{\partial y}=0\end{align*}
↓
\begin{align*}mg\cos\theta+\lambda_{1}+0=0\cdot\cdot\cdot (11)\end{align*}
(10)×\(\lambda_{1}\)-(11)×\(\lambda_{2}\)とすると、
\begin{align*}\lambda_{1}mg\sin\theta+\lambda_{2}mg\cos\theta=0\end{align*}
おー！
\begin{align*}\mu=-\frac{\lambda_{2}}{\lambda_{1}}\end{align*}
とおけば、
\begin{align*}mg\sin\theta=\mu mg\cos\theta\cdot\cdot\cdot (12)\end{align*}
力のつり合いの式になりました。
※\(\lambda_{1}\)、\(\lambda_{2}\)は特に正負はこだわらなくてもよかったのでしたよね。
\(\mu\)が俗に言う静止摩擦係数ですね。
整理すると・・・
\begin{align*}-mg\sin\theta+0+\lambda_{2}=0\cdot\cdot\cdot (10)\end{align*}
\(\lambda_{2}\)は何に起因しているのですか？
それは、「\(x=a\)の拘束条件」です。
「\(x=a\)で拘束されているのはなぜですか？」
それは、「摩擦力があるから」です。
\begin{align*}mg\cos\theta+\lambda_{1}+0=0\cdot\cdot\cdot (11)\end{align*}
\(\lambda_{1}\)は何に起因しているのですか？
それは、「y=0の拘束条件」です。
「\(y=0\)で拘束されているのはなぜですか？」
それは、「垂直抗力が働いているから」です。
このようになります。
ところで、
\begin{align*}mg\sin\theta=\mu mg\cos\theta\cdot\cdot\cdot (12)\end{align*}
を導くのに、「摩擦力」も「垂直抗力」も一言も使わずに導きましたよね。
とても不思議です。
出発点は、あくまで
「ある関数\(U(x,y)\)がある拘束条件\(g(x,y)=0\)もとで最小となる場合を考えるた時、どのような式が導かれるか？」
だけです。
その手法が、ラグランジュ未定乗数法というのですが、実は・・・
ある関数\(U(x,y)\)がある拘束条件\(g(x,y)=0\)もとで最小になるように状態が実現している・・・
と、このように解釈できます・・・と勝手に解釈しています。（もしくはそうなるように人が数式を構築している・・・）
次回
いったい、ランダウ＝リフシッツの”力学”のお話はどこにいったのやら・・・(笑)
だが、まだ脱線は続くのです♪
次回は、
ハミルトンの原理についてまとめましょうかね!(^^)!
次回の記事はこちら
参考図書
いくつかおすすめの解析力学の参考書を挙げておきます。
ランダウ力学
下記のような小教程もあります。
解析力学：マセマキャンパスゼミ
↑こちらは「スバラシク実力がつくと評判」シリーズの解析力学の参考書です。
著者は高校数学を教える予備校の講師で、とてもわかりやすいと評判です。
その方が書いた書籍なので高校生でも読みこなすことができるくらいわかりやすく、かつちゃんと大学の物理の内容を扱っています。
解析力学ⅠⅡ：朝倉物理学大系
この2冊は解析力学の名著ですね。
数学的な解説も多く、解析力学を深く学ぶ人には挑戦するには申し分ない内容です。
詳解 力学演習
こちらは「力学」と「解析力学」の演習問題を扱っている演習問題集になります。
![](<iframe style="border: none;" src="https://rcm-fe.amazon-adsystem.com/e/cm?o=9&p=13&l=ur1&category=audible&banner=07J5KH0DSN7BCRWR0F82&f=ifr&linkID=d1dd57270470731eb3c6d0054e4dffe8&t=korokoro00d-22&tracking_id=korokoro00d-22" width="468" height="60" frameborder="0" marginwidth="0" scrolling="no"></iframe>)
