こんにちは(@t_kun_kamakiri)(^^)/(これを書き始めたのが夜11時です)
前回の記事も載せておきます。
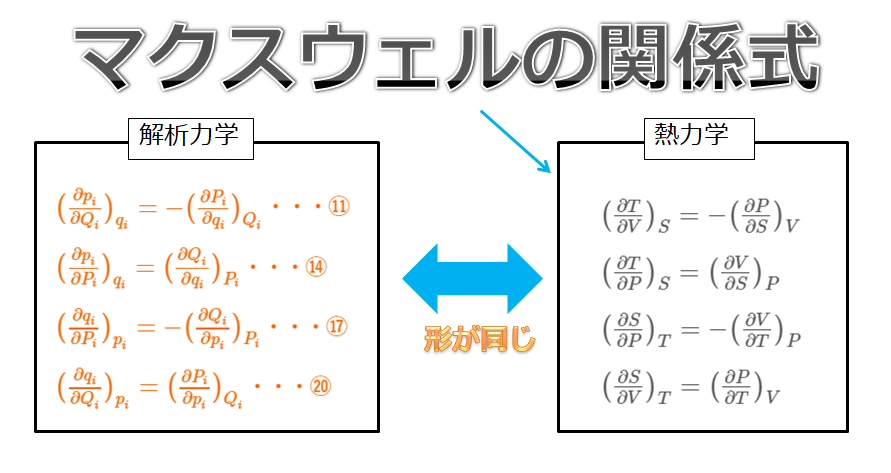
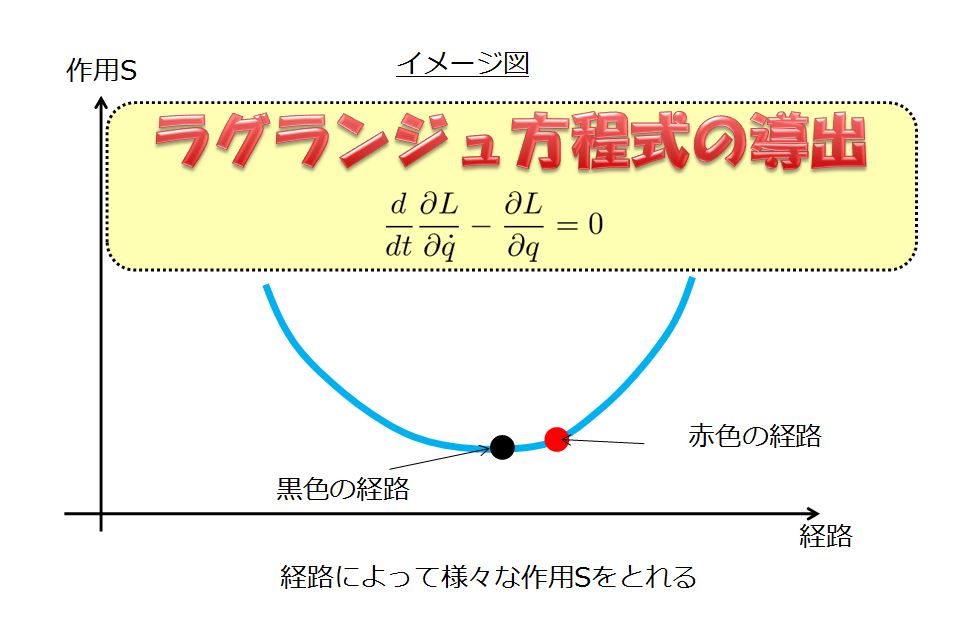
下記のように「最小作用の原理」からラグランジュ方程式を導出しました。
※ラグランジアン\(L\)
最小作用の原理はいったい誰が決めたのだ?って思ったことが本記事のきっかけです。
そこで、
もっと数学の場面で「最小作用の原理」や「ラグランジュ方程式」に近い考え方はないかと考えまして、
「ある関数\(U(x,y)\)が、ある拘束条件\(g(x,y)=0\)もとで最小となる場合を考えた時、どのような式が導かれるか?」
を考えれば一体どうなるの?
というとても抽象的なことを考え始めました。
ちなみに、上記の内容は数学では「ラグランジュ未定乗数法」というそうです。
問題設定
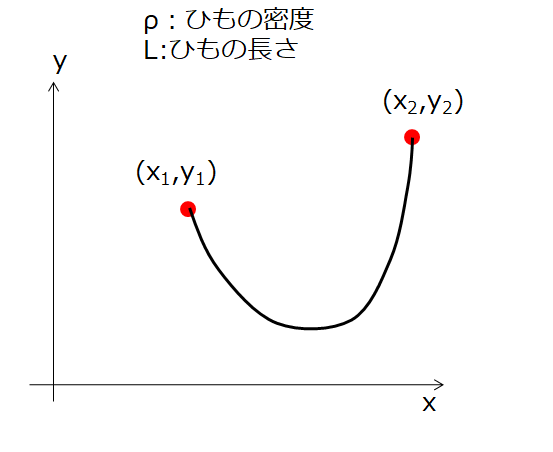
下記のように両端で固定された密度\(\rho\)、長さ\(L\)のひもがあったとします。
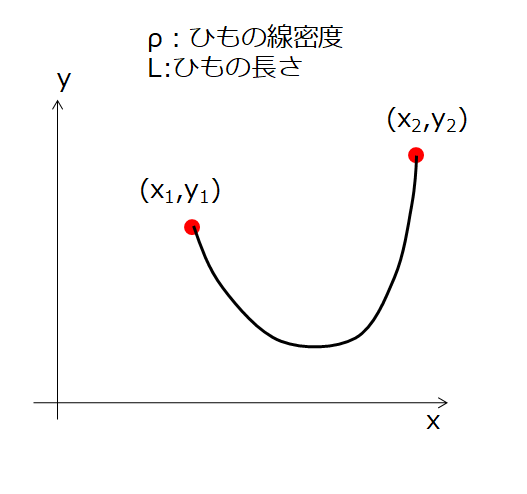
このとき、重力があるのでこのひもにはポテンシャルエネルギーがあります。
(位置エネルギーです)
微小長さ\(ds=\sqrt{x^2+y^2}\)なので、微小長さの質量\(\rho ds\)となります。
なので、ポテンシャルエネルギーは1から2まで積分してやればよいので、\(U=\int_{1}^{2}\rho g\,y\,ds\)と、ひとまずこのように書けますね。
ここで、
この系でつり合いが取れている状態(平衡状態)を考えるならば、
「状態として実現しているのはポテンシャルエネルギーが最小のとき」であるはずだ(感覚的に)。
ただし、この場合は両端で固定されて拘束条件\(L=\int_{1}^{2}ds\)が存在している。
ラグランジュ未定乗数法の上述したものと同じ考え方だ!!
と、なります。
ここでさらに、ポテンシャルエネルギーが最小になる状態が実現するって誰が決めたのだっていうことになりますが、それについては次回以降の「仮想仕事の原理」「ダランベールの原理」なども記事も書きますのでご了承ください。
目標設定
目標達成にはまずラグランジュ未定乗数法から学ばなければなりません。
ではいきましょう!!
ラグランジュ未定乗数法
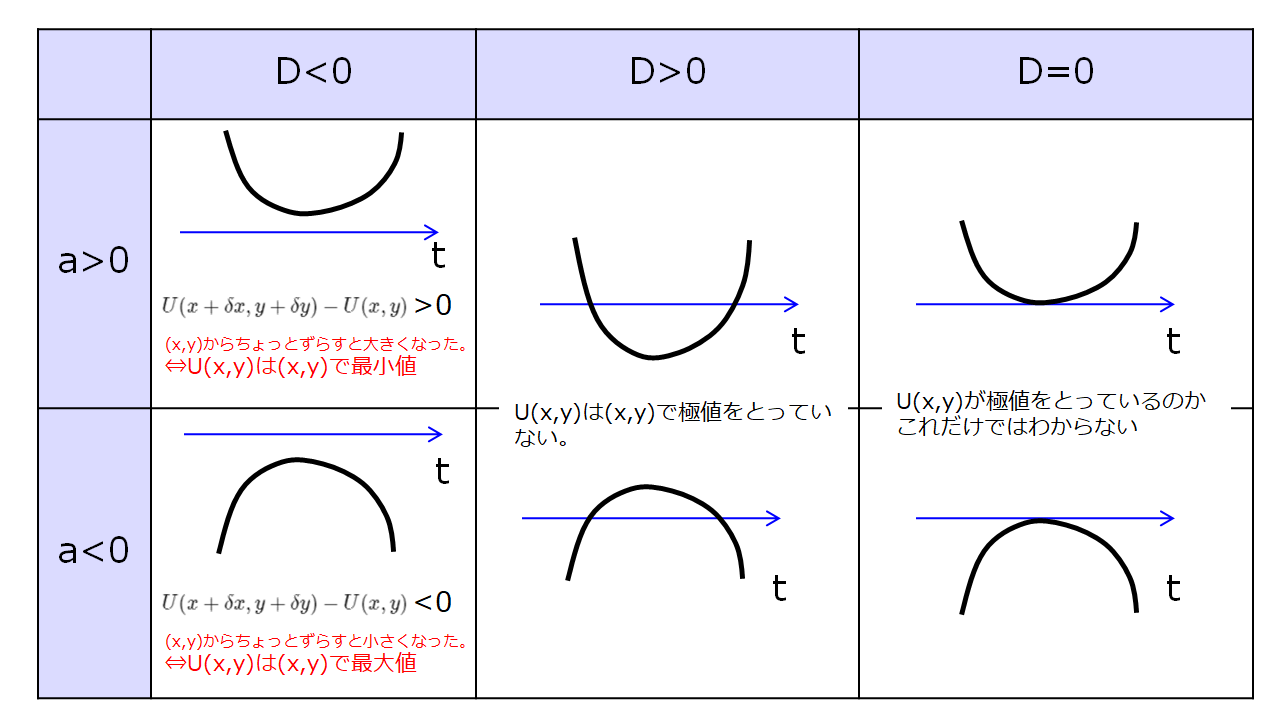
さきほどから出ている、「ある拘束条件のもと」、「ポテンシャルエネルギーを最小」にしているという状態は下記のような絵でイメージできます。
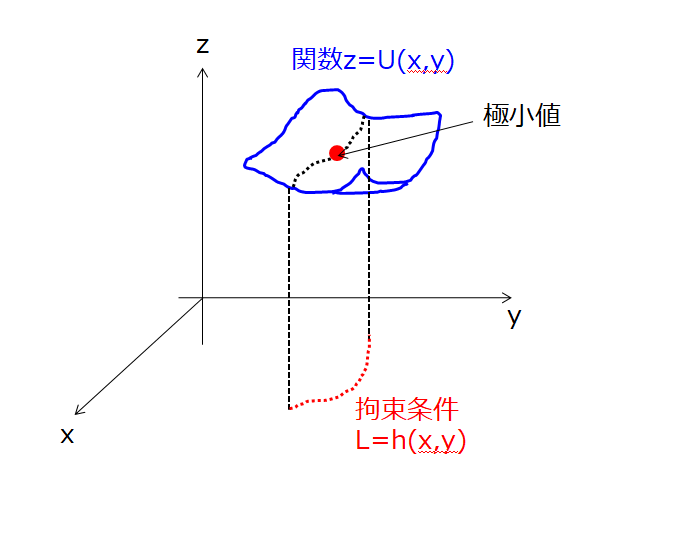
ポテンシャルエネルギー最小
ポテンシャルエネルギー最小の条件は簡単です。
ポテンシャルエネルギー最小となる必要条件(極値をとる条件)を求めればよいですね。
仮想の変位\(\delta x\)、\(\delta y\)に対して変化は無し、つまり
テーラ展開して\(\delta x\)、\(\delta y\)の2次の項を無視すると、
であることに着目すれば、
となります。
これが、\(U(x,y)\)が極値をとる条件です。
どんな仮想変位\(\delta x\)、\(\delta y\)で(1)式が成立と考えると、
\(\frac{\partial U}{\partial x}=0\) かつ \(\frac{\partial U}{\partial y}=0\)
と初めから考えても良かったのです。
ですが、後で(1)式の形として扱った方が便利なので、とりあえず(1)のままにしておきます。
でも、これだと特に条件がないのであらゆる\(x\)と\(y\)での最小値(もしくは最大値)をとってしまいますよね。
(極値は\((x,y)=(0,0)\)。式を見ても何となくそうなりそうですね。)
次に、拘束条件について考えましょう。
拘束条件について
拘束条件については、\(g(x,y)=h(x,y)-L\)とおけば、
が条件であることになります。
拘束条件なので、仮想の変位\(\delta x\)、\(\delta y\)としても条件が変わるわけではないですね。
さらに、テーラ展開して\(\delta x\)、\(\delta y\)の2次の項を無視すると、
g(x+\delta x, y+\delta y)=g(x,y)+\frac{\partial g}{\partial x}\delta x+\frac{\partial g}{\partial y}\delta y\cdot\cdot\cdot (4)\end{align*}
となります。
(2),(3),(4)式を眺めると、
が出てきました!(^^)!
ただ・・・こんなバラバラな式だと扱いずらいな(笑)
あらゆる仮想の変位\(\delta x\)、\(\delta y\)に対して(1)かつ(5)が成り立つならば、以下のようにしてまとめてしまいましょう。
(1)と(5)はまとめて、
\begin{pmatrix}
\frac{\partial U}{\partial x} & \frac{\partial U}{\partial y}\\
\frac{\partial r}{\partial x} & \frac{\partial g}{\partial y}
\end{pmatrix}
\begin{pmatrix}
\delta x\\
\delta y
\end{pmatrix}=0
\end{align*}
と、このように行列で書けます。
ここで、
\frac{\partial U}{\partial x} & \frac{\partial U}{\partial y} \\
\frac{\partial g}{\partial x} & \frac{\partial g}{\partial x}
\end{pmatrix}\end{align*}
と行列Aと置いて、あらゆる仮想の変位\(\delta x\)、\(\delta y\)に対して(6)式が成り立つのであれば、「Aの逆行列は存在しない」⇔「Aの行列式は0」である。
\frac{\partial U}{\partial x} & \frac{\partial U}{\partial y} \\
\frac{\partial g}{\partial x} & \frac{\partial g}{\partial y}
\end{vmatrix}=0\end{align*}
上記の行列式は、
となりますね。
さらに、
こうとも書けます。
これを見ると、関数が変わっても全く同じ形をしているので、両辺は特に\(x\)、\(y\)には依存していないことがわかります。
両辺を\(\lambda\)と置きましょう。
と、このようになります。
そうすると、下記のようにすっきりしました(^^)
※\(\lambda\)は定数なので、見やすくするために適当に正負を変えたり好きにしてください。
お分かりだと思いますが、(5)式と(6)式を結びつけるのに未知の定数λをあえて導入したので、未定ということで”未定乗数法”です。
僕が思ったこと(仮説)
わかったこと・・・
と、このようになりました。
次回
次回はひもの拘束の例題で「ラグランジュ未定乗数法(7)式、(8)式」を使って「どのような状態が実現するか?」を示したいと思います。
↓これ。
と、その前に・・・
「ラグランジュ未定乗数法」を使ったシンプルな数学の問題をやった方が良い気がしたので、次回は数学の問題です。
問題:
「\(x^2+2xy+y^2=1\)の条件のもとで、\(U=x^2+3y^2\)が極値をもつ点\((x,y)\)を求めよ」
↑これにしましょう(^^)/
参考図書
いくつかおすすめの解析力学の参考書を挙げておきます。
ランダウ力学
下記のような小教程もあります。
解析力学:マセマキャンパスゼミ
↑こちらは「スバラシク実力がつくと評判」シリーズの解析力学の参考書です。
著者は高校数学を教える予備校の講師で、とてもわかりやすいと評判です。
その方が書いた書籍なので高校生でも読みこなすことができるくらいわかりやすく、かつちゃんと大学の物理の内容を扱っています。
解析力学ⅠⅡ:朝倉物理学大系
この2冊は解析力学の名著ですね。
数学的な解説も多く、解析力学を深く学ぶ人には挑戦するには申し分ない内容です。
詳解 力学演習
こちらは「力学」と「解析力学」の演習問題を扱っている演習問題集になります。