【ラグランジュ方程式の導出】最小作用の原理からわかりやすく解説

さてやっていきましょう。前回の続きです。

前回は下記の内容で記事を書きました。

前回の記事はこちら

ランダウの力学の参考書はこちらですね↓

力学 (増訂第3版) ランダウ=リフシッツ理論物理学教程

エリ・ランダウ, イェ・エム・リフシッツ

2,200円(11/21 22:15時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

前回の復習からいきます。

前回の復習

「ある時刻における力学的状態は、一般化座標\(q_{i}\)と一般化速度\(\dot{q}_{i}\)というものを同時に与えれば、それ以降の運動は原理的に予言できる。」

ということを述べました。

一般化座標\(q_{i}\)と一般化速度\(\dot{q}_{i}\)というとても抽象的ものをなぜ導入したかというと、座標系によらない定式化を試みたかったからでしたね。

今回は、いよいよラグランジュ方程式を導きましょう(^^)/

本記事の内容

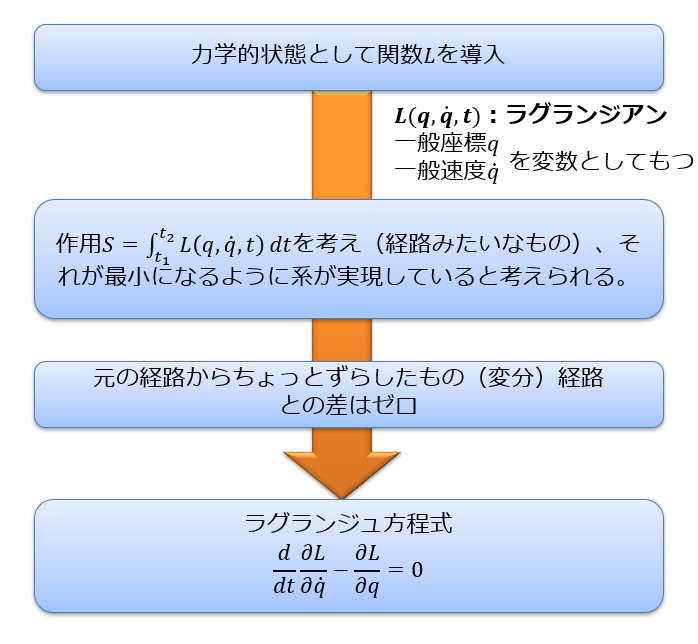
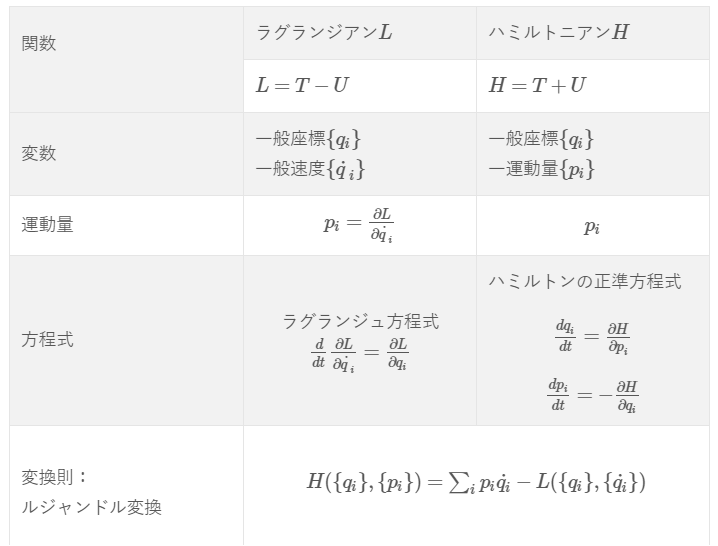
ラグランジュ方程式の導出

\begin{align*}\frac{d}{dt}\frac{\partial L}{\partial \dot{q}}-\frac{\partial L}{\partial q}=0\end{align*}

※ラグランジアン\(L\)

ランダウ・リフシッツの力学ではいきなり、\(L\)（ラグランジアンと言います）がでてきて序盤からつまづきます。

教科書のP.2でいきなりラグランジアンを導入しますからね(笑)

順を追って理解していきましょう。

最小作用の原理：状態は最短で次の状態へいく
まとめ
次回
参考図書

最小作用の原理：状態は最短で次の状態へいく

まずは、ラグランジュ方程式と深く関係している最小作用の原理について簡単に説明をしておきます。

最小作用の原理とは

最小作用の原理に従って、物体の運動（時間発展）は、作用積分と呼ばれる量を最小にするような軌道に沿って実現される。

子の解説だけでわかる人がいるのかと思うくらい、まーわけがわからない(笑)

とりあえず、前の記事で書きましたように、

ある時刻における力学的状態は、一般化座標\(q_{i}\)と一般化速度\(\dot{q}_{i}\)で決まる。

力学的な状態は、それらを変数とおく関数\(L\)というもので特徴づけられる・・・とします。

\(L\)はまだよくわからなくても良いですが、力学的な状態を示す関数という漠然としたイメージをもっておけば良いでしょう。

それが、時間\(t\)、一般座標\(q_{i}\)、一般速度\(\dot{q}_{i}\)を変数として、以下のように表記します。

\begin{align*}L(q_{i},\dot{q}_{i},t)\end{align*}

これをラグランジアンと言います。

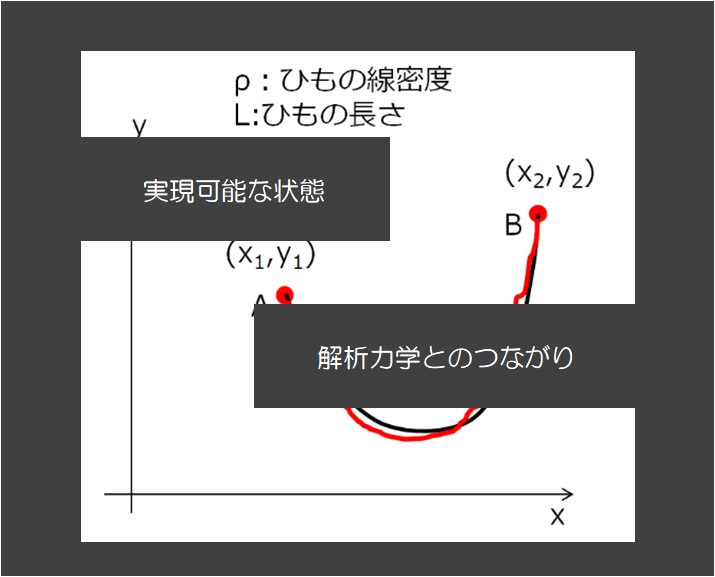
ここで、ラグランジュ方程式を導入する前に、ある状態1からある状態2にいく経路というものをイメージします。

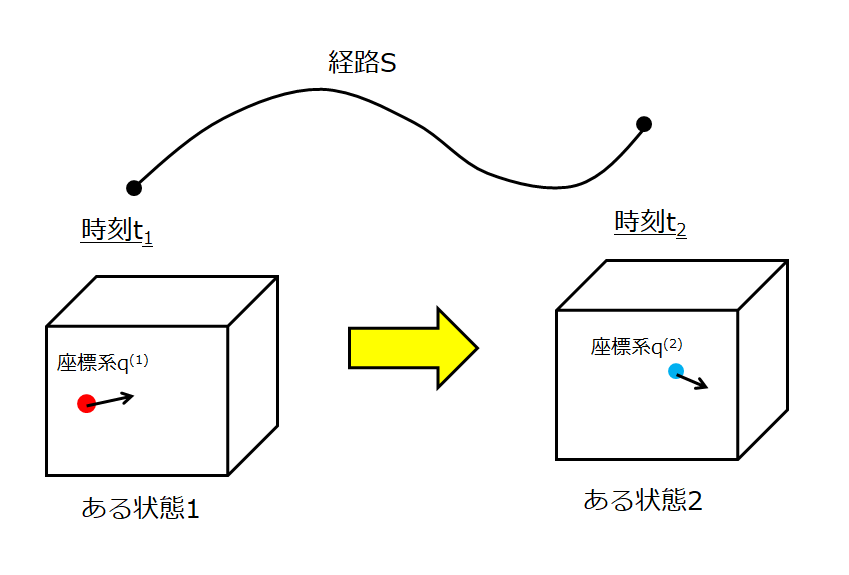
そうすると、状態経路みたいなものは、

\begin{align*}S=\int_{t_{1}}^{t_{2}}L(q_{i},\dot{q}_{i},t)dt\end{align*}

となりますね。これを作用といいます。

たんに、任意の時刻\(t_{1}\)と\(t_{2}\)での位置座標をそれぞれ\(q^{(1)}\)、\(q^{(2)}\)と示してあるにすぎません。

そして、力学的な状態は作用\(S\)を最小にするように実現している、これを最小作用の原理と言います。

何か例があると嬉しいですね。。。

ん～、今は思いつかないので記事を書きながら随時アップしていきます(´・ω・`)

「\(S\)は最小にとるように系が決められている」ということが前提にあるのであれば、\(q(t)\)をちょっとずらしたらどうなるのか？

\begin{align*}q(t)+\delta q(t)\end{align*}

と、このようにしてみます。

\(\delta q(t)\)のようなわずかなずれのことを変分と言います。

※ここで、時刻\(t_{1}\)から\(t_{2}\)の間、\(\delta q(t)\)はずっと小さな関数としています。
※また、条件として時刻\(t_{1}\)での\(q^{(1)}\)の変分\(\delta q^{(1)}\)は0、
時刻\(t_{2}\)での\(q^{(2)}\)の変分\(\delta q^{(2)}\)は0としてます。

これらの意味は、「初期状態の一般化座標\(q^{(1)}\)と最終状態の一般化座標\(q^{(2)}\)は変えずにその間の経路はわずかにかえるという操作を行います」という意味です。

スタート地点とゴール地点が同じというイメージですね。絵で示すと、下記の赤色の経路みたいな感じでしょうか。

このように経路を変えると様々な作用Ｓの値をとれるのです。

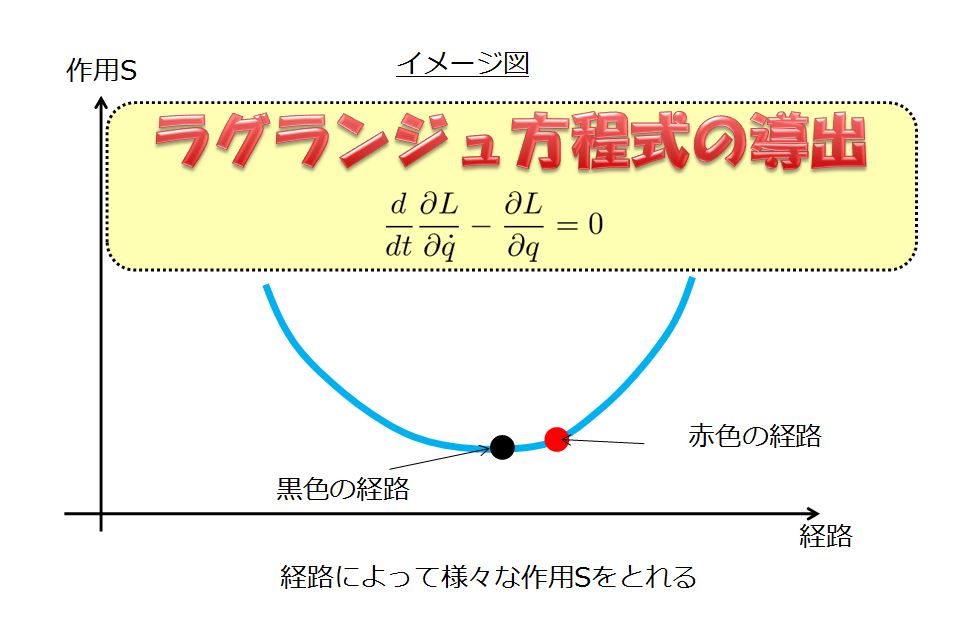
ここで、上の絵の黒色の経路による作用Sが最小であるということは、極値をとっていますよね。

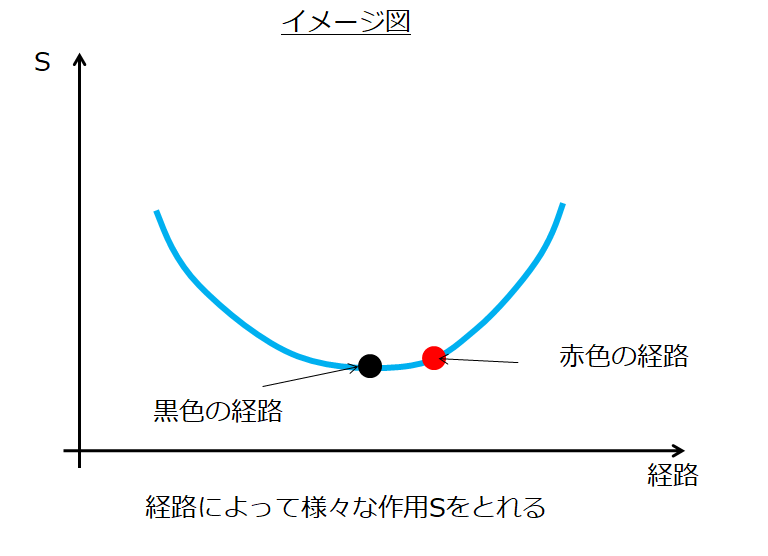
極値をとっているということは、作用\(S\)の微分が0とも言えるし、ここでは

①黒色経路：\( S=\int_{t_{1}}^{t_{2}}L(q_{i},\dot{q}_{i},t)dt\)

②赤色経路：\( S=\int_{t_{1}}^{t_{2}}L(q_{i}+\delta{q_{i}},\dot{q}_{i}+\delta{\dot{q}_{i}},t)dt\)

と考えた時の、①と②の差が0であると言えますね。

さて、計算します・・・・の前に(2)をちょっと式変形

(2)式の、

\begin{align*}L(q_{i}+\delta{q_{i}},\dot{q}_{i}+\delta{\dot{q}_{i}},t)d\end{align*}

をテーラー展開します。

\begin{align*}L(q_{i}+\delta{q_{i}},\dot{q}_{i}+\delta{\dot{q}_{i}},t)dt=L(q_{i},\dot{q}_{i},t)+\frac{\partial L}{\partial q_{i}}\delta q_{i}+\frac{\partial L}{\partial \dot{q}_{i}}\delta \dot{q}_{i}\end{align*}

ここで、\(\delta q\)などの2次の項は小さいの無視。

上式は次のようにも書けますね。

\begin{align*}\delta L=L(q_{i}+\delta{q_{i}},\dot{q}_{i}+\delta{\dot{q}_{i}},t)dt-L(q_{i},\dot{q}_{i},t)=\frac{\partial L}{\partial q_{i}}\delta q_{i}+\frac{\partial L}{\partial \dot{q}_{i}}\delta \dot{q}_{i}\end{align*}

さて、(2)ー(1)=0とします。

\begin{align*}\int_{t_{1}}^{t_{2}}L(q_{i}+\delta{q_{i}},\dot{q}_{i}+\delta{\dot{q}_{i}},t)dt-\int_{t_{1}}^{t_{2}}L(q_{i},\dot{q}_{i},t)dt=0\end{align*}

すると、

\begin{align*}\int_{t_{1}}^{t_{2}}\big(\frac{\partial L}{\partial q_{i}}\delta q_{i}+\frac{\partial L}{\partial \dot{q}_{i}}\delta \dot{q}_{i}\big)dt=0\end{align*}

このようになりました。

もうひといきです(^^)

第二項を部分積分してやりましょう。

\begin{align*}\int_{t_{1}}^{t_{2}} \frac{\partial L}{\partial q_{i}}\delta q_{i}dt+\bigg[\frac{\partial L}{\partial \dot{q}_{i}}\delta q_{i}\bigg]_{t_{1}}^{t_{2}}-\int_{t_{1}}^{t_{2}}\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_{i}} \delta q_{i}dt=0\end{align*}

式の順番を入れ替えて、

\begin{align*}\bigg[\frac{\partial L}{\partial \dot{q}_{i}}\delta q_{i}\bigg]_{t_{1}}^{t_{2}}+\int_{t_{1}}^{t_{2}}\big( \frac{\partial L}{\partial q_{i}}-\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_{i}}\big)\delta q_{i}dt=0\end{align*}

ここで、\(\delta q_{i}\)というのは、スタート地点と、ゴール地点で0でしたから、上の式の第一項は消えてしまいます。

見えてきました!(^^)!

\(\delta q\)は任意に与えましたから、任意の\(\delta q_{i}\)に対して上の式が恒等的に0になるためには、第二項の（）内が常にゼロでなければなりません。

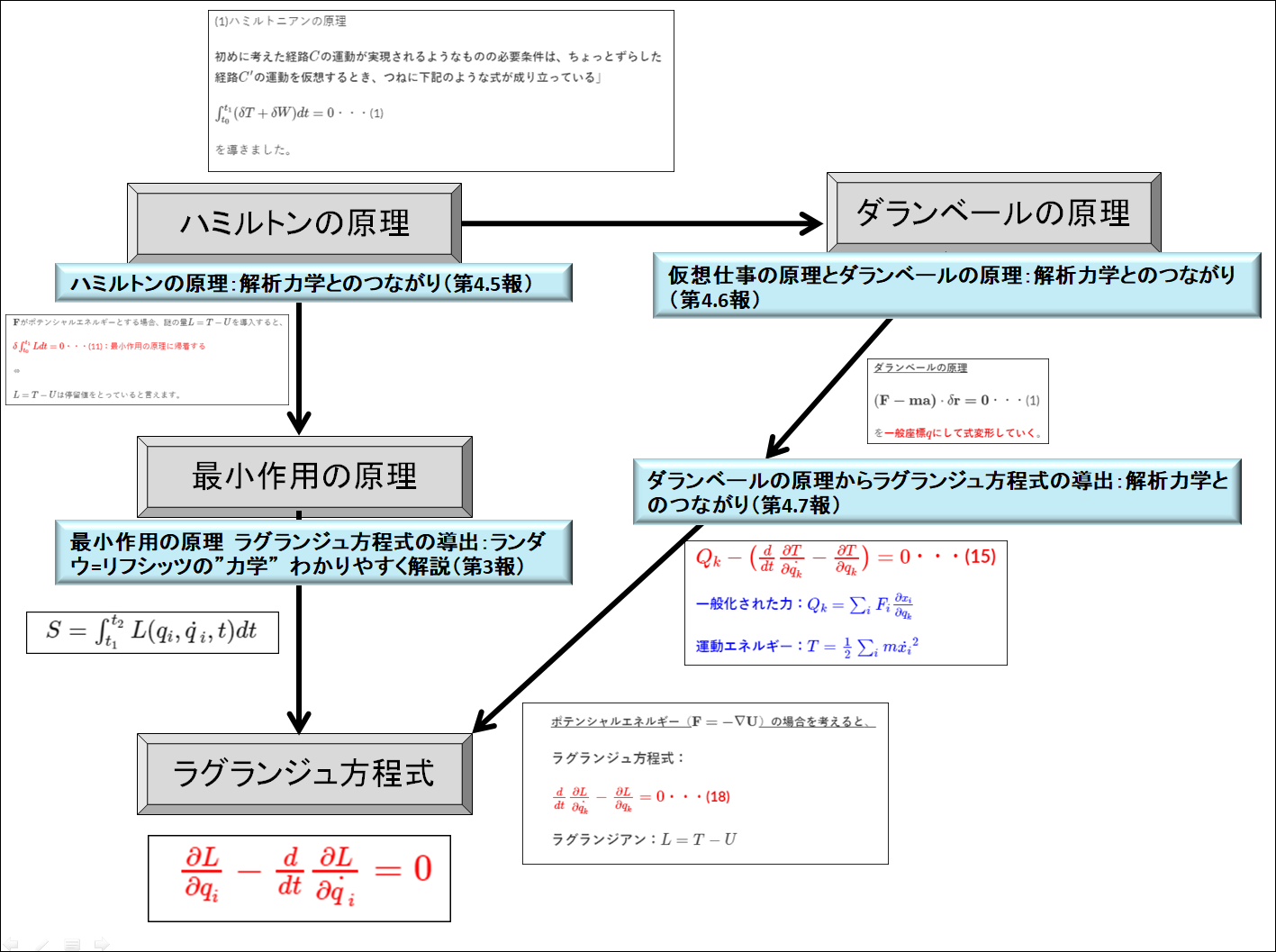
\begin{align*}\frac{\partial L}{\partial q_{i}}-\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_{i}}=0\end{align*}

これがラグランジュ方程式と呼ばれている方程式です。

まとめ

はじめて解析力学でラグランジュ方程式を導出した方は、なんだかよくわからないまま、ラグランジュ方程式

\begin{align*}\frac{\partial L}{\partial q_{i}}-\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_{i}}=0\end{align*}

が導けました感覚になるでしょう・・・・

今までの流れを今一度確認しておきましょう。

全体のフロー

次回

なんだか急にわけわからん方程式を立てたなという感じですね(笑)

次回の記事はこちら

ラグランジュ未定乗数法：解析力学とのつながり

ちなみに・・・

先の話を少し触れておくと・・・・

実は、与えられた系におけるラグランジアン\(L\)さえわかっていれば、ラグランジュ方程式を使えば、加速度を速度および座標の間の関係を示す式になるのです。

それは何かといえば、運動方程式です。

種明かしをすると、ラグランジアン\(L=T-U\)と置けば、ラグランジュ方程式に代入すれば、そのまま運動方程式になってしまいます。

※Tは運動エネルギー：\(T=\frac{1}{2}mv^{2}\)

※Uはポテンシャルエネルギー：\(U=mgh\)（高さhの位置にある質点）

不思議だ(笑)

たとえ座標系がデカルト座標系\((x,y,z)\)であろうと、極座標系\((r,\phi,\theta)\)であろうと、ラグランジアン\(L=T-U\)と置けば、ラグランジュ方程式から運動方程式が求まる。
デカルト座標系の\(x\)方向、\(y\)方向に関係なく、ラグランジアン\(L=T-U\)と置けば、ラグランジュ方程式からその方向の運動方程式が求まる。

こうして、一般的な形式化に成功しました。

一般座標\(q_{i}\)と一般速度\(\dot{q}_{i}\)をその座標系における変数に置き換えてラグランジュ方程式を取り扱えば良いということです。

素晴らしい(^^)

ラグランジアン\(L=T-U\)と置けば、ラグランジュ方程式から運動方程式が求まる。

座標系によらない定式化を試みた！ってことです。

参考図書

いくつかおすすめの解析力学の参考書を挙げておきます。

ランダウ力学

力学 (増訂第3版) ランダウ=リフシッツ理論物理学教程

エリ・ランダウ, イェ・エム・リフシッツ

2,200円(11/21 22:15時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

下記のような小教程もあります。

力学・場の理論―ランダウ=リフシッツ物理学小教程 (ちくま学芸文庫)

L.D.ランダウ, E.M.リフシッツ

1,650円(11/21 16:46時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

解析力学：マセマキャンパスゼミ

解析力学キャンパス・ゼミ改訂3

馬場敬之

4,480円(11/21 11:20時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

↑こちらは「スバラシク実力がつくと評判」シリーズの解析力学の参考書です。
著者は高校数学を教える予備校の講師で、とてもわかりやすいと評判です。
その方が書いた書籍なので高校生でも読みこなすことができるくらいわかりやすく、かつちゃんと大学の物理の内容を扱っています。

解析力学ⅠⅡ：朝倉物理学大系

解析力学1 (朝倉物理学大系)

義隆, 山本, 孔一, 中村

6,160円(11/21 11:20時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

解析力学2 (朝倉物理学大系)

義隆, 山本, 孔一, 中村

6,380円(11/21 11:20時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

この2冊は解析力学の名著ですね。
数学的な解説も多く、解析力学を深く学ぶ人には挑戦するには申し分ない内容です。

詳解力学演習

2,750円(11/21 11:20時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

こちらは「力学」と「解析力学」の演習問題を扱っている演習問題集になります。

POSTED COMMENT

サトウより:

2018年4月6日 08:27

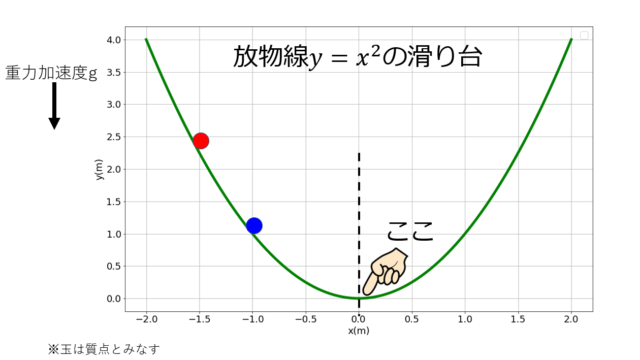
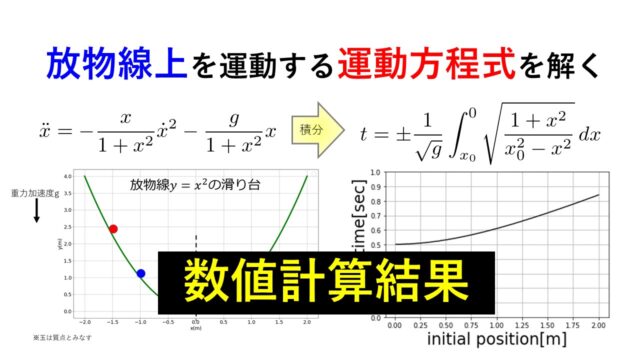
部分積分変形後の積分の項で()の外にδqiをつけ忘れてませんか？

返信
- korokoro より:
  
  2018年4月6日 09:17
  
  本当ですね。修正致しました。
  δqiを忘れているのは、まずいですね。一番肝心なところが抜けていました。
  どうもありがとうございます。
  今後ともよろしくお願い致します。
  
  返信
伴　公伸より:

2019年6月13日 16:29

　伴　公伸といいます。はじめまして
　ファインマンの経路積分で特定経路以外の経路成分は互いに打ち消しあい経路積分に寄与しないその　根拠が最小作用の原理だそうだ。そうですか、？
　そうとするとそれはホワイトノイズの学理に矛盾するんです。
　ファインマンの経路積分は３次元の空間を自由に通る曲線経路についての計算ですが、1次元の直線線分を経路にしてやると、通信工学でよく使われる周波数特性グラフを求めるときのフーリエ積分と同形のオイラー関数を積分核にした積分計算になります。
　その値ですが、もし波動が確率的に変動すると積分の結果は中心極限定理からホワイトノイズになることが学理に証明されています。
　ところがホワイトノイズの定義から、ファインマンの経路積分に起きたような打ち消しあい積分に寄与しない成分は存在しません。
　したがってファインマンの経路積分での打消し合い寄与を減らす原因の働きは別に存在し、そこに最小作用の原理を生み出す親が潜んでいます。
　最小作用の原理はすべての物理現象に共通して働いている。ならば親はすべてを生み出す根源的存在ということです。
　親は私が睨んだところ、波動の引き込み現象です。
機会があったら私を探して、討論してみませんか。
　

返信
itohideki より:

2020年6月27日 20:26

はじめまして．伊藤英樹と申します．大学で学んだ物理学（一般力学）を復習していてこのサイトを見つけました．とても勉強になりました．ラグランジェ？ルジャンドル？　と混同しているレベルですのでまだまだ勉強不足ですが．ありがとうございました。

返信
- korokoro より:
  
  2020年6月27日 23:48
  
  コメントありがとうございます。
  大変うれしく思います。
  これからもよろしくお願いします。
  
  返信
mango より:

2022年9月17日 21:05

部分積分の前に項はあってはならないように

返信