こんにちは(@t_kun_kamakiri)(^^)/
前回の続きです(^^)/
↑こちらで、「ランダウ=リフシッツの”力学”読んだら物理で絶望するよ」という記事を聞きました。
ランダウ=リフシッツの”力学”の教科書は「力学」ではなく「解析力学」です。
解析力学の立ち位置は、ニュートン力学をより美しく一般的な形式に従って運動を記述できるようにした学問である。
本記事の内容についてはこちら。
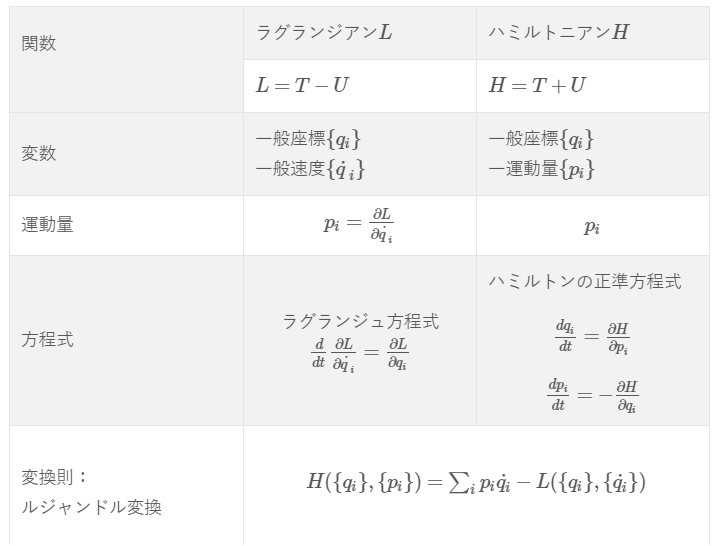
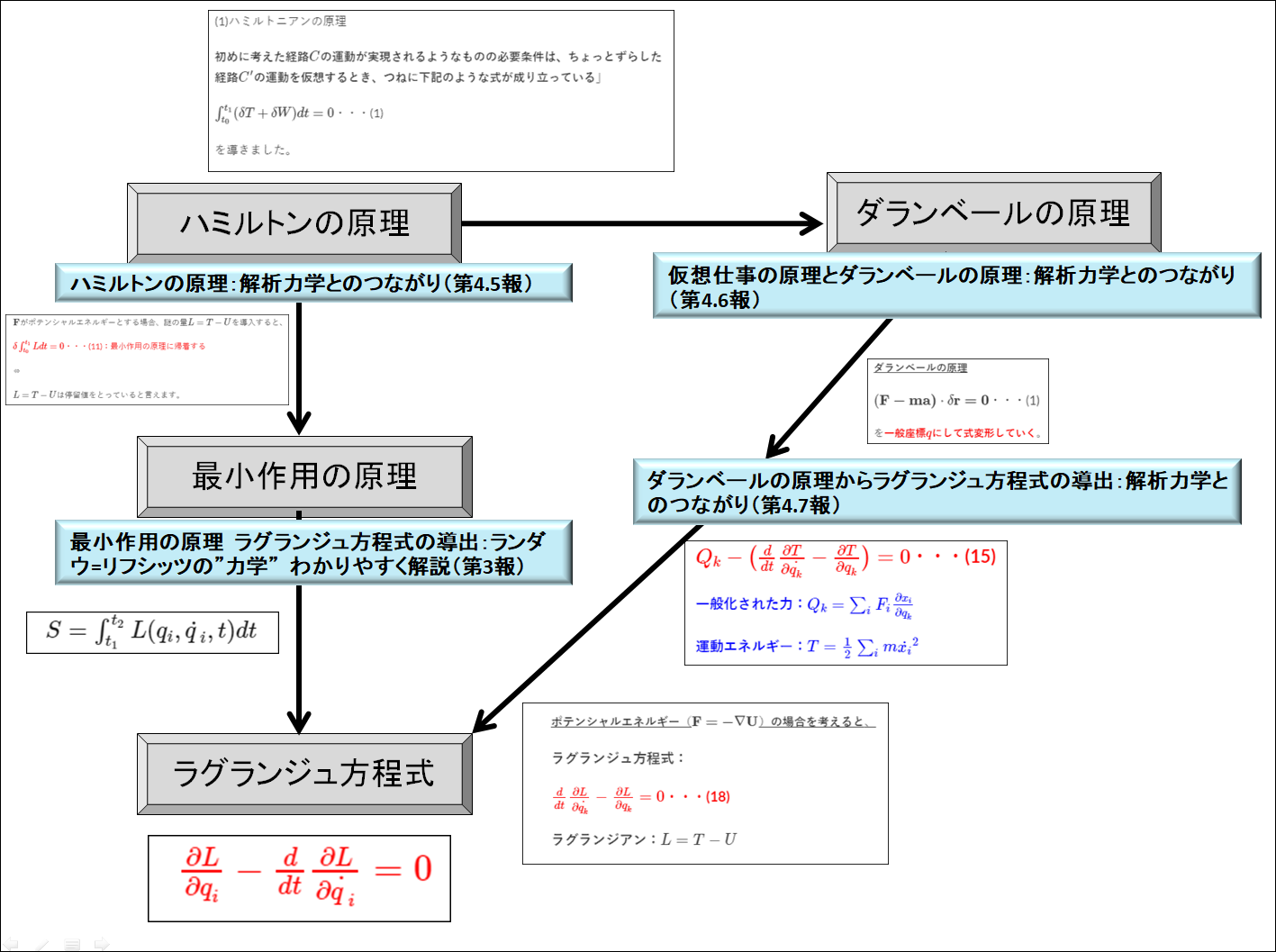
ラグランジュ方程式
※ラグランジアン\(L\)
を導くにあたって一般化座標というのを導入します。
ラグランジュ方程式を導く前段階の一般化座標についてお話したいと思います
では、内容に入りたいと思います(^^)/
座標系を変えると見た目が変わる。それは「面倒だな」から・・はじまる。
「ランダウ=リフシッツの力学」では、いきなり一般化座標系のお話をし始めて面喰います。なぜこのような話から入るのか?
一般的な形式に従って運動を記述できるようにしたいからです。
たとえば、デカルト座標系\((x,y,z)\)で運動を記述したい場合は、運動方程式を次のように書きます。
デカルト座標系での表記
\left\{\begin{matrix}
(x方向)&m\frac{d^{2}x}{dt^{2}}=F_{x}\\
(y方向)&m\frac{d^{2}y}{dt^{2}}=F_{y}\\
(z方向)&m\frac{d^{2}z}{dt^{2}}=F_{z}
\end{matrix}\right.
\end{align*}
このようになりますね。
でも、別に\((x,y,z)\)を基準座標にせずとも、直行した3つのベクトルを基準にした座標系であれば運動を記述することができるのです。
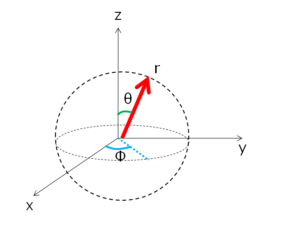
例えば、3次元極座標系\((r,\phi,\theta)\)でも良いのです。
3次元極座標系での表記
※下記の導出は別途記事を上げます。ここではひとまずこういうものかと思っておきましょう。
\left\{\begin{matrix}
(r方向)&m\big(\ddot{r}-r\dot{\phi}^2\sin^2{\theta}-r\dot{\theta}^2)&=&F_{r}\\
(\theta 方向)&m\big(r\ddot{\theta}+2\dot{r}\dot{\theta}-r\dot{\phi}^2\sin{\theta}\cos{\theta})&=&F_{\phi}\\
(\phi 方向)&m\big(r\ddot{\phi}\sin{\theta}+2\dot{r}\dot{\phi}\sin{\theta}+2r\dot{\theta}\dot{\phi}\cos{\theta})&=&F_{\theta}
\end{matrix}\right.
\end{align*}
※\(\frac{dr}{dt}=\dot{r}\)、\(\frac{d^2r}{dt^2}=\ddot{r}\)
上の2つの座標系での運動方程式を見てお分かりのように、座標系を変えるだけで同じ現象を記述しているつもりが、全くもって別の形式になってしまいました。
これらをもっと統一的に記述できるようにできないか?といった一般的な形式を探索したのが解析力学です。
一般化座標って?
先ほどのお話の続きですが、もっと一般的な座標で”状態”を記述できないか?
その力学的な状態は何で決まるのか?
結論を下記に示します。
以降で順を追って説明します。
一般化座標
位置座標をデカルト座標系や極座標系に絞ると、形式が変わってしまうので、とりあえず一般的な座標として文字を\(q_{i}\)と置きます。
座標系の名前は何でも良いので、“なんちゃら座標系”にしておきます。
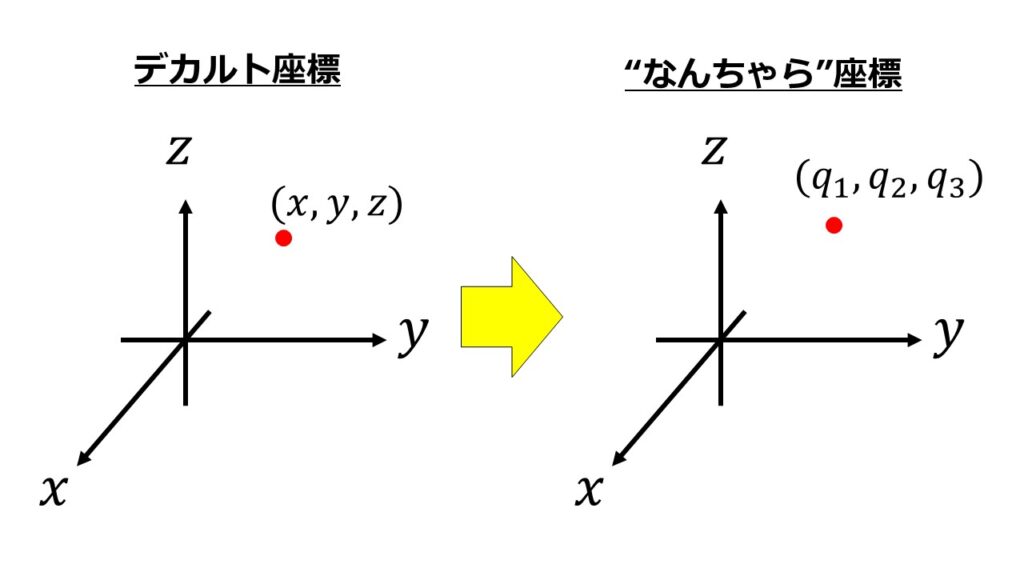
この”なんちゃら”座標系には「デカルト座標系」「円筒座標系」「極座標系」など色々ありますが一般化座標として$q_{i}(i=1,2,3)$と表すことにしましょう。
※粒子がN個存在し、3次元である場合、\(i=3N\)になります。
この独立な量の個数を系の自由度と言います。
一般化速度
その時刻における位置だけで状態は決まるのか?
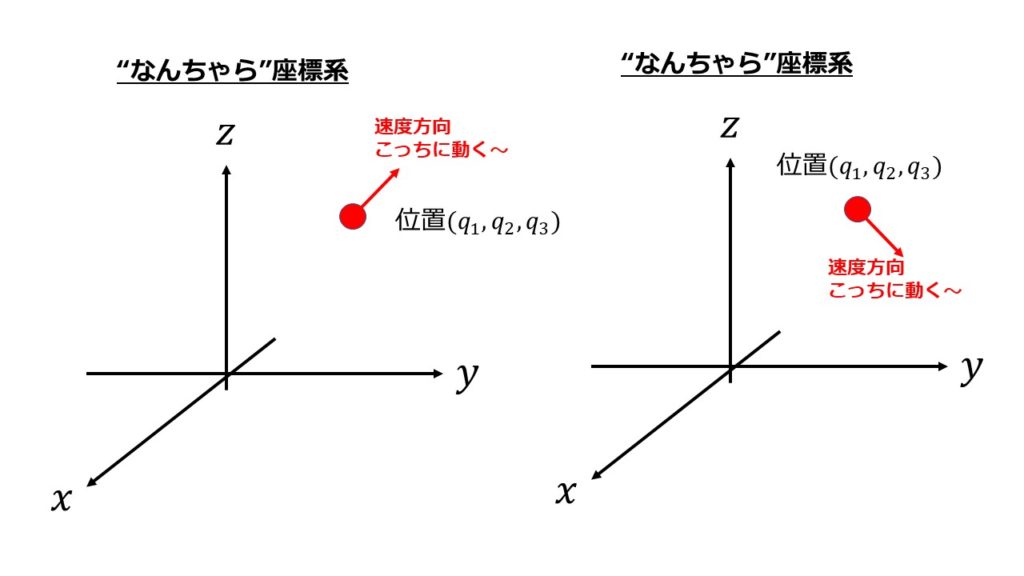
たとえ同じ位置だとしても、その位置での速度が異なる場合はそれ以降の質点(粒子)の運動は異なることになります。
だから、位置(座標)以外に速度も力学的な状態を決定するのに必要であると言えます。
位置座標\(q_{i}\)を一般化座標にしたように、ここでも速度を一般化座標の導関数として一般化速度\(\dot{q}_{i}\)を定義することにします。
座標系によらない一般論を論じましたね!(^^)!
- 一般化座標$q_{i}$
- 一般化速度$\dot{q}_{i}$
そして、「ランダウ・リフシッツの”力学”」にはこのような記述があります。
実に深いですね。
原理的に予言できるという記述が気になります。
N\(\simeq10^{23}\)個のアボガドロ数個の運動方程式立てれば粒子の運動を記述できるじゃないか・・・これは、原理的にできる!!
だが、できない!!
できたとしても意味がない(笑)
なぜなら、それだけ多くの情報のある答えを導き出しても、どう解釈すればいいかこちら側が判断できないとでも言いたげですね。
現に、そういう発想を起点に統計力学という分野があるのですからそうなのでしょう。
まとめ
ラグランジュ方程式を導くにあたって、一般化座標というのを導入しました。
ある時刻における一般化座標\(q(t)\)と一般化速度\(\dot{q}(t)\)により力学的な状態が決まり、それ以降の運動を予言できます。
座標系によらない一般的な形式を探索しましょうといスタンスを垣間見れたかと思います。
次回
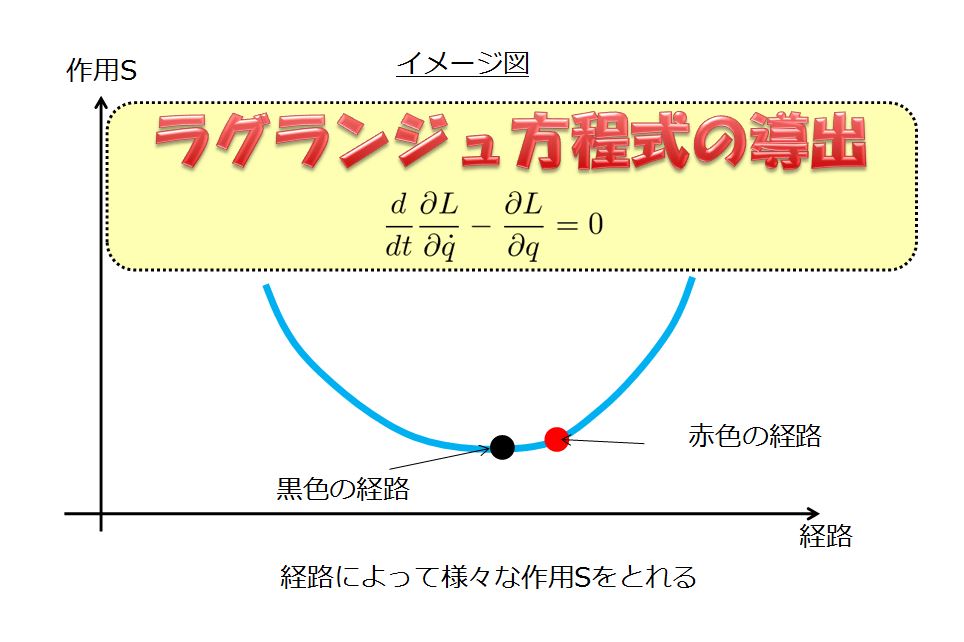
次回は、「最小作用の原理」というお題です。
いよいよラグランジュ方程式を導きます(^^)/
↓これです。
ラグランジュ方程式
\frac{d}{dt}\frac{\partial L}{\partial \dot{q}}-\frac{\partial L}{\partial q}=0\end{align*}
※ラグランジアン\(L\)
参考図書
いくつかおすすめの解析力学の参考書を挙げておきます。
ランダウ力学
解析力学:マセマキャンパスゼミ
↑こちらは「スバラシク実力がつくと評判」シリーズの解析力学の参考書です。
著者は高校数学を教える予備校の講師で、とてもわかりやすいと評判です。
その方が書いた書籍なので高校生でも読みこなすことができるくらいわかりやすく、かつちゃんと大学の物理の内容を扱っています。
解析力学ⅠⅡ:朝倉物理学大系
この2冊は解析力学の名著ですね。
数学的な解説も多く、解析力学を深く学ぶ人には挑戦するには申し分ない内容です。
詳解 力学演習
こちらは「力学」と「解析力学」の演習問題を扱っている演習問題集になります。