物理ネタの初投稿です。
と言ってもめーっちゃ難しい話をするのではなくて、物理って以外に感覚が大事なんじゃないか?
そんな話をしたいと思います。
お題は、「バスケットボールのシュートが全然飛ばなーーーい。」
って人のために、ちびっとでも役に立ちたいと思っています。
ボールの飛距離が出ない原因は何か?
- ボールの軌道が悪い
- ボールに回転がない
- シュートフォームが変
- 足を使えていない
そりゃー原因を上げればきりがないのやけども、物理的に解説できるのは、
「1.ボールの軌道が悪い」
「2.ボールに回転がない」
ですかね。
そして、今日は「1.ボールの軌道が悪い」だけを取り上げて、
同じ速度でボールを投げた時、どういう角度なら一番ボールの飛距離が伸びるのか?を高校物理の知識で解説したいと思います。
簡単のために、上記の絵で解説します。
実際これだったら、あんた身長何cm?ってなるが・・・
物理はとても感覚が大事
物理の現象は難しい数式で書かれることが多いですが、数式を解いて出された答えが今までの日常で感じている”感覚”とずれていると、「ん?計算間違いしたかも?」ってなるんです。
逆に、「きっと何となくこうだろうな」と思った感覚は、だいたい当たっているのです。
次の絵を見てください。
例1
ボールをほぼ水平方向に、「うりゃっ」って投げた場合、すぐ下に落ちてしまいますよね。
逆に、
例2
「そーれっ!」って上方向に向けてボールを投げると、高い軌道を描くが、飛距離は伸びない。
はて?どちらがいいの????
答えは、真ん中:つまり、\(\theta=45°\)
これです。後で、式で示します。
物理の数式が嫌だっていう人は、ここまでにしてその感覚をどんどん磨いていけばいいんです。
でも、せっかく物理を勉強したから、ちょっと数式を解きながら理解したい人は、高校物理でこんなことを習ったと思います。
それが次です。
\(\theta=45°\)で最も飛距離が伸びるのを数式で導こう
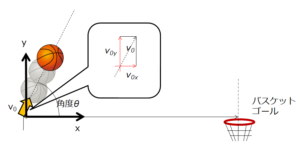
初速度\(v_{0}\)とします。
ここで、\(v_{0x}=v_{0}\cos\theta\)、\(v_{0x}=v_{0}\sin\theta\)と書けるので、
- x方向のボールの距離について
\(x=v_{0x}t\)・・・①
- y方向のボールの距離について
\(y=v_{0y}t-\frac{1}{2}gt^{2}\)・・・②
\(y=0\)のとき、\(x\)が最大となる\(\theta\)を探せばよいのですから、
②の\(y=0\)として、①を代入し\(t\)を消去しましょう。
すると、
\(x=\frac{2v_{0x}v_{0y}}{g}=\frac{\sin2\theta}{g}\)
\(0\leq\theta\leq90°\)の範囲であれば、\(\theta=45°\)で\(x\)が最大になる。
まとめ
- やっぱり感覚とずれていなかった!(^^)!
- 厳密には、打ち出し位置のy座標と、バスケットゴールのy座標が同じであったので、簡単に数式でできたけど、打ち出し位置とバスケットボールの高さが違う場合はどうなの??
- ボールに回転がかかった方が飛距離が伸びるんじゃないか?
2、3については別の記事でアップしたいと思います。
最後まで読んでいただいてありがとうございました。
こちらに簡単なプログラムを作って検証してみましたのでご覧ください(^^)