こんにちは(@t_kun_kamakiri)
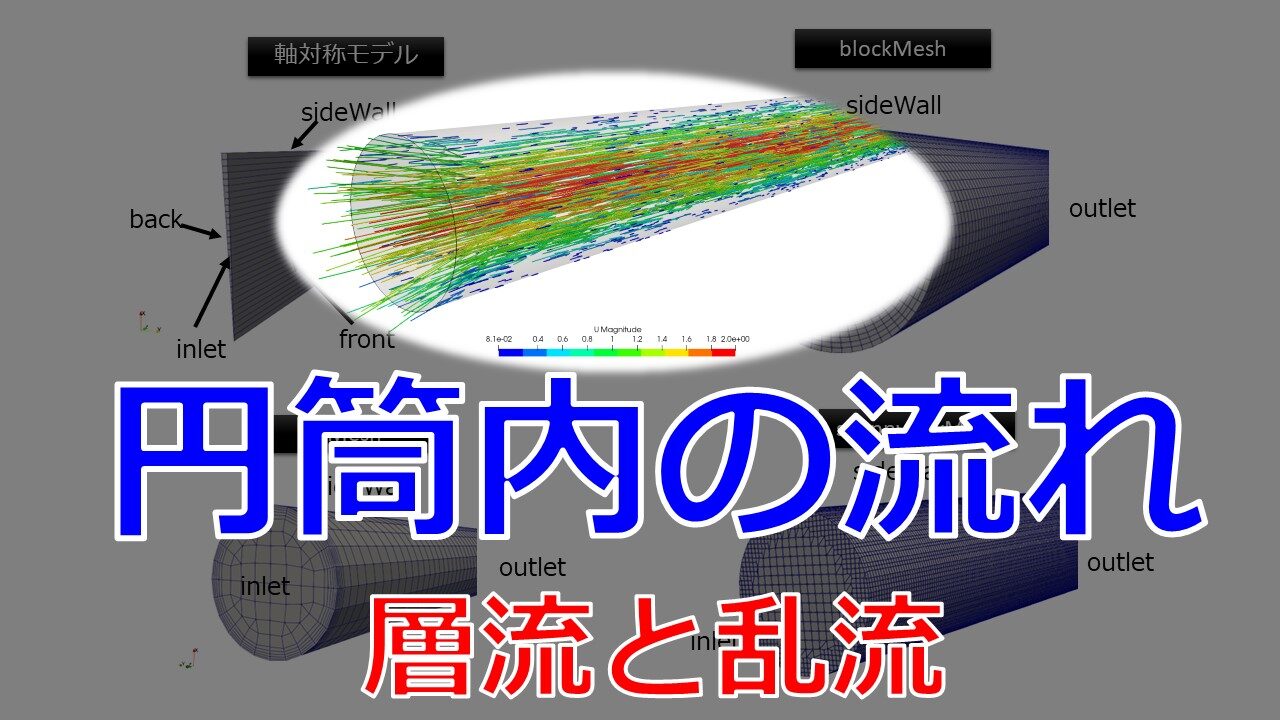
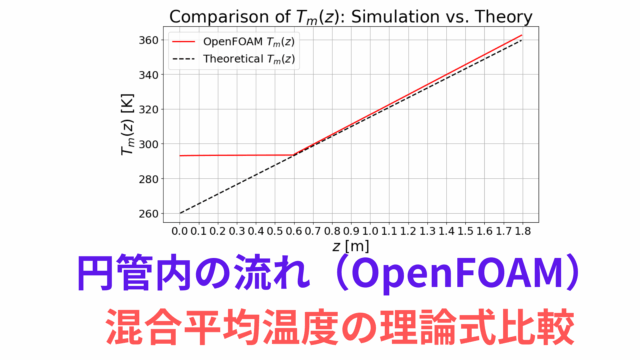
今回の記事では円筒内の流れをOpenFOAMでやってみたという内容です。
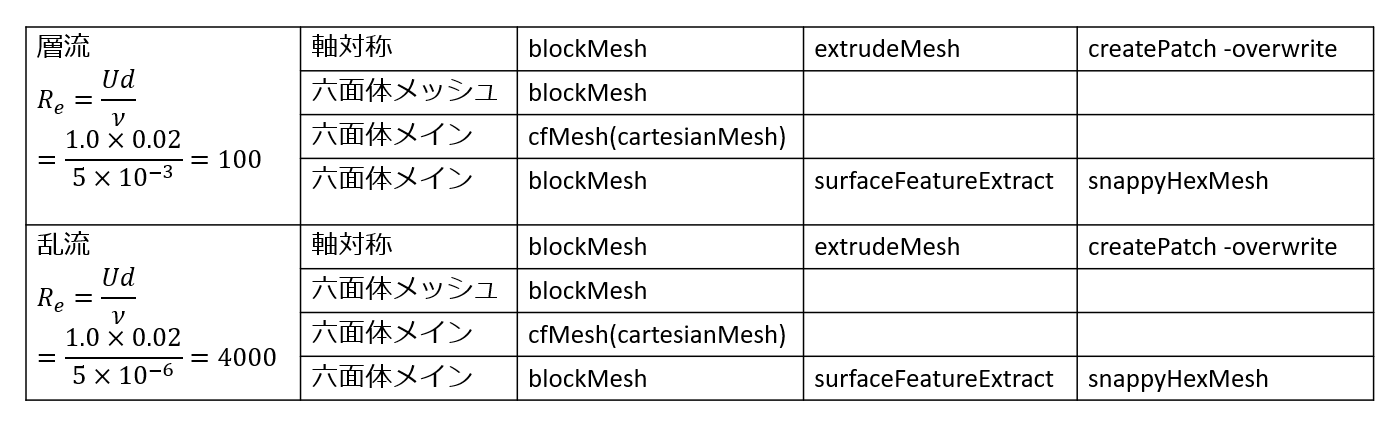
4パターンの異なるメッシュの作り方で解析を試してみました。
メッシュの作り方については↓こちらをご参考ください。
円筒内部の流れは理論的にもよく理解されている基本的な流れですね。
- レイノルズ数の大きさによる層流・乱流遷移
- 層流と乱流の助走区間の違い
- 層流と乱流の速度分布の違い
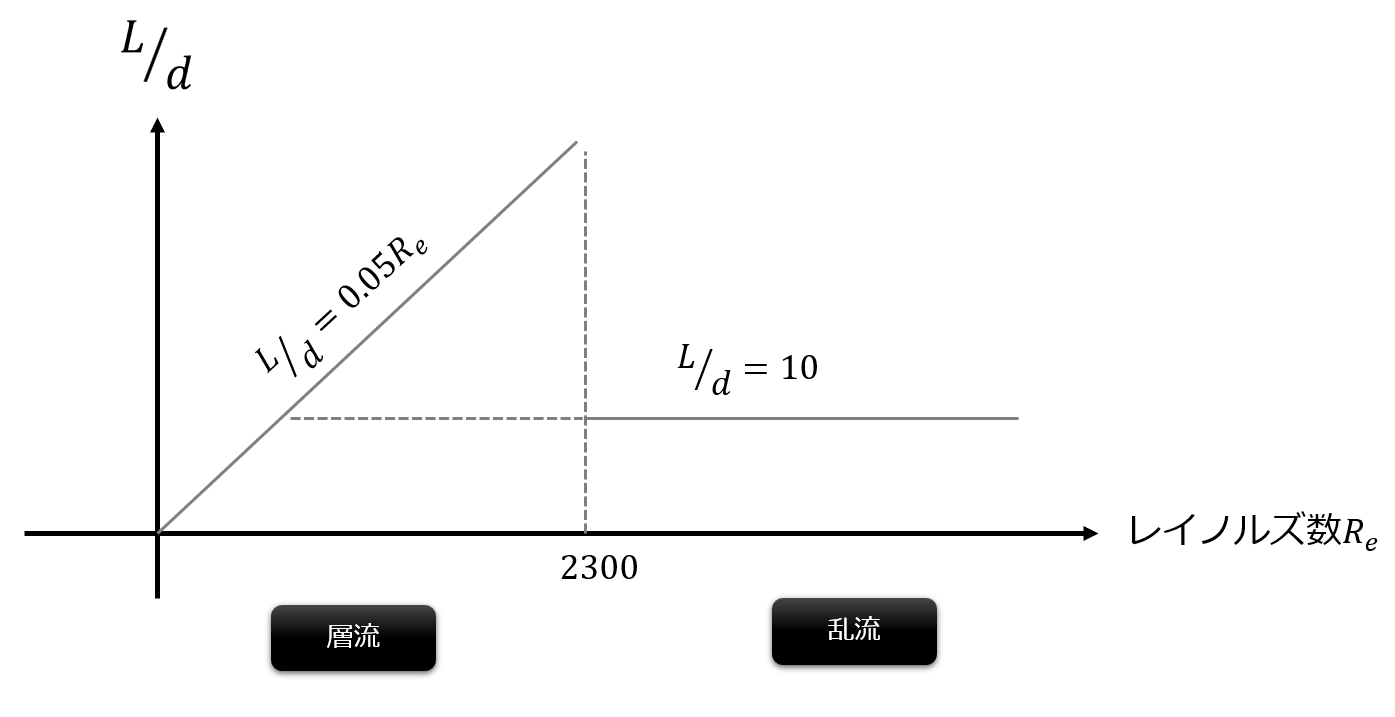
層流と乱流の助走区間の距離$L$違いについては、直径$d$との比率で決まります。
層流では$\frac{L}{d}=0.05Re$とレイノルズ数に比例して十分発達するまでの距離が決まり、乱流になると$\frac{L}{d}=10$とレイノルズ数に依存せずに決まります。
これらの内容は流体力学の参考書にもある話です。
流体のシミュレーションをしていると何となく結果はでるけども「あってるのどうなの?」と思うこともしばしばあります。
実験とシミュレーションの結果を比較するというのもひとつの手ではありますし、流体力学の中でも条件を限定すると解析解を導くことができ、シミュレーションとの比較を行うことができます。
解析解もシミュレーションもどちらも理論に基づくものなので、両者は一致しないといけません。今回はシミュレーションが正しく行えているのかを確認するために、円筒のモデルを作成して流体解析を行い、解析解とシミュレーションとの比較を行うことにします。
OpenFOAMv2012(WSL)
Python3.8.5
モデル作成
メッシュ作成は前回の記事で終えているので解析条件を設定します。
今回行う解析はΦ20×200の円柱内の流れで、メッシュパターンは以下の4パターンで行います。
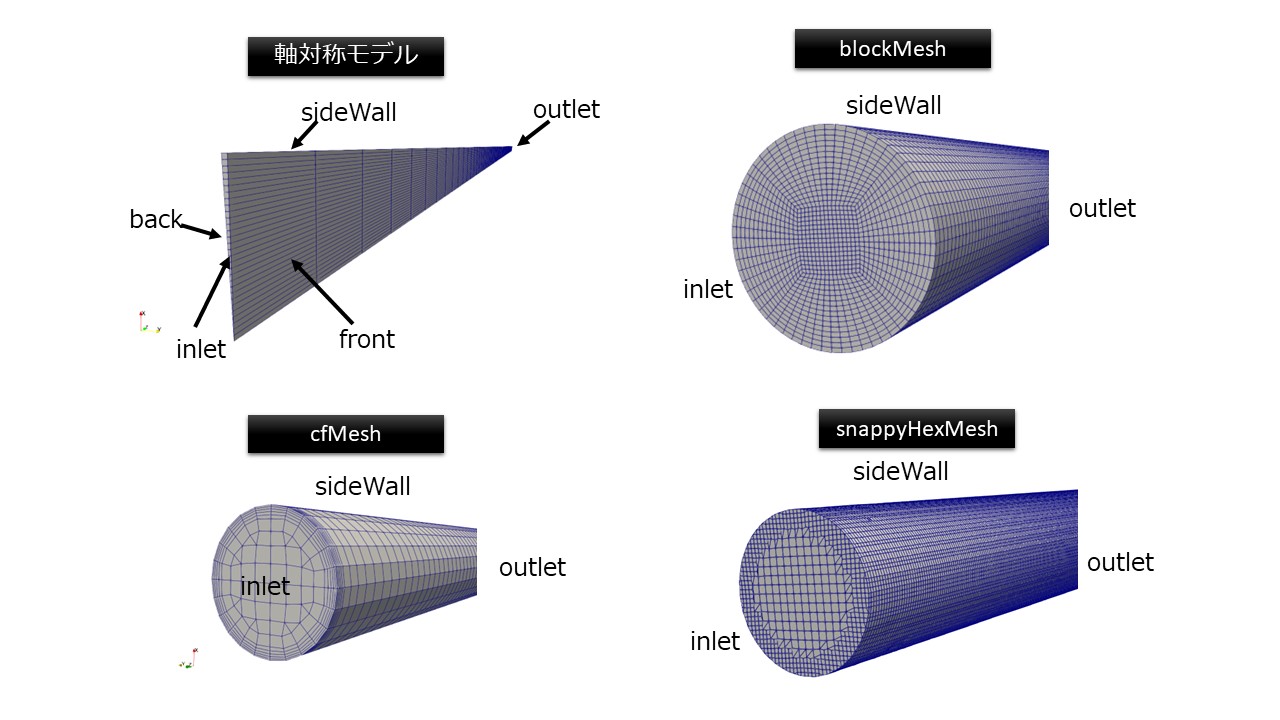
層流と乱流の速度分布の違いを見るために、助走区間の距離を考慮してモデルを作っています。助走区間は層流において十分に発達するまでの距離が長いので、大きくとる必要があります。
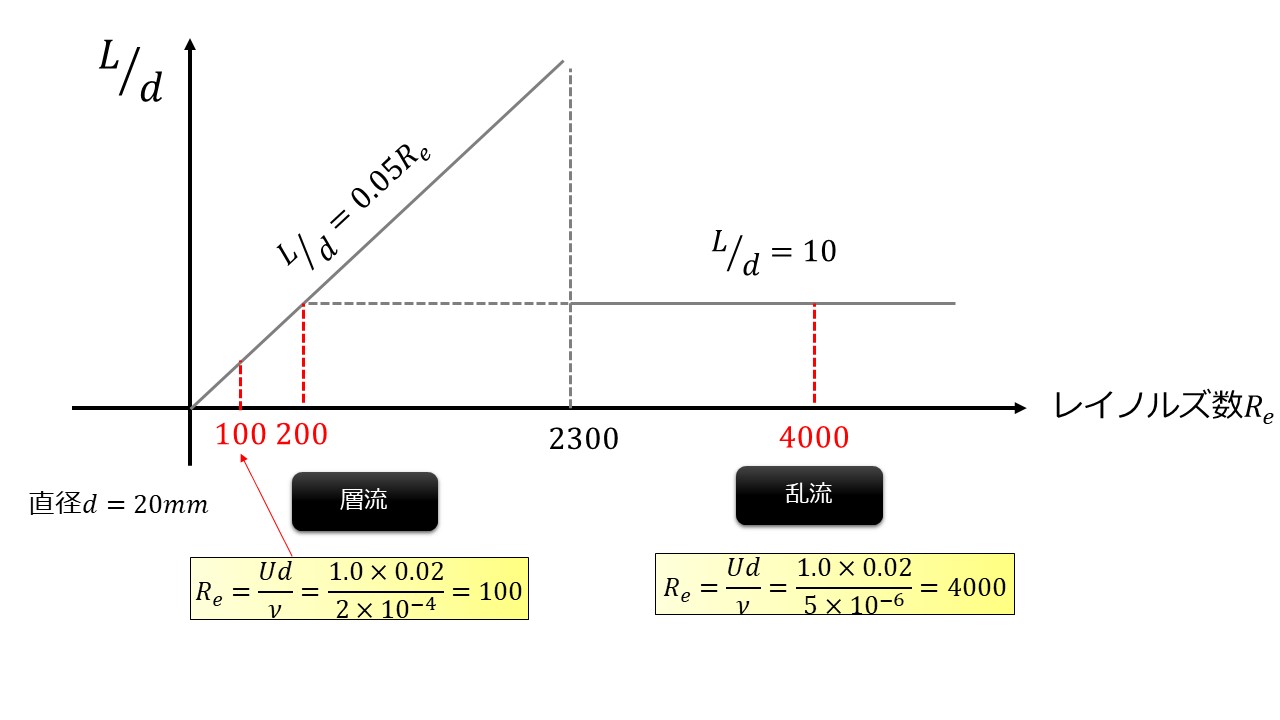
乱流状態と同じモデルにするために$Re=4000$での乱流状態での助走区間は$d=20$mmとすると$\frac{L}{d}=10$より、$L=200$mmとなります。
層流において
助走区間の距離$L=200$mmとすると$\frac{L}{d}=0.05Re$よりレイノルズ数$Re=200$なります。念のため助走区間をもっと短くするためにレイノルズ数を小さくして$Re=100$にして解析を行います(この方がより層流側の流れになるため理論値と一致した)。

これによりモデルの円筒の長さは最低200mmにすれば良いことがわかります。
メッシュの作り方で試してみると勉強になりますね。
モデルの保存先
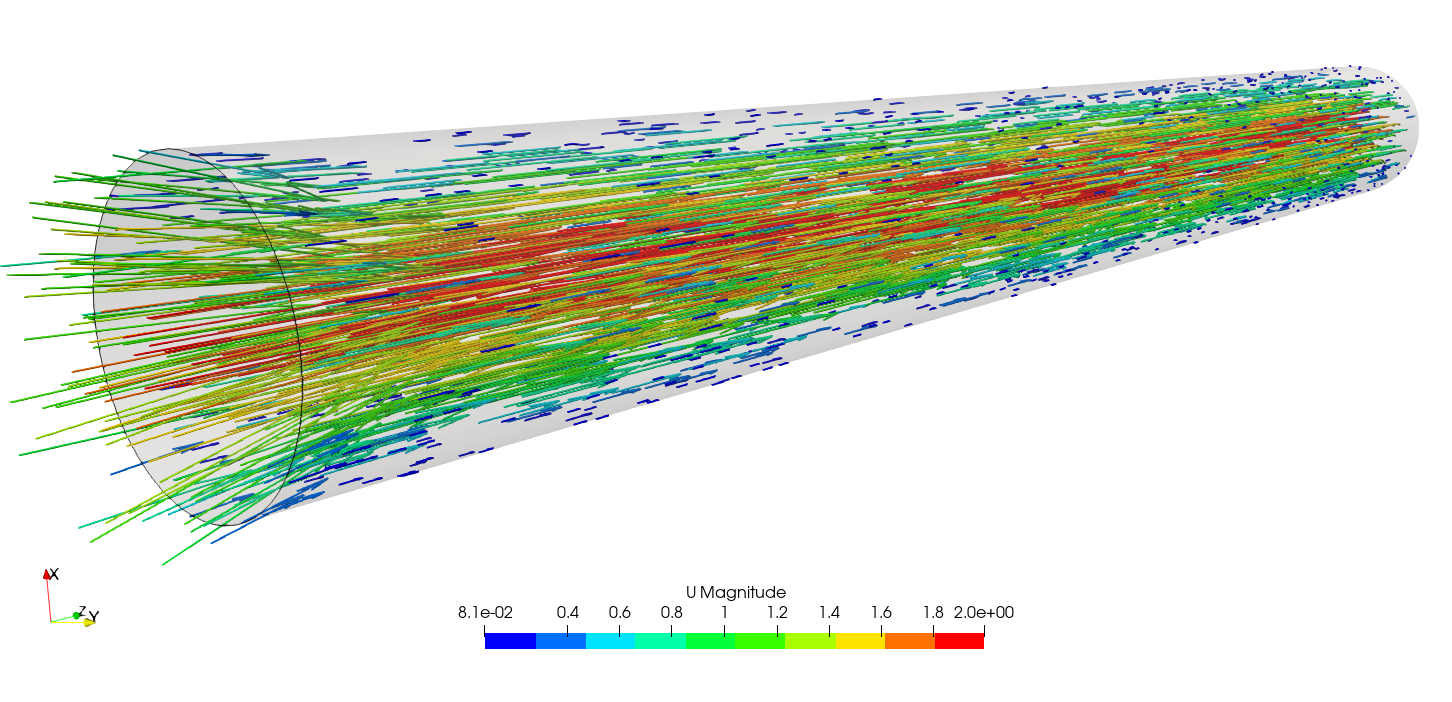
流れはこんな感じです。
円筒内の流れの理論式
助走区間の距離も十分にとり、十分発達した流れの速度分布は軸方向に変化をしないから$\frac{\partial u_{z}}{\partial z}=0$,$u_{x}=u_{y}=u_{r}=0$(半径方向の流速0)となります。
u_{z}\frac{\partial u_{z}}{\partial z}+u_{r}\frac{\partial u_{z}}{\partial r}=-\frac{1}{\rho}\frac{\partial p}{\partial z}+\nu\frac{1}{r}\frac{\partial }{\partial r}\bigg(\frac{\partial u_{z}}{\partial r}\bigg)
\end{align*}
※今回は$z$方向が流路軸方向です。
$\frac{\partial u_{z}}{\partial z}=0$,$u_{x}=u_{y}=u_{r}=0$のとき、
0=-\frac{1}{\rho}\frac{\partial p}{\partial z}+\nu\frac{1}{r}\frac{\partial }{\partial r}\bigg(\frac{\partial u_{z}}{\partial r}\bigg)
\end{align*}
となるので、両辺$r$で積分して、
u_{z}&=\frac{1}{4\mu}\bigg(-\frac{\partial p}{\partial z}\bigg)\big(R^2-r^2\big)\\
&=2u_{b}\bigg(1-\big(\frac{r}{R}\big)^2\bigg)
\end{align*}
となります。
※$\nu=\frac{\mu}{\rho}$
ここで、$u_{b}=\frac{1}{\pi R^2}\int^{R}_{0}2\pi r u_{z}dr=\frac{R^2}{8\mu}\big(-\frac{\partial p}{\partial z}\big)$の平均流速を導入しています。
グラフにまとめる
Pythonのプログラムで層流と乱流での流速分布の比較を行いました。
また、層流に関しては理論式が近似的に導かれるのでその比較も行っています。
層流の場合の円筒内の流れの近似式はこちらです。
u=2u_{b}\bigg(1-\big(\frac{r}{R}\big)^2\bigg)
\end{align*}
$u_{b}$は円筒断面の平均流速です。
流入速度を一定値$1.0$[m/s]としているのでその値を与えています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 |
import re import numpy as np import matplotlib.pyplot as plt import pandas as pd import subprocess import os, shutil from pathlib import Path # 文字列を含む要素を数字で昇順にする関数 def atoi(text): print(text) return int(text) if text.isdigit() else text def natural_keys(text): return [ atoi(c) for c in re.split(r'(\d+)^', text) ] # 数字であるかどうかの判定 def is_int(s): try: int(s) return True except ValueError: return False def graph_plot(clyndeMeshType): # 計算パターンのリスト resultDir_list = [d for d in os.listdir("./") if clyndeMeshType in d] # グラフのセット fig, axes = plt.subplots(1, 4, figsize=(24,8), tight_layout=True) # colorの設定(laminar=>red, turbulence=>blue) color_list = ["red","blue"] Radius = 10/1000 # 半径 10mm = 0.01m ub = 1.0 # 断面平均速度(流入速度1.0m/s) y = np.arange(-1,1,0.01) uy = 2*ub*(1-y**2) for j, resultDir in enumerate(resultDir_list): resultDir = Path(resultDir) # 計算フォルダ latestTime = sorted([a for a in os.listdir(resultDir) if is_int(a)], key=float)[-1] # latestTimeを抜き出す print(latestTime) sampleDictdata = resultDir/"postProcessing"/"sampleDict"/latestTime # ファイル名を数字部分と非数字部分に分割するための正規表現パターン pattern = r'(\d*\.\d+|\d+)' # 数字部分だけを抜き出して、数値に変換してソートする caseList = sorted(os.listdir(sampleDictdata), key=lambda f: [float(d) if d.isdigit() else d for d in re.split(pattern, f)]) for i, zCase in enumerate(caseList): if j ==0 :axes[i].plot(uy, y, color="black", label="Theory") df_data = pd.read_table(sampleDictdata/zCase, index_col=False, names=('x[m]', 'y[m]', 'z[m]', 'Ux[m/s]', 'Uy[m/s]', 'Uz[m/s]')) axes[i].scatter(df_data["Uz[m/s]"], df_data["x[m]"]/Radius, color=color_list[j], label=f"{resultDir}") axes[i].set_ylabel("y[m]", fontsize=16) axes[i].set_xlabel("Uz[m/s]", fontsize=16) if i>=3: plt.legend(loc="upper center",bbox_to_anchor=(1.5, 1.0), fontsize=12) axes[i].grid("-") axes[i].set_title(f"z={zCase.split('_')[1]}", fontsize=20) plt.savefig(f"{clyndeMeshType}.png") # ================ main =================== clynderMeshTypeList = [ "Cylinder_axialSymmetry", "Cylinder_blockMesh", "Cylinder_cfMesh", "Cylinder_snappyHexMesh" ] for clyndeMeshType in clynderMeshTypeList: graph_plot(clyndeMeshType) |
こちらを実行すると以下のようにグラフ化されます。
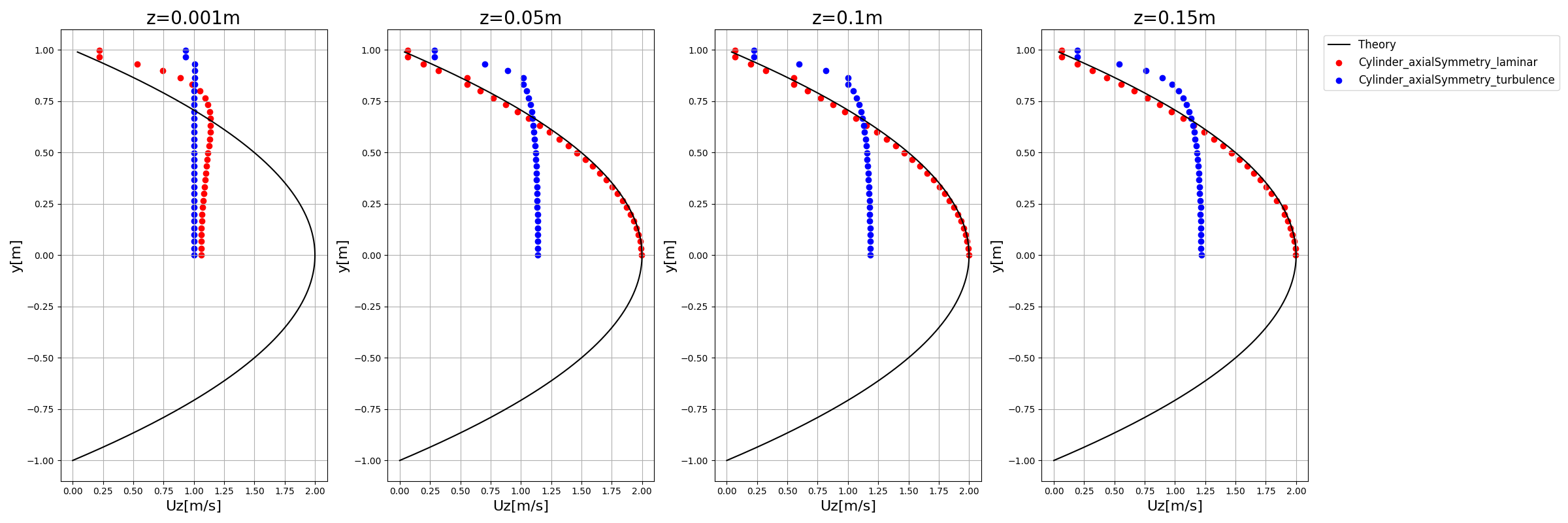
軸対称モデルでの結果
【OpenFOAM(円筒内の流れ)】軸対称モデルでメッシュ作成(4)
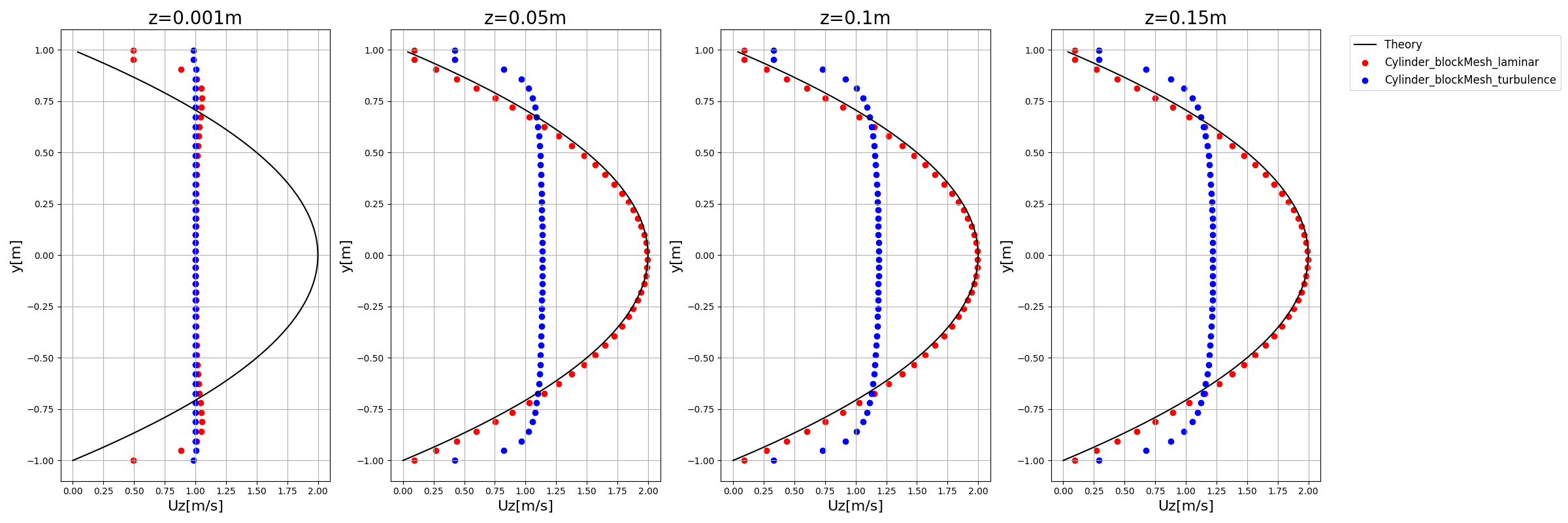
blockMeshでの結果
【OpenFOAM(円筒内の流れ)】blockMeshでメッシュ作成(1)
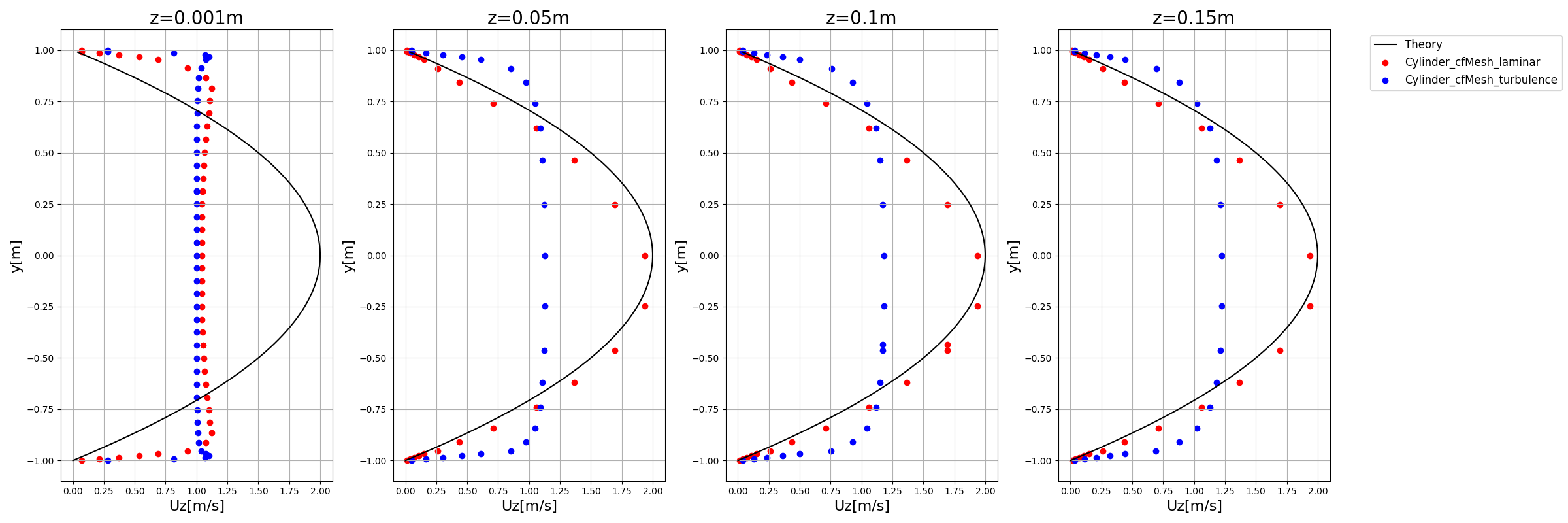
【OpenFOAM(円筒内の流れ)】cfMeshでメッシュ作成(3)
【OpenFOAM(円筒内の流れ)】snappyHexMeshでメッシュ作成(2)
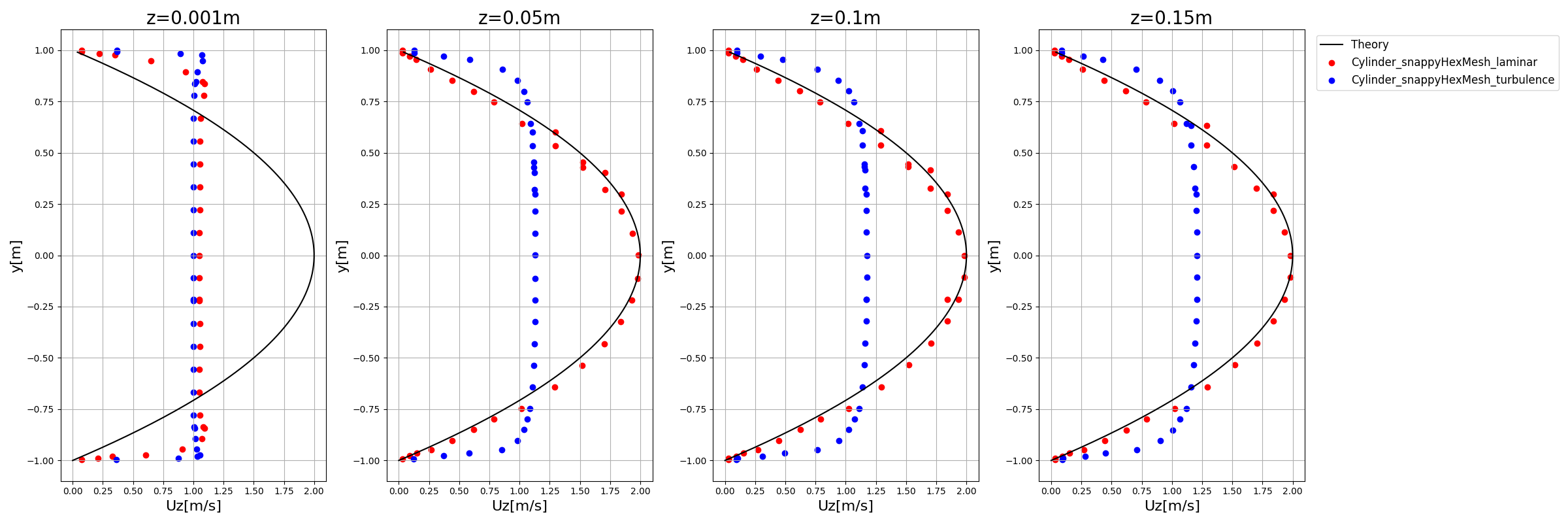
もう少しメッシュ数増やすなりすれば改善するかもしれません。
また、乱流と層流で速度分布が全然違うというのも円筒内流れの特徴ですね。
まとめ
今回はメッシュの作り方違いで円筒内流れをOpenFOAMで解析してみました。
また、層流と乱流での速度分布の違いをPythonでグラフ化して確認しました。
基本的な解析内容ですが、教科書的な内容で良い勉強になりました。
おすすめ参考図書
☟こちらは、OpenFOAMの日本語書籍として重宝しているわかりやすい参考書だと思います。
☟こちらもOpenFOMの古いバージョンでの和訳になります。さすがにこちらはバージョンに対する日本語でのケアはしていないので、OpenFOAMに慣れている方は購入しても良いかと思います。僕は「日本語でまとまっている内容」なので少し重宝しています。
☟以下に、もっと初心者向けの同人誌を紹介しておきます。
初心者は「ってか、まずどうやってOpenFOAMをインストールするの?」というところからつまずきがちです。
そんな時は、以下の書籍をおすすめします。
インストール方法とチュートリアルで流体解析を体験・・・ちょっと高度な解析まで解説があります。著者曰くOpenFOAMのバージョンの追跡を行いながら、書籍をアップデートするようなので安心ですね。