【CAE解析の目的とは？】CAEは実機の代替えなのか？精度を無視してパラメータスタディすることは意味がないのか？

こんにちは（@t_kun_kamakiri）

僕は、2016年からCAE解析を経験しているのですが、ふと・・・・・

と、疑問に思うことがあります。

「何でもCAEで解析できないか？」という依頼が来るのを、めんどうに思ったからです(‘ω’)

と、思うこともあるのです。

そんなこともあって、本記事は改めてCAE解析を使う目的などの個人的な考えを語っていこうと思います(^^)/

※目的は「その人の状況や立場（すべてをひっくるめて環境）」に依存するため、最後の結論（目的）は当然立場によって変わります。

ですので、目的は立場によって自分なりに設定する必要があります(‘ω’)

CAEの精度を無視してパラメータスタディすることは意味がないのか

このようなことを発言をする人がたまにいます。

そうしたときにいつも思うのは、

なぜ、このような押し問答みたいなやりとりになるのでしょうか？

それは、

であると考えています。

CAEを使う目的とは何か？

CAEという略語から説明した方がわかりやすいかもしれません。

つまり、「コンピューターによる技術支援」なのです・・・CAEは。

この言葉の意味（CAEは技術支援であること）から、「CAEを使う目的」を考え直す必要があると考えています。

製品の設計の際には必ず強度設計というものをすることでしょう。

その際に、例えばCAEがないものと考えた時に、手計算で「ここにはこれくらいの応力が生じている」など強度を見積もったりするでしょう。

その時に、応力の見積もりだけ知れば良かったのでしたっけ？

どういった設計値が、どれくらい応力に影響しているかも把握したくはないでしょうか？

つまり、こういうことです、

これは非常に重要な見解です。

知りたいこと（応力など）に対して、何がどれくらい影響しているかというのを知ることはとても重要です。

しかし、手計算でできるレベルというのは非常に単純化されていることが多いのです。

ゆえに、実際の形状とは違うので実機と理論は合っていないことになります（実際に合っていないことが多い）

ですが、実機と合っていなくても理論から得られた見解はとても重要な知見として重宝されるはずです。

CAEに対する誤解：CAEは神様なのか？

CAEはとても実物に近い形を再現してくれます。

「見た目が実際を再現しているから、実機とCAEは必ず合う」などの誤解があるからか、とんでもないハードルの期待値をかけてしまっている人を散見します。

それゆえに、CAEと実機が合っていなかったらCAEは意味がないなどと誤解されてしまいがちです。

CAEはそんな神様みたいなものでもないのです。

CAEはコンピュータがたたき出した天才的なツールみたいな印象があるのか、「何でもCAEでやる」みたいな人もたまにいます。

手計算による理論と、CAEがどうやって結果を出したかというプロセスは実はほぼ同じなのです。

CAEは神様出なければなんなのか？

と、ここでCAEでそもそも一体何を見ているのかというのを考えてみましょう(^^)/

実現象をCAE解析で再現するまで

なぜかCAEというツールが先に存在しているようにCAE解析の経験から感じます。

CAEを使うことが大前提になっていますが、実は考え方は逆なのです。

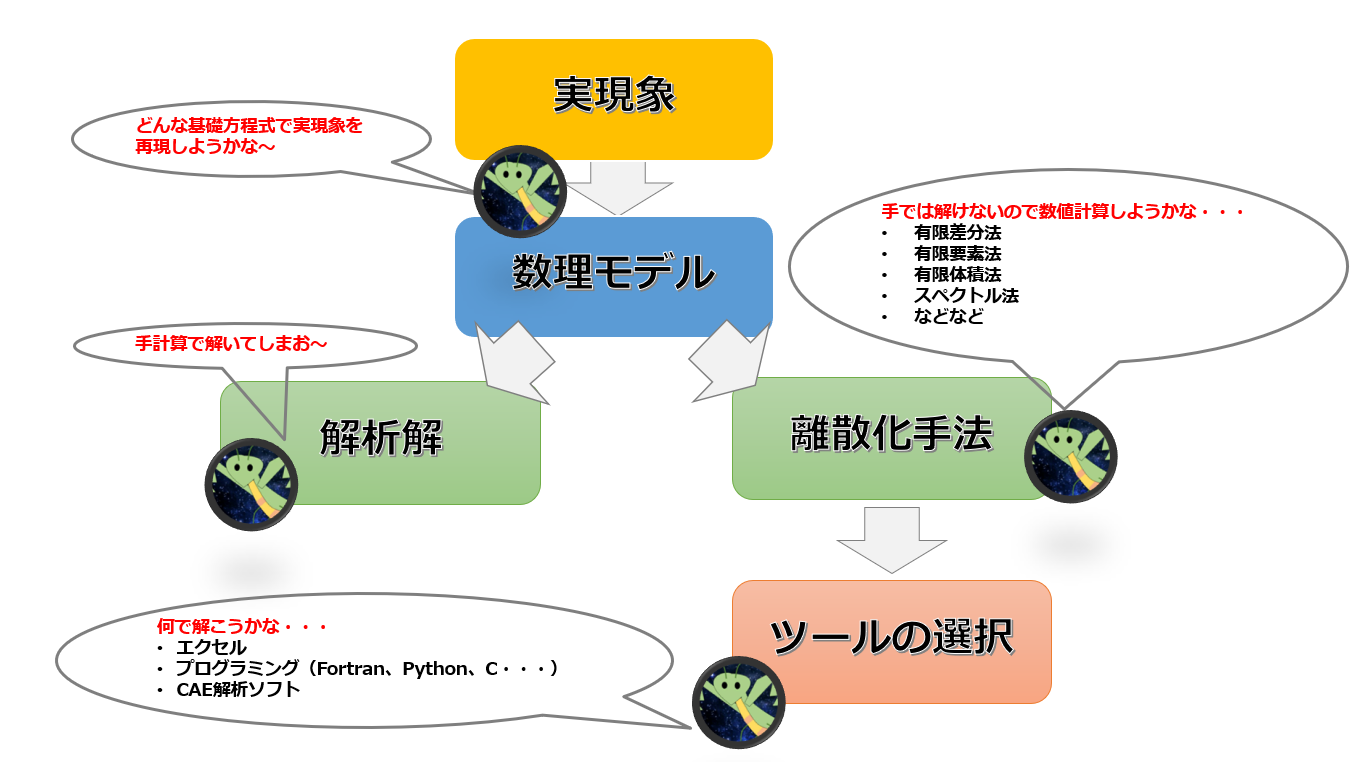
【実現象からCAE解析までのモデル化】

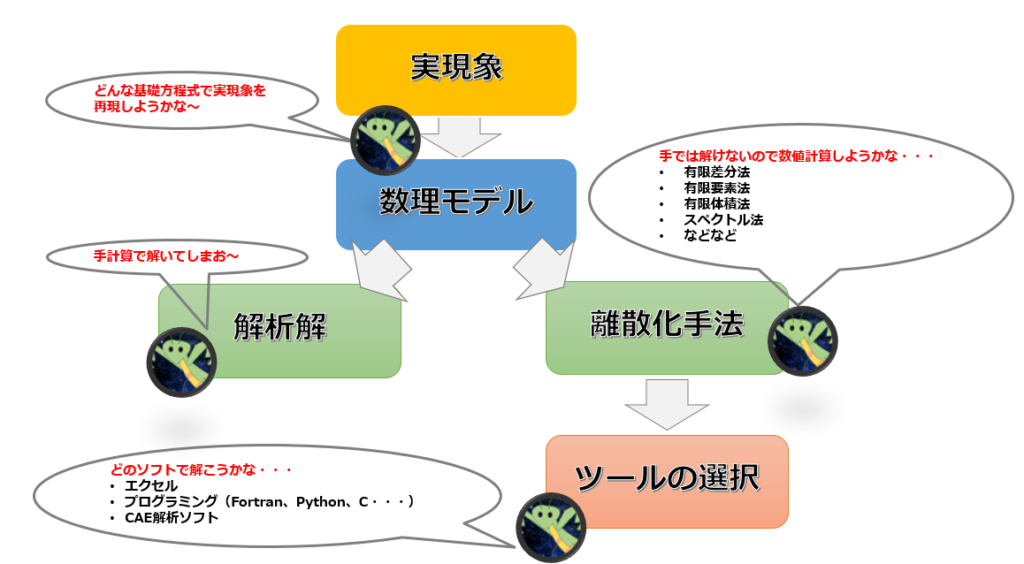
何が逆なのか？

CAEは初期条件を与えれば、決められた手続きに応じて勝手に答えを出してくれます。

CAEを使うなと言ってるのではなくて、

実現象から考えてツールを使うという思考をしなくては、とんでもない結果になりますよという注意喚起なのです！

見たい実現象に対する数理モデル

まず、見たい実現象に対してどんな数理モデルで再現しようかというのを考えます。

理想気体ではなく、分子間の相互作用を考慮した「ファンデルワールスの状態方程式」が実現象を再現するのに良いモデルだと思ったらそちらを使うでしょう。

別の例では、熱の伝達だから熱伝導方程式で良いなど・・・・・どのような方程式で実現象を扱うかがまずあるのです。

ここで実機の再現性の良しあしを決めるファーストステップに立っていることに気付くのです。

だから、実はCAEの精度云々は「数理モデル」の選択肢があっているかどうかからが問われます。

数理モデルを解ける形にする

次のステップはその方程式を解くという行為です。

そこで、与えられた方程式に対して手計算で解けるレベルであれば、手計算で解析解というのを解けば良いのです。

例え、難しい数式であったとしても手計算で解ける方程式であれば、そこから得られた解析解が何より最も精度の高い答えです。

何でもCAE頼みをしようとするのは、次の問題をわざわざコンピューターを使うのかという質問と同じです。

このように、数理モデルを仮定したら、まずその方程式の解析解（手計算での解）が求まるかどうかを考えるべきです。

手計算で解けないのであれば、方程式を離散化して数値解析を行うことになります。

ほとんどの物理現象の方程式は偏微分方程式なので直接解析解を出せるケースは少ないので、方程式を離散化して解くというのはよくあることです。

あるいは、形状自体が複雑（色んなところにRがあるなど）なので手計算では限界があるなども数値計算をする方向になります。

しかし、またここで離散化するがために精度は落ちます。

見たい現象に対して、偏微分であるものを代数のように解くわけですから、思いもよらない発散や数値的な不安定な事象が発生する場合があります。

手計算で解けない偏微分方程式はコンピューターに任せる

簡単なものであれば、エクセルやプログラミング言語などを駆使して自分で作って計算する方が良いでしょう。

理由は、自分で作ったプログラムはコードがわかるのでどのような計算をしているかが明確になります。

コードが用意されたソフトを使うのも手←ここでCAEソフトの出番！

もし、自分が見たい現象について既に専用のプログラムが組み込まれているCAE解析ソフトがあるのであれば、それを使用するのが良いでしょう。

実績と経験、場数を踏んだ商用のソフトであれば色々なエラーに対しても強いと思われます。

「実現象→数理モデル→偏微分方程式を解く→ツールを選択」という過程を経てCAEを使うことになります。

こういう風に全体を見渡すと、精度というのはどういう意味で使っているのかというのをもっと深く考えなくてはいけないことになります。

例えば、ファーストステップの「実現象と数値モデルのずれ」が精度と関係しているのであれば、実機の計測結果が実現象をちゃんと計測しているのかという問題もあります。

精度を求めて・・・・・行きつく先は一体どこなのでしょう？

まさか実機の代替えとしてCAEを使うってことを目的にCAEを使い始めたりするのでしょうか。

そうではないはずです。
元々物理の理論も「ある初期条件・環境からある時刻での物理量の変化や状態を予測する」ことに意味があるのです。

だとすればCAEは実機の代替えではなく、「この条件であればこういった傾向があることが予測される」という使い方をするべきだと考えられます。”この条件”というところにCAEの精度問題も含んでいますが、「こういう条件のもとであれば、こういった傾向があります」という結果は、十分使い道があるのです。

CAEは設計変数に対して見たい結果の挙動がどのように変わるのかという傾向分析の理解には繋がります。

結局CAEを使う目的とは？

だと考えています。

だから「1D CAE」などのような実現象の本質に立ち返った考え方ができてきているのです。

もちろんCAEと実機でのずれが生じた場合に、「なぜ理論ではこうなるはずなのに、実機での結果は違うのか」という視点から実機の計測方法の見直しなど、互いにフィードバックし合う関係であることは間違いありません。

一生懸命に精度を追い求めて、そしてCAEでたたき出した最適解を知りたいなどということよりも、

傾向の分析と最適解だと考えられる理由を考えるのに使うのがCAEなのではないかと考えています。

物理量の変化や状態を予測できた先もまた別の目的がある

物理量の変化や状態を予測できた♪ばんざい(‘ω’)ノ

ではないはずですよね。

それを設計・開発に結び付けれるかどうかが当然試されます。

つまり・・・