こんにちは(@t_kun_kamakiri)(^^)/
台所でふとこのように思ったことはありませんかね？
今日は、家庭でも役に立つお話をしたいと思います。ちなみに先日に☟こういったツイートをしてアンケートを取ってみました。
「凍ったビールが入った缶」
と
「凍ってないビールが入った缶」
を斜面を転がすとどちらが斜面を下るのが速いか？
※どちらも滑らず転がる— カマキリ🐲@ブログとnote書いている (@t_kun_kamakiri) July 3, 2020
どういう内容かと言いますと・・・
【問題１】
「凍ったビールが入った缶」と「凍っていないビールが入った缶」を同じ高さから斜面を転がします。
どちらがはやく斜面を下るでしょうか？
【問題２】
「ゆで卵」と「生卵」を同じ高さから斜面を転がします。
どちらがはやく斜面を下るでしょうか？
ここで上の2問のポイントをまとめておきましょう。
絵にすると☟こちら！！
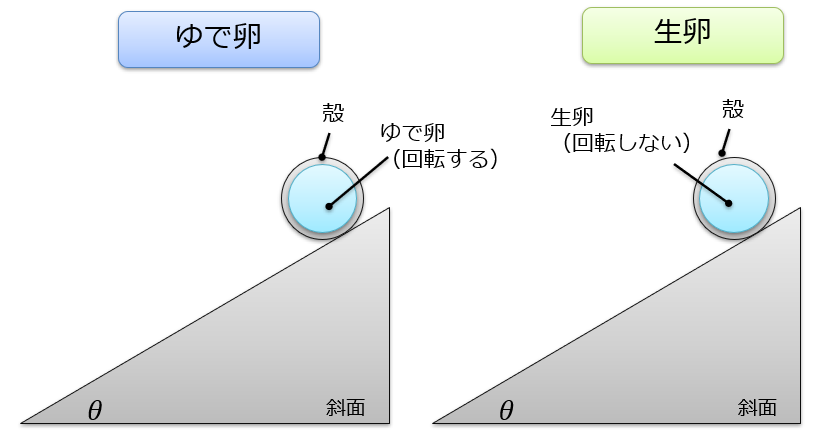
簡単に言うと、「中身が回転する」場合と「中身が回転しない場合」ではどちらが斜面をはやく下るでしょうか？という問題になります。
なんだって！！？
って思った人も多いかと思います。
これは少々意外な答えであるようにも感じますよね。
実際に友達にも質問すると・・・
こういった印象で答えてくれます！
が、質量が大きいものと小さいもので落下速度は質量が大きいもの方が速いように思えますが、実際には違いがないことは有名な話ですよね。（大きさもなく、空気抵抗などは考えないとして）
このように、印象だけで答えるとやはり実現象はどうなっているのかわからないので、本記事では力学的な観点から「なぜ、ゆで卵と生卵では生卵の方が斜面を下るのがはやいのか」といったことが起こるのかを解説します。
「なぜ、ゆで卵と生卵では生卵の方が斜面を下るのがはやいのか」といったことが起こるのかを解説
- 運動方程式から考える
- エネルギー保存則から考える
運動方程式から考える
まず、現象を理解するためには現象をモデル化する必要があります。
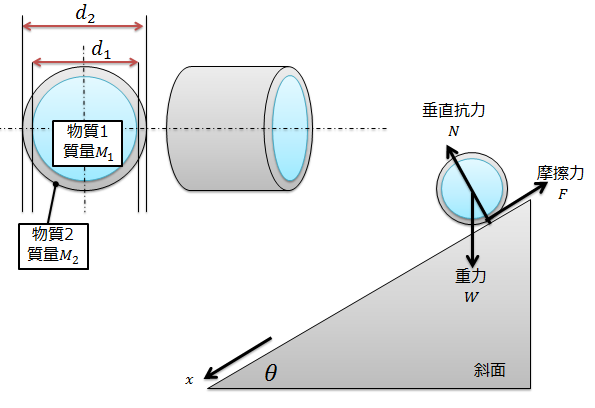
今回は、シンプルなモデルで考えたいので以下のような状況下で考えてみることにします。
- 空気抵抗なし
- 奥行方向は一様
- 中身と外側の間には摩擦力は無し
回転運動を考えるには、物体の慣性モーメントを考える必要があります。
慣性モーメントとは「回転のしにくさ」を表わす量です。
（質量\(m\)が「加速のしにくさ」を表わす量であるように・・・）
中身が回転する場合を考えて、中身が回転しない場合は中身の慣性モーメントをゼロにする
- \(d_{1}=2r_{1}\)
- \(d_{2}=2r_{2}\)
このように考えたときの、「物質1」と「物質2」の慣性モーメントがどうなっているのかを計算しておくと後々便利です。
- 物質1の慣性モーメント：\(I_{1}=\frac{1}{2}M_{1}r_{1}^{2}\)
- 物質2の慣性モーメント：\(I_{2}=\frac{1}{2}M_{2}\big(r_{1}^{2}+r_{2}^{2}\big)\)
では、「運動方程式」と「回転の運動方程式」と「速度と角速度」を立式して並進運動の加速度を求めていきましょう(^^)/
運動方程式
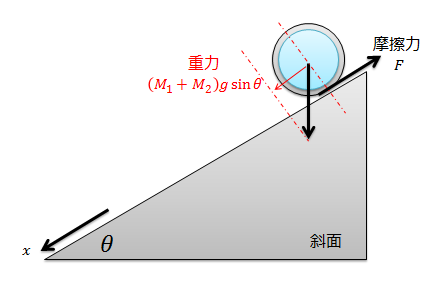
並進方向（\(x\)方向）の運動方程式を考えます。
(M_{1}+M_{2})\frac{d^2x}{dt^2}=(M_1+M_2)g\sin\theta-F\tag{1}
\end{align*}
回転の運動方程式
回転運動は摩擦力\(F\)によって生じます。
I\frac{d^2\varphi}{dt^2}=Fr_{1}\tag{2}
\end{align*}
※慣性モーメントは\(I=I_{1}+I_{2}\)
速度と角速度の関係
回転する円においては、並進運動で移動した距離\(x\)と回転角との間には関係性があります。
x=r_{1}\varphi\tag{3}
\end{align*}
これを\(t\)で2階微分すると、
\frac{d^2x}{dt^2}=r_{1}\frac{d^2\varphi}{dt^2}\tag{3.1}
\end{align*}
これで運動方程式が立てれました。
今求めたいのは、並進運動の加速度ですので(1)(2)(3.1)から、摩擦力\(F\)を消去して整理します。
すると、
\frac{d^2x}{dt^2}=\frac{(M_{1}+M_{2})r_{1}^2}{\left\{(M_{1}+M_{2})^2+I\right\}}g\sin\theta\tag{4}
\end{align*}
これらの結果をまとめると以下のようになります。
慣性モーメント\(I\)は回転のしにくさの量、質量\(M\)は加速のしにくさを表す量なのですが、
もう少し直感的な説明ができても良いのではないかと思っています。
エネルギーの保存則から直感的に考える
今度はエネルギー保存則の観点から考えてみましょう。
こちらの説明の方が直感的で理解がしやすいかと思います。
「ゆで卵」も｢生卵｣も同じ高さから転がすのであれば位置エネルギーが同じということになります。
慣性モーメント\(I\)は回転エネルギーを担っている量に関係していて、質量\(M\)は並進運動エネルギーを担っている量とも言えます。
そうすると、斜面を下っている間は、エネルギーの保存則より、もともと持っていた位置エネルギーは「並進運動のエネルギー」と「回転の運動エネルギー」に分配されて時間が進むという事になります。
つまり、式で書くと以下となります。
Mgh=\frac{M}{2}v_{G}^{2}+\frac{I}{2}\omega^{2}\tag{4}
\end{align*}
となります。
※\(M=M_{1}+M_{2}\)
※\(\frac{d\varphi}{dt}=\omega\)：角速度
今回は、重心位置が円の中心に来ているのでとても簡単ですね。
式で書くとごちゃごちゃしていますが、要するに↓こういうことです。
繰り返しになりますが、斜面を下っている間は、エネルギーの保存則より、もともと持っていた位置エネルギーは「並進運動のエネルギー」と「回転の運動エネルギー」に分配されて時間が進むという事になります。
だから、ゆで卵の場合は中身も回転してしまい、エネルギーの多くが回転運動に使われてしまっているので、生卵と比べて斜面を下るのが遅いという結論になります。
↑こういった感じです。
まとめ
「中身が回転する」場合と「中身が回転しない場合」ではどちらが斜面をはやく下るでしょうか？という問題に対して、
というのを力学的な観点から説明をしました(^^)/
なので、ゆで卵か生卵かわからなくなったときは、斜面をコロコロ転がすか、その場で卵を回してみてください！
斜面を早く下る方が生卵ですし、その場で回してみてあまり回らない方が生卵です！
実際に、どうなのかはご家庭で試してみると良いでしょう。
今回の内容から得た教訓は、
- 何事も理論から考えてみるというのはとても大事
- 人は直感で生きている
- でも、直感の方が当たっている場合も多い
- 理論だけに頼らず実験でも試してみることはとても大事
「直感に頼り、理論で確信を得て、実験で試す」という行程はとても大事なのではないかと感じます。
もっと力学について勉強したいという方のために、入門から中級レベルまでの参考書を紹介しておきます。
↓こちらの参考書は問題集ですが、大学で勉強するだいたいの問題は載っています。
なので、大学院入試やレポート課題の際にはとても役に立つ1冊です。
※ただし、辞書的な使い方をする方が良く、「全部解いてやるぞー」って意気込むものではありません。
Follow @t_kun_kamakiri 