こんにちは(@t_kun_kamakiri)(^^)/
今回はN重振り子の運動方程式の問題を取り扱います。
N重振り子の運動方程式を導く。
- N重振り子の運動
- ラグランジュ方程式から運動方程式を導く
- N重振り子の数値計算
こちらの記事を読んで
振り子の運動を数値計算で再現したい方には参考になる記事です。
N重振り子の運動方程式
本記事では一般的なN重振り子の問題を考えますが、慣れない方は2重振り子や3重振り子など自由度の少ないの運動方程式から考えてみても良いでしょう。
一般的には自由度が大きくなるとそれだけ問題が複雑になるのですが、逆に自由度が多いほうが帰って式がシンプルになる場合があります。
なので、今回はあえてN個の質点が連なった振り子の問題を扱おうと思います。
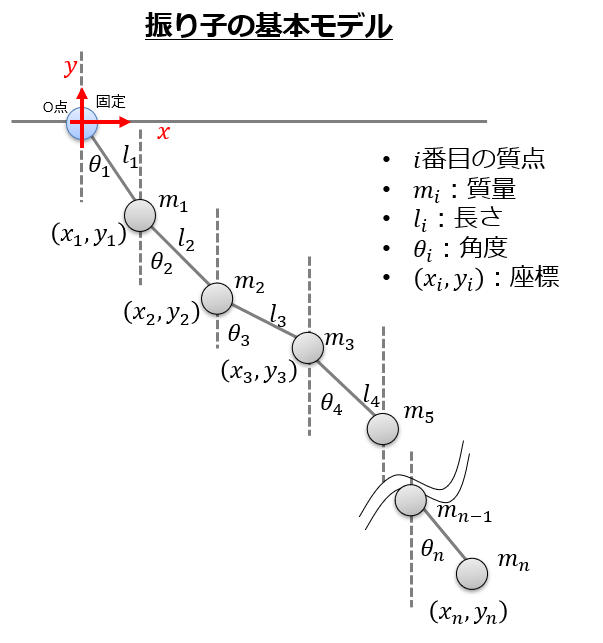
- 質点の質量:$m_{i}$
- 質点の位置:$(x_{i},y_{i})$
- 質点間の長さ:$l_{i}$
質点には重力加速度$m_{i}g$がはたらいています。

運動方程式と等価な方程式
力学の問題を解く際には、まず運動方程式である偏微分方程式を導出する必要があります。
運動方程式と等価となる方程式はいくつか方法かあって、問題に応じて適した方法を用いれば良いと思います。
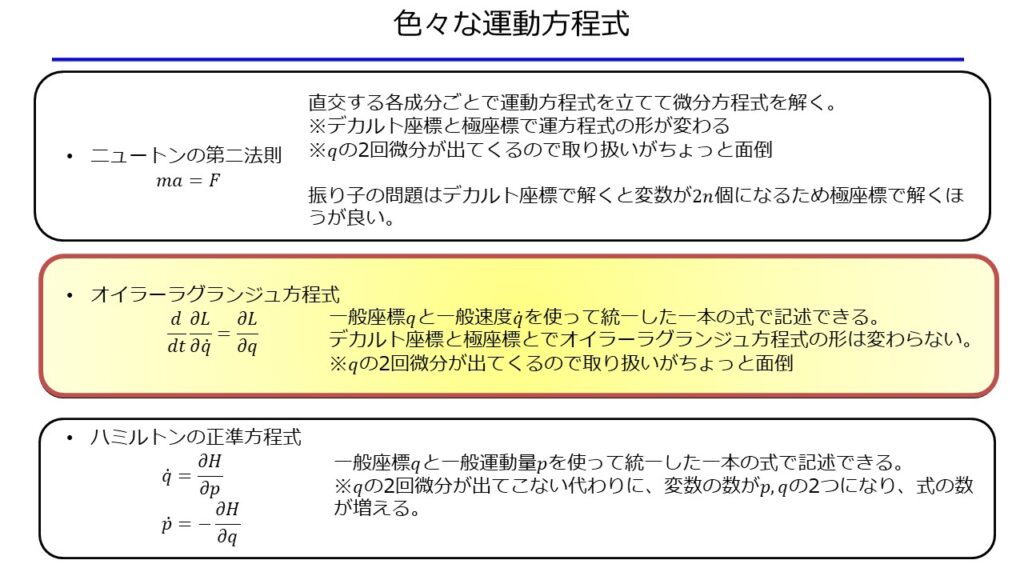
代表的な運動方程式と等価な方程式を示します。
このどれを使っても良いのですが、今回は簡単に運動方程式を導くことができるオイラー・ラグランジュ方程式を使った運動方程式の導出方法を紹介します。
運動方程式を導く
運動方程式を導くを導くまでのフローを以下に記します。
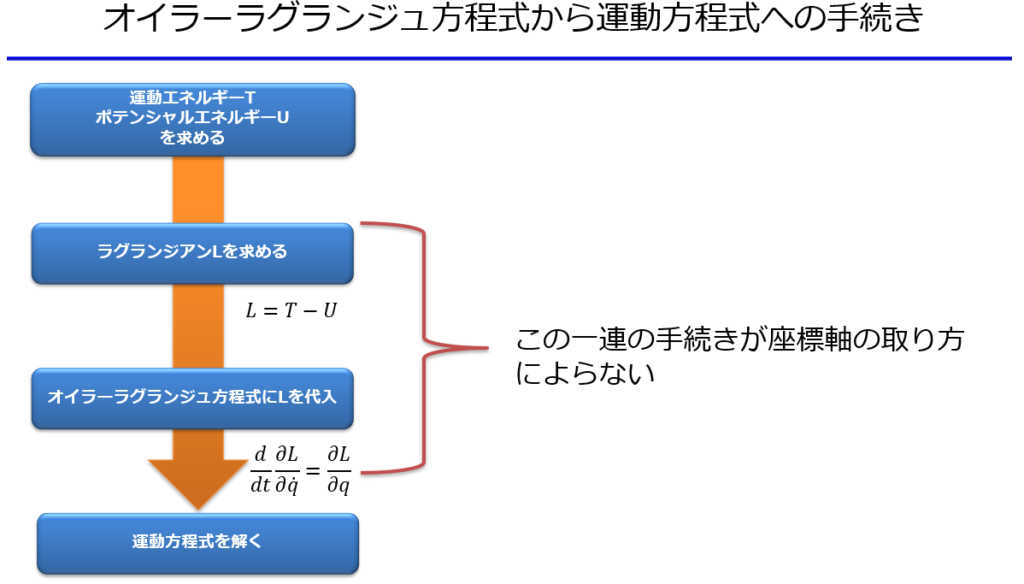
x_{i}&=\sum_{j=1}l_{j}\sin\theta_{j}\tag{1}\\
y_{i}&=\sum_{j=1}-l_{j}\cos\theta_{j}\tag{2}
\end{align*}
まずは運動方程式を書き下します。
T&=\sum_{i=1}^{n}\frac{1}{2}m_{i}(\dot{x}_{i}^2+\dot{y}_{i}^2)\\
&=\sum_{j=1}^{n}\sum_{k=1}^{i}l_{j}l_{k}\dot{\theta}_{j}\dot{\theta}_{k}\cos(\theta_{j}-\theta_{k})\tag{3}
\end{align*}
次に位置エネルギーを書きます。
U&=\sum_{i=1}^{n}mgy_{i}\\
&=\sum_{i=1}^{n}mg\sum_{j=1}^{i}-l_{i}\cos\theta_{i}\tag{4}
\end{align*}
ここでの変数は$x_{i},y_{i}$ではなく、$l_{i},\theta_{i}$が、$l_{i}$は固定値なので実際取り扱う変数は$\theta_{i}$のみです。
そして、$N$個の質点があるので自由度は$N$ということになりますね。
ラグランジアンを求める
運動方程式を導くには、ラグランジアン$L=T-U$を求めてオイラー・ラグランジュ方程式に代入すれば良いので、まずはラグランジアンを求めます。
ラグランジュ方程式の導出の仕方は↓こちらの記事に書いていますのでご参考ください。
L&=T-U\\
&=\sum_{j=1}^{n}\sum_{k=1}^{i}l_{j}l_{k}\dot{\theta}_{j}\dot{\theta}_{k}\cos(\theta_{j}-\theta_{k})+\sum_{i=1}^{n}mg\sum_{j=1}^{i}l_{i}\cos\theta_{i}\tag{5}
\end{align*}
ここでの一般化座標は$\theta$だし、一般化速度は$\dot{\theta}$であることに注意して、次はオイラー・ラグランジュ方程式から運動方程式を導く計算を進めていきます。
オイラー・ラグランジュ方程式から運動方程式を導く
オイラー・ラグランジュ方程式は以下で与えられます。
\frac{d}{dt}\frac{\partial L}{\partial \dot{q}}=\frac{\partial L}{\partial q}\tag{6}
\end{align*}
(6)に(5)を代入します。
l_{i}\sum_{j=1}^{n}\bigg(\sum_{k=max(i,j)}^{n}m_{k}\bigg)l_{j}\left \{ \ddot{\theta_{j}}\cos(\theta_{i}-\theta_{j}) -\dot{\theta}_{j}\big(\theta_{i}-\theta_{j}\big)\sin(\theta_{i}-\theta_{j})\right \}\\
=-l_{i}\left \{\sum_{j=1}^{n}\bigg(\sum_{k=max(i,j)}^{n}m_{k}\bigg)\big(l_{j}\dot{\theta}_{i}\dot{\theta}_{j}\sin(\theta_{i}-\theta_{j})\big) +\big(\sum_{k=i}^{n}g\sin\theta_{i}\big) \right \}\tag{7}
\end{align*}
今回の運動方程式(偏微分方程式)における変数は$\theta$なので、$\theta$に関する2階微分方程式であることに注意します。
ここで、自由度が$N$個あるので方程式を整理すると$N$行$N$列の行列Aと$B$を使って整理することができます。
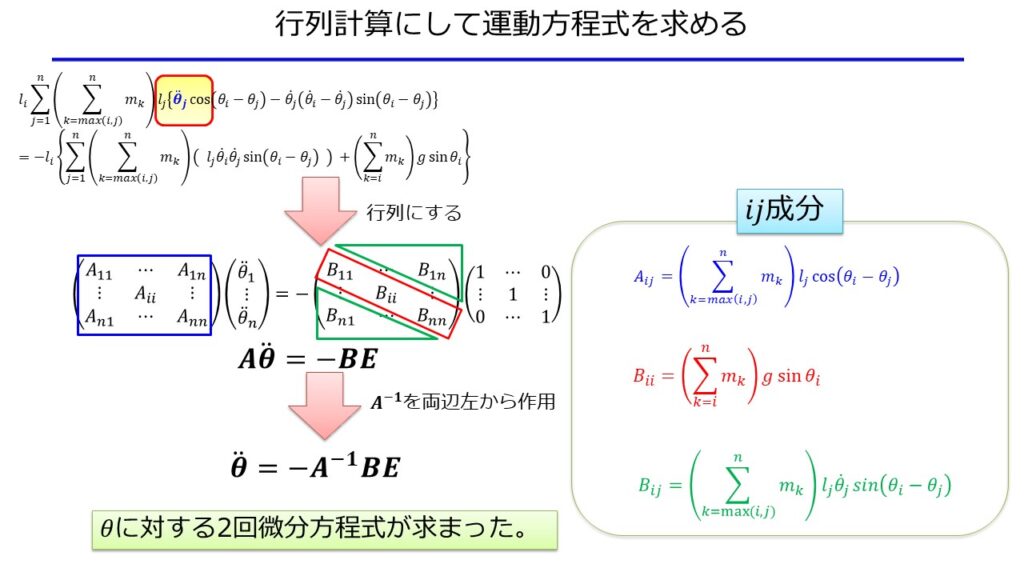
行列計算を解くだけということになります。
\ddot{\theta}=-A^{-1}BE\tag{8}
\end{align*}
行列$B$については、対角成分と非対角成分とで式の形が異なるので注意が必要です。
$N$重振り子の場合の運動方程式が(8)の形で書け、行列計算を行えば時刻$t$での$\theta(t)_{1},\theta(t)_{2},\cdots ,\theta(t)_{n}$がわかるということですね。
計算の途中で、逆行列$A^{-1}$を計算する必要がありますが、プログラミング言語Pythonの数値計算用のライブラリであるnumpyを使えば簡単に計算ができます。
PythonでN重振り子の運動の数値計算
Pythonを使って(8)の数値計算をしたいと思います。
今回は、以下のようにExcelに振り子のパラメータになる重量と質点間距離を書き込んでおき、PythonからExcelデータを読み込むプログラムにしたいと思います。
その方が、もしPythonを知らない人でもExcel内のパラメータを変えることで計算ができるようになるからです。
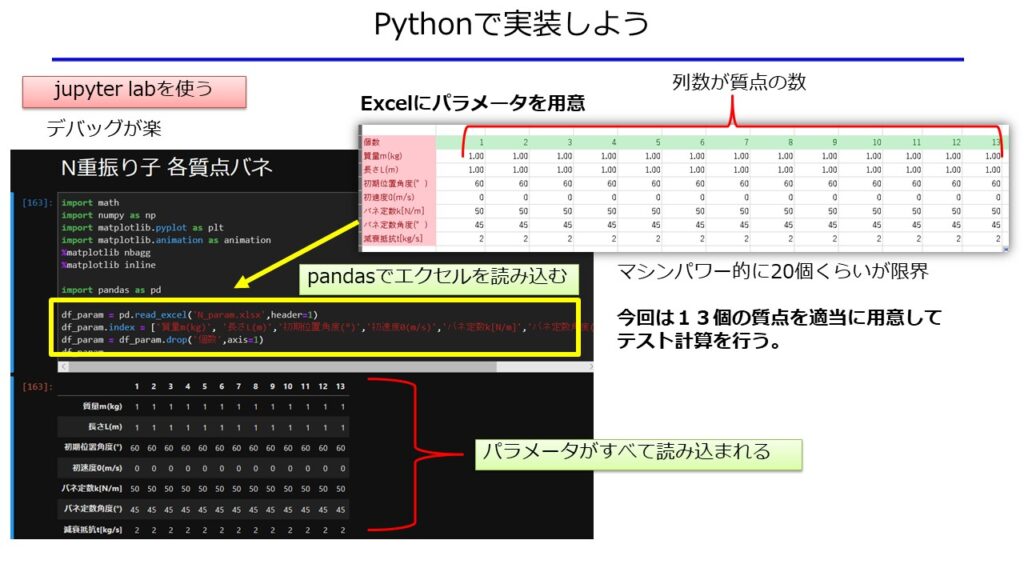
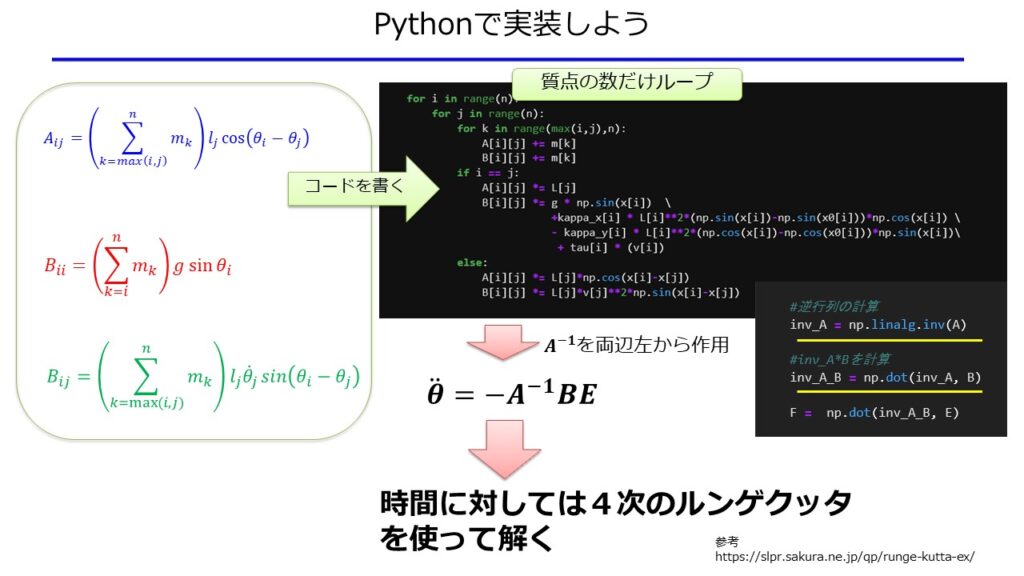
解くべき方程式である(8)$\ddot{\theta}=-A^{-1}BE$は$\theta$に関する2階微分方程式であるため、時間の積分を数値的に行う必要があります。
時間の数値積分は精度の良い4次のツンゲクッタを使って解くことにします。
jupyter labを使ってプログラムを作成します。
pandasからExcelを読み込む部分で XLRDError: Excel xlsx file; not supported というエラーになってしまいます。理由は、pd.read_excel() のデフォルトエンジンが xlrd のためでです。対策は pip install openpyxl で openpyxl をインストールしてpd.read_excel('N_param0.xlsx',header=1, engine='openpyxl')と書けば良いです。
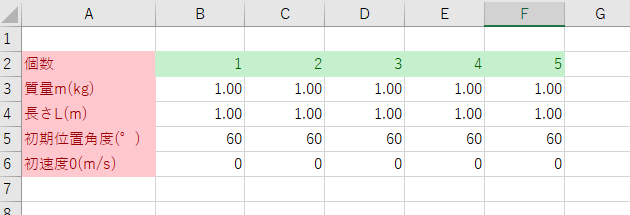
まずはExcelを用意します。
質点の数は何個でも良いのですが、今回は5個にしておきます。
質点の数を増やしたい場合はG列以降にも値を書き込んでいけば自動的に質点の数が増えて振り子の計算してくれます。
必要なライブラリをインポートします。
|
1 2 3 4 5 6 7 |
#from numpy import sin, cos import math import numpy as np import matplotlib.pyplot as plt import scipy.integrate as integrate import matplotlib.animation as animation import pandas as pd |
次にExcelのデータをpandasで読み込みます。
|
1 2 3 4 |
df_param = pd.read_excel('N_param0.xlsx',header=1, engine='openpyxl') df_param.index = ['質量m(kg)', '長さL(m)','初期位置角度(°)','初速度0(m/s)'] df_param = df_param.drop('個数',axis=1) df_param |
ちゃんと読み込めているか確認しましょう。
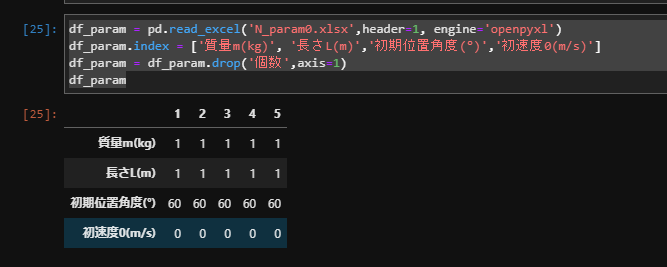
値が正しく読み取れているか確認しておきます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
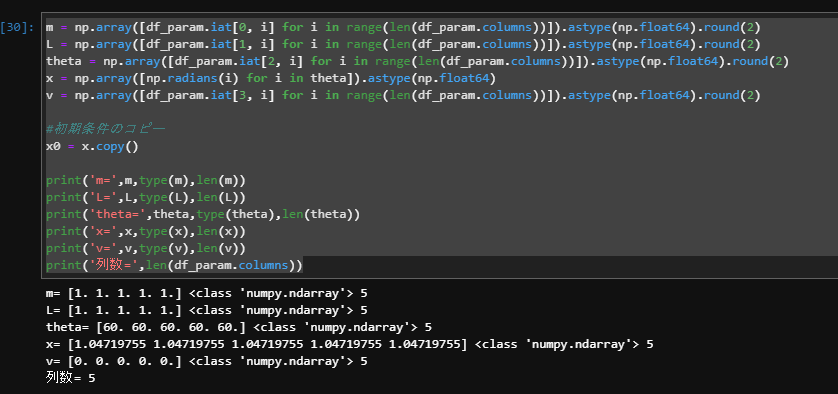
m = np.array([df_param.iat[0, i] for i in range(len(df_param.columns))]).astype(np.float64).round(2) L = np.array([df_param.iat[1, i] for i in range(len(df_param.columns))]).astype(np.float64).round(2) theta = np.array([df_param.iat[2, i] for i in range(len(df_param.columns))]).astype(np.float64).round(2) x = np.array([np.radians(i) for i in theta]).astype(np.float64) v = np.array([df_param.iat[3, i] for i in range(len(df_param.columns))]).astype(np.float64).round(2) #初期条件のコピー x0 = x.copy() print('m=',m,type(m),len(m)) print('L=',L,type(L),len(L)) print('theta=',theta,type(theta),len(theta)) print('x=',x,type(x),len(x)) print('v=',v,type(v),len(v)) print('列数=',len(df_param.columns)) |
良さそうだったら、振り子の初期状態を確認しましょう。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
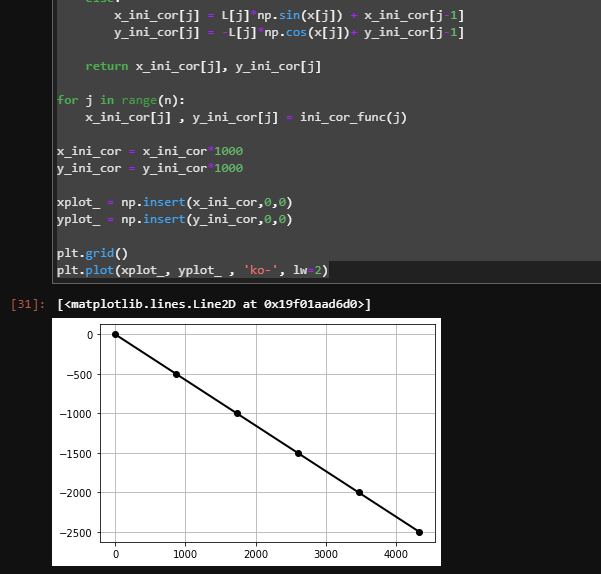
#初期位置の確認 n = len(df_param.columns) x_ini_cor = np.zeros(n,dtype=np.float64) y_ini_cor = np.zeros(n,dtype=np.float64) def ini_cor_func(j): if j == 0: x_ini_cor[j] = L[j]*np.sin(x[j]) y_ini_cor[j] = -L[j]*np.cos(x[j]) else: x_ini_cor[j] = L[j]*np.sin(x[j]) + x_ini_cor[j-1] y_ini_cor[j] = -L[j]*np.cos(x[j])+ y_ini_cor[j-1] return x_ini_cor[j], y_ini_cor[j] for j in range(n): x_ini_cor[j] , y_ini_cor[j] = ini_cor_func(j) x_ini_cor = x_ini_cor*1000 y_ini_cor = y_ini_cor*1000 xplot_ = np.insert(x_ini_cor,0,0) yplot_ = np.insert(y_ini_cor,0,0) plt.grid() plt.plot(xplot_, yplot_ , 'ko-', lw=2) |
微分方程式を解くプログラムを作成します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 |
#Calculate propertv init = 0 end = 10 dt = 0.05 h = dt loop = int(end/h) n = len(df_param.columns) g = 9.8 # initial state t = init tpoints = np.arange(init, end , h) xpoints = [] vpoints = [] # A = np.zeros((n,n),dtype=np.float64) # B = np.zeros((n,n),dtype=np.float64) E = -np.ones_like(x) def N_func(t, x, v): A = np.zeros((n,n),dtype=np.float64) B = np.zeros((n,n),dtype=np.float64) for i in range(n): for j in range(n): for k in range(max(i,j),n): A[i][j] += m[k] B[i][j] += m[k] if i == j: A[i][j] *= L[j] B[i][j] *= g * np.sin(x[i]) else: A[i][j] *= L[j]*np.cos(x[i]-x[j]) B[i][j] *= L[j]*v[j]**2*np.sin(x[i]-x[j]) #逆行列の計算 inv_A = np.linalg.inv(A) #inv_A*Bを計算 inv_A_B = np.dot(inv_A, B) F = np.dot(inv_A_B, E) return F xpoints = [] vpoints = [] #配列要素数の定義 j1 = np.zeros_like(v) k1 = np.zeros_like(x) j2 = np.zeros_like(v) k2 = np.zeros_like(x) j3 = np.zeros_like(v) k3 = np.zeros_like(x) j4 = np.zeros_like(v) k4 = np.zeros_like(x) def RK(t,x,v): vt = v.copy() xt = x.copy() xpoints.append(xt) vpoints.append(vt) j1 = N_func(t, x, v) * h k1 = v * h j2 = N_func(t + h / 2, x + k1 / 2, v + j1 / 2) * h k2 = (v + j1/ 2)* h j3 = N_func(t + h / 2, x + k2 / 2, v + j2 / 2) * h k3 = (v + j2/ 2)* h j4 = N_func(t + h, x + k3, v + j3)*h k4 = (v + j3)* h v += (j1 + 2*j2 + 2*j3 + j4)/6 x += (k1 + 2*k2 + 2*k3 + k4)/6 return x,v,xpoints ,vpoints |
後は、時間に対してどんどん積分を繰り返します。
|
1 2 3 4 5 6 7 8 |
# from ipykernel import kernelapp as app for t in range(len(tpoints)): # for t in range(2): x, v, xpoints, vpoints= RK(t,x,v) xpoints = np.array(xpoints) vpoints = np.array(vpoints) |
ここまでで$\theta(t)_{1},\theta(t)_{2},\cdots,\theta(t)_{5}$が求まりましたが、振り子のアニメーションを作成するために、$x(t),y(t)$に変換する必要があります。
|
1 2 3 4 5 |
xt = np.zeros(len(xpoints)) def xt_func(j): xt = xpoints[:,j] return xt |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
x_cor = np.zeros((len(xpoints),n),dtype=np.float64) y_cor = np.zeros((len(xpoints),n),dtype=np.float64) def cor_func(j): if j == 0: x_cor[:,j] = L[j]*np.sin(xt_func(j)) y_cor[:,j] = -L[j]*np.cos(xt_func(j)) else: x_cor[:,j] = L[j]*np.sin(xt_func(j)) + x_cor[:,j-1] y_cor[:,j] = -L[j]*np.cos(xt_func(j))+ y_cor[:,j-1] return x_cor[:,j], y_cor[:,j] for j in range(n): x_cor[:,j] , y_cor[:,j] = cor_func(j) x_cor = x_cor*1000 y_cor = y_cor*1000 |
アニメーションにする前にどういった挙動をしているのかをグラフにしてみます。
|
1 2 |
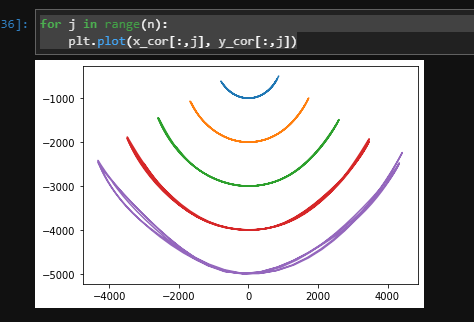
for j in range(n): plt.plot(x_cor[:,j], y_cor[:,j]) |
正しそうな挙動をしていますね。
では、アニメーションを作成します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
fig = plt.figure() ax = fig.add_subplot(111, autoscale_on=False, xlim=(-n*1000, n*1000), ylim=(-n*1000-n*1000*0.5, n*1000-n*1000*0.5) ) #xlim=(-n*1000, n*1000), ylim=(-n*1000-n*1000*0.5, n*1000-n*1000*0.5) ax.grid() line, = ax.plot([], [], 'o-', lw=2) time_template = 'time = %.1fs' time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes) def init(): line.set_data([], []) time_text.set_text('') return line, time_text def animate(i): thisx = [] thisy = [] thisx.append(0) thisy.append(0) for j in range(n): thisx.append(x_cor[i,j]) thisy.append(y_cor[i,j]) line.set_data(thisx, thisy) time_text.set_text(time_template % (i*dt)) return line, time_text ani = animation.FuncAnimation(fig, animate, np.arange(1, len(tpoints)), interval=25, blit=True, init_func=init) # ani.save('N_furiko_spring.mp4', fps=15) writergif = animation.PillowWriter(fps=30) ani.save('N_furiko_spring.gif',writer=writergif) # plt.show() |
朝からこれ書いている。#Python pic.twitter.com/hSaDhvT6Xm
— カマキリ🐲Python頑張る昆虫 (@t_kun_kamakiri) May 1, 2021
うまくいったのではないでしょうか(^^♪
まとめ
N重振り子の運動方程式をオイラー・ラグランジュ方程式を使って導出し、Pythonで実装してアニメーションにしました。