こんにちは(@t_kun_kamakiri)(^^)/
前回では「逆行列の定義」についての内容をまとめました。
逆行列の定義だけではイメージがつかないと思い、3行3列の逆行列を余因子行列を用いて逆行列を計算する例題演習を用意しました。
3行3列の行列の逆行列の例題演習を行う。
- 逆行列とは何か?
- 逆行列が存在する条件
- 余因子行列から逆行列を計算する
「こちら行列$A$の逆行列を求めてみましょう」というのが本記事の内容です。
A=\begin{pmatrix}
3& -2& 5\\
1& 3& 2\\
2& -5&-1
\end{pmatrix}\tag{1}
\end{align*}
これから線形代数を学ぶ学生や社会人のために「役に立つ内容にしたい」という思いで記事を書いていこうと考えています。
- 行列をはじめて習う高校生・大学生
- 仕事で行列を使うけど忘れてしまった社会人
この記事の内容をマスターして行列計算を楽に計算できるようになりましょう(^^)
逆行列とは?逆行列存在する条件
逆行列はスカラー量における割り算に相当するものだと考えてください。
$n$次正方行列$A$に対して$XA=AX=E$($E$は単位行列)となる行列$X$が存在するとき、$X$を$A$の逆行列と言い、$X=A^{-1}$と表します。
※行列には割り算の記法がないため$\frac{1}{A}$とは書きません。
余因子行列$\tilde{A}$は逆行列を計算する際に必要ですのでおさえておきましょう!
\tilde{A}=\underset{転置行列であることに注意}{{}^t\!\begin{pmatrix}
\tilde{a}_{11} &\tilde{a}_{12} &\cdots &\tilde{a}_{1n} \\
\tilde{a}_{21} &\tilde{a}_{22} &\cdots &\tilde{a}_{2n} \\
\cdots &\cdots&\cdots &\cdots \\
\tilde{a}_{n1} &\tilde{a}_{n2} &\cdots &\tilde{a}_{nn} \\
\end{pmatrix}}\\
=\begin{pmatrix}
\tilde{a}_{11} &\tilde{a}_{21} &\cdots &\tilde{a}_{n1} \\
\tilde{a}_{12} &\tilde{a}_{22} &\cdots &\tilde{a}_{n2} \\
\cdots &\cdots&\cdots &\cdots \\
\tilde{a}_{1n} &\tilde{a}_{2n} &\cdots &\tilde{a}_{nn} \\
\end{pmatrix}
\end{align*}
逆行列$A^{-1}$は、
と書けます。
逆行列が存在する条件
逆行列を求める際には、まず行列式を計算します。
なぜなら行列式の結果が0か0ではないかで逆行列が定義できるかどうかの判断材料になるからです。
\left\{\begin{matrix}
|A|\neq 0のとき& Aは正則\rightarrow 逆行列A^{-1}が存在する\\
|A|=0のとき & Aは正則ではない\rightarrow 逆行列A^{-1}が存在しない
\end{matrix}\right.
\end{align*}
さらに、行列式は任意の行列に対して存在するのではなく正方行列(行と列が同じ数の行列)のみ存在します。
以上の内容をまとめると逆行列が必要十分条件は、
【例題演習】3行3列の逆行列も求めてみよう
では、具体的な行列を使って逆行列を計算してみましょう。
ここでは以下の3行3列の正方行列Aの逆行列を余因子行列を使って計算してみましょう。
逆行列$A^{-1}$は、
まずは、逆行列が存在する条件を満たしているのかどうかを確認します。
逆行列が存在する条件を確認
逆行列が存在する条件は以下でしたね。
正方行列であるので行列式が計算できるので、まずは行列式を求めます。
3行3列の行列式はサラスの公式を使えば簡単に求まりますね(^^)
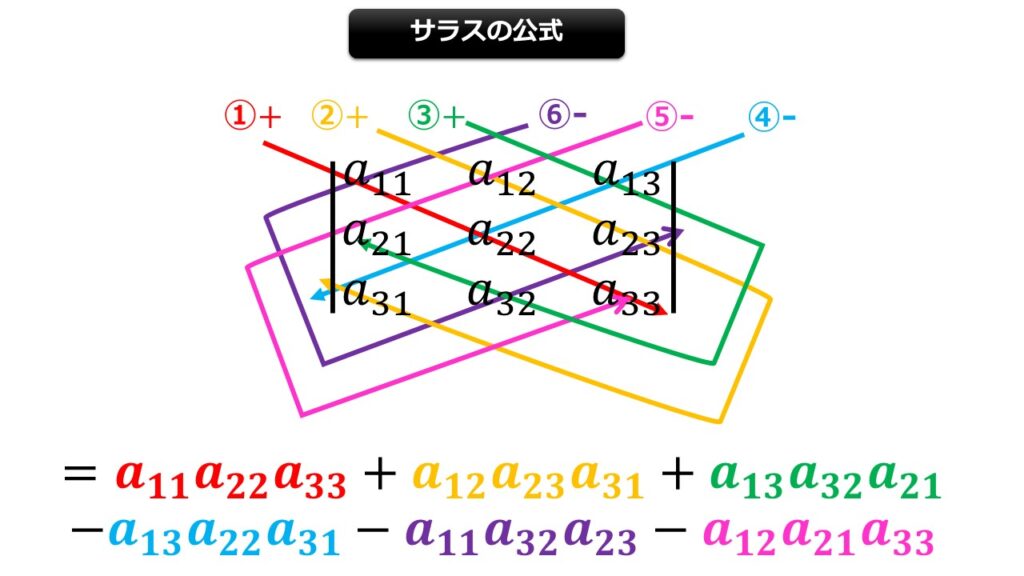

行列式$|A|$は、
|A|&=\begin{vmatrix}
3& -2& 5\\
1& 3& 2\\
2& -5&-1
\end{vmatrix}\\
&=3\times 3\times (-1)+(-2)\times 2 \times 2+5\times (-5)\times 1\\
&-\big(2\times 3\times 5 +(-2)\times 1\times (-1) + 3\times (-5)\times 2\big)\\
&=-44\tag{3}
\end{align*}
$|A|\neq 0$なので逆行列が存在することがわかりました。
余因子行列を求める
あとは余因子行列を計算すれば良いですね。
3行3列の余因子行列は以下となります。
\tilde{A}&=\underset{転置行列であることに注意}{{}^t\!\begin{pmatrix}
\tilde{a}_{11} &\tilde{a}_{12}&\tilde{a}_{13} \\
\tilde{a}_{21} &\tilde{a}_{22}&\tilde{a}_{23} \\
\tilde{a}_{31} &\tilde{a}_{32}&\tilde{a}_{33}
\end{pmatrix}}\\
&=\begin{pmatrix}
\tilde{a}_{11} &\tilde{a}_{21}&\tilde{a}_{31} \\
\tilde{a}_{12} &\tilde{a}_{22}&\tilde{a}_{32} \\
\tilde{a}_{13} &\tilde{a}_{23}&\tilde{a}_{33}
\end{pmatrix}
\end{align*}
行列要素の余因子$\tilde{a}_{ij}$を9個も計算しないといけないのでちょっと面倒ですが、余因子の計算方法さえ覚えていれば計算自体は簡単です。
例えば(1,2)成分の$\tilde{a}_{12}$の場合の場合は↓このようにして求めます。


では、9個の余因子を計算しましょう。
以下のように、不必要な行と列を隠しながら2行2列の行列式を計算していけば良いですね。
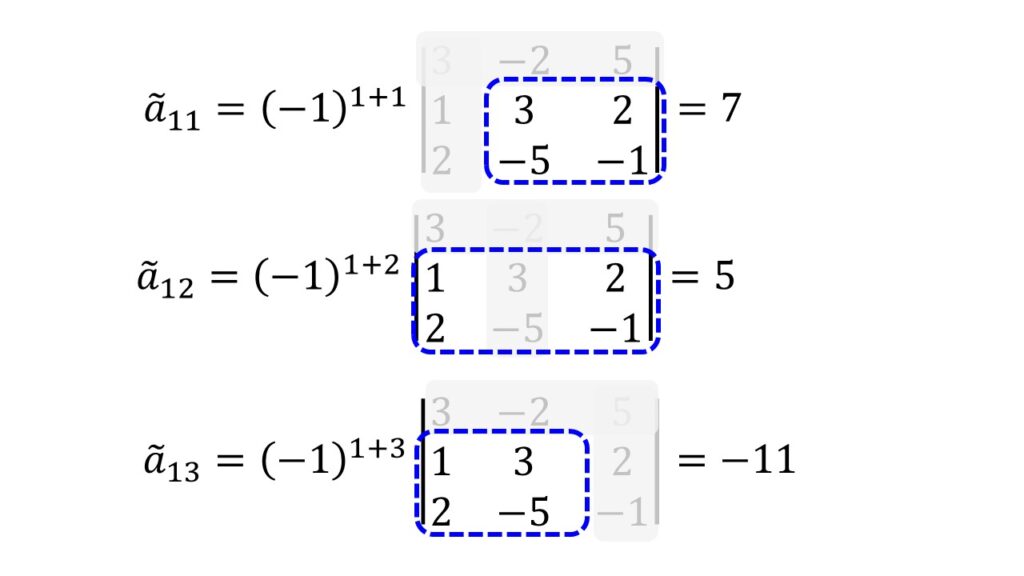

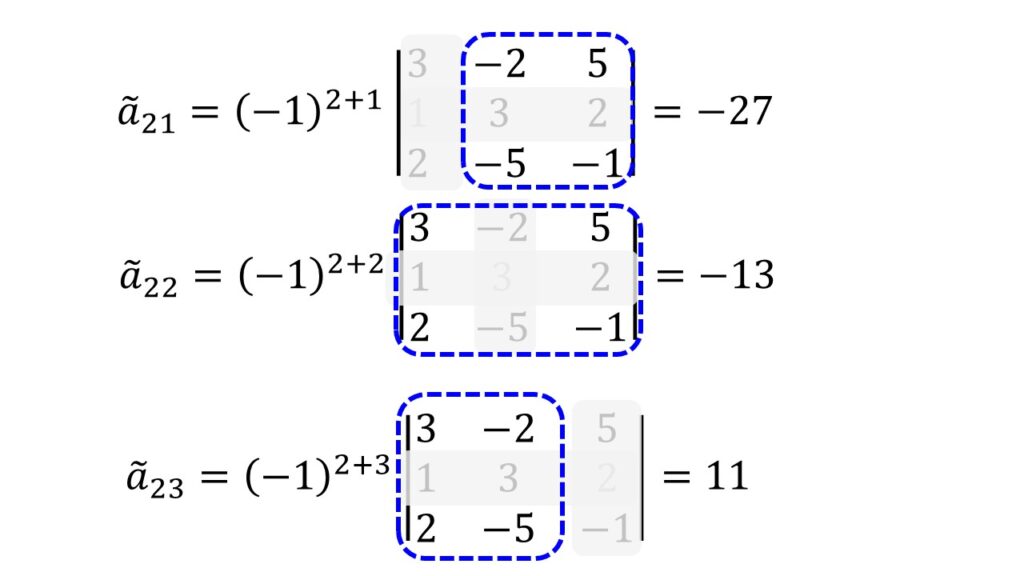

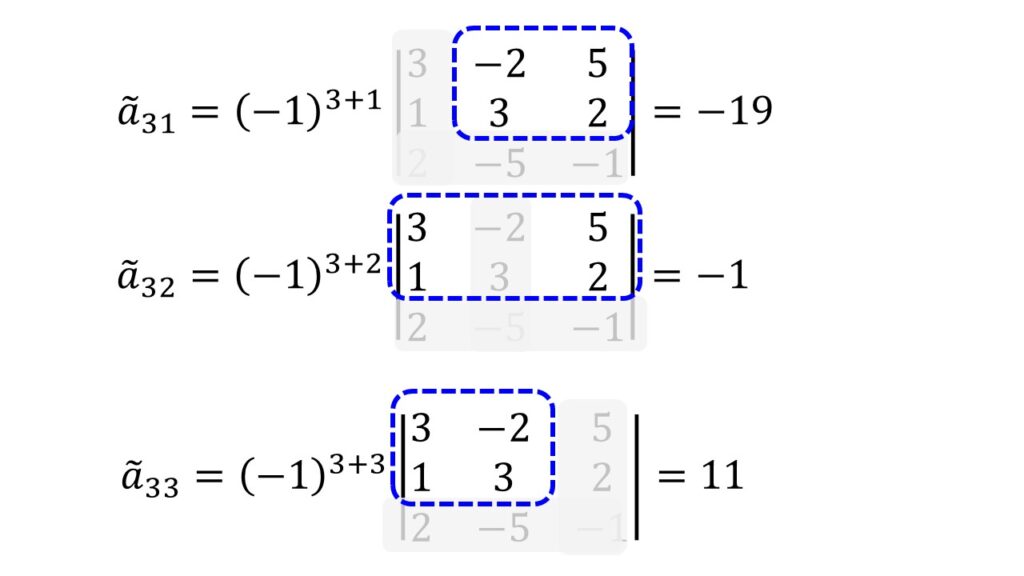

よって余因子行列$\tilde{A}$は、
\tilde{A}&=\underset{転置行列であることに注意}{{}^t\!\begin{pmatrix}
\tilde{a}_{11} &\tilde{a}_{12}&\tilde{a}_{13} \\
\tilde{a}_{21} &\tilde{a}_{22}&\tilde{a}_{23} \\
\tilde{a}_{31} &\tilde{a}_{32}&\tilde{a}_{33}
\end{pmatrix}}\\
&=\begin{pmatrix}
\tilde{a}_{11} &\tilde{a}_{21}&\tilde{a}_{31} \\
\tilde{a}_{12} &\tilde{a}_{22}&\tilde{a}_{32} \\
\tilde{a}_{13} &\tilde{a}_{23}&\tilde{a}_{33}
\end{pmatrix}\\
&=\begin{pmatrix}
7 &-27&-19 \\
5 &-13&-1 \\
-11 &11&11
\end{pmatrix}\tag{4}
\end{align*}
逆行列$A^{-1}=\frac{1}{|A|}\tilde{A}$なので、$|A|=-44$のマイナスも余因子行列の中に入れてやると、
A^{-1}&=\frac{1}{|A|}\tilde{A}\\
&=\frac{1}{44}\begin{pmatrix}
-7 &27&19 \\
-5 &13&1 \\
11 &-11&-11
\end{pmatrix}
\end{align*}
本当に逆行列が正しく計算できたかどうかは、下記のサイトで確認しました。


正しく計算できていますね。
また、(4)で求めた逆行列が正しいかどうかは$AA^{-1}=E$($E$は単位行列)となるかどうかを計算してみても良いですね。
まとめ
本記事では以下の3行3列の正方行列Aの逆行列を余因子行列を使って例題演習を行いました。
逆行列を求める手順は以下となっています。
逆行列を求める方法は他に「クラメルの公式」や「拡大係数行列」を使う方法があります。
次回は拡大係数行列を使った逆行列の求め方を紹介します(^^)/
参考にする参考書はこれ
当ブログでは、以下の2つの参考書を読みながらよく使う内容をかいつまんで、一通り勉強すればついていけるような内容を目指していこうと思います。
大事なところをかいつまんで、「これはよく使うよな。これを理解するためには補足で説明をする」という調子で進めていきます(^^)/


























(3)の部分の計算、一行目、2x(-2)x2です
ご指摘ありがとうございます。