【内積とは（スカラー積とは）】具体的な計算方法と力学の仕事を理解する。

こんにちは(@t_kun_kamakiri)(^^)/

前回では、「ベクトルの和と実数倍」についての記事をまとめました。

前回の記事はこちら

【はじめて学ぶ線形代数(1回)】ベクトルの和と実数倍

今回も引き続き、高校生で習うベクトルについて復習をしておきましょう。

本記事の内容

内積（スカラー積）
内積の物理での例

これから線形代数を学ぶ学生や社会人のために「役に立つ内容にしたい」という思いで記事を書いていこうと考えています。

ベクトルにはスカラー積とベクトル積がある
内積（スカラー積）
1. ベクトル\(\boldsymbol{a}=(a_{1},a_{2},a_{3})\)と\(\boldsymbol{b}=(b_{1},b_{2},b_{3})\)の内積
内積0は、2つのベクトルが直交していることを意味する
内積の物理の例：仕事量
まとめ
参考にする参考書はこれ

ベクトルにはスカラー積とベクトル積がある

2つの線形独立な任意のベクトル\(\boldsymbol{a}\)と\(\boldsymbol{b}\)に対して、積を考えるとき、次の2つの積があります。

内積と外積

内積（スカラー積）：\(\boldsymbol{a}\cdot \boldsymbol{b}\)
外積（ベクトル積）：\(\boldsymbol{a}\times \boldsymbol{b}\)

高校生の範囲では、内積は習うでしょうか。

でも、外積はほとんどの高校生が履修単元に入っておらず大学ではじめて学ぶか、気の利かせた高校の先生がこっそり「便利だから・・・」と教えている場合もあります。

ともかく、内積は習うとしても、外積は習っていない可能性がありますね。
外積は次回の記事に書くとして、まずは内積から解説をします(^^)/

内積（スカラー積）

2つの線形独立な任意のベクトル\(\boldsymbol{a}\)と\(\boldsymbol{b}\)に対して、積を考えるとき、内積は以下のように定義されます。
線形独立とは、\(\boldsymbol{a}\)と\(\boldsymbol{b}\)が違う方向を向いている場合と考えておけば良いでしょう。
（\(\boldsymbol{a}=c\boldsymbol{b}\)だと互いに向きは同じなので、線形独立ではなりません。）

内積（スカラー積）

\begin{align*}
\boldsymbol{a}\cdot \boldsymbol{b}=\left |\boldsymbol{a}\right|\left |\boldsymbol{b}\right|\cos\theta\tag{1}
\end{align*}

2つのベクトルの積を考えたとき、互いに向きが異なると、どう掛け算しようかなってなります・・・・

方法としては、どちらか片方のベクトルを相手側のベクトルに垂線を下した方向に射影して掛け算を行う方法ですね。
今回は\(\boldsymbol{a}\)を\(\boldsymbol{b}\)の方向に射影します。

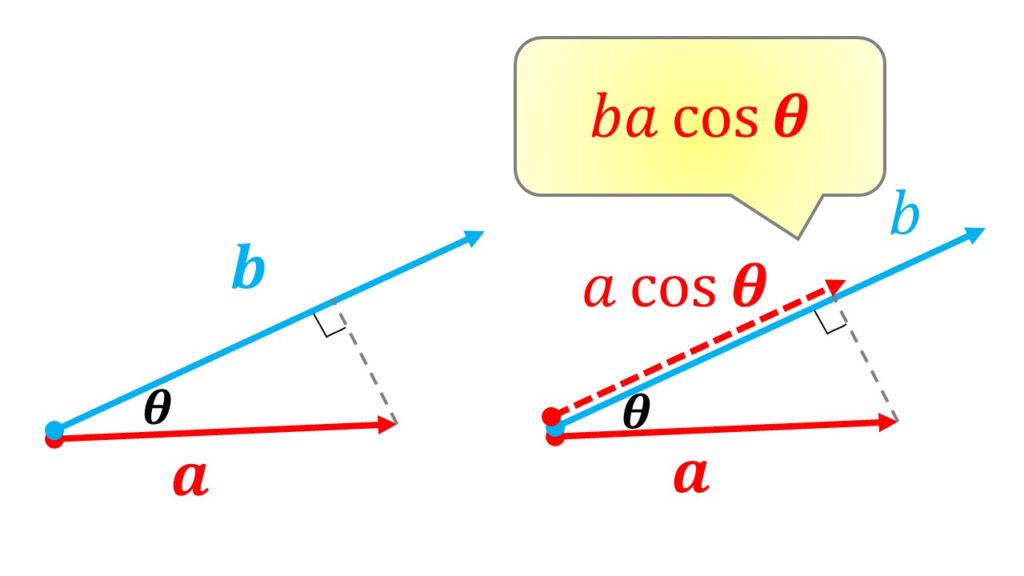
そうすると、\(\boldsymbol{a}\)のベクトルは大きさが\(a\cos\theta\)になって、向きが\(\boldsymbol{b}\)と同じになります。

このように向きをそろえて掛け算をすると、

\begin{align*}
ab\cos\theta\tag{2}
\end{align*}

となります。

これを内積と定義して以下のようになっていたわけです。

\begin{align*}
\boldsymbol{a}\cdot \boldsymbol{b}=\left |\boldsymbol{a}\right|\left |\boldsymbol{b}\right|\cos\theta\tag{3}
\end{align*}

内積の結果は、「向き」という概念がなくなり、「大きさのみ（スカラーのみ）」になっているため、スカラー積と呼ばれています。

内積のその他の、表記には、

\begin{align*}
(\boldsymbol{a}, \boldsymbol{b})=\boldsymbol{a}\cdot \boldsymbol{b}=\left |\boldsymbol{a}\right|\left |\boldsymbol{b}\right|\cos\theta\tag{4}
\end{align*}

などがあります。

2つの線形独立ではない場合は、\(\boldsymbol{a}=c\boldsymbol{b}\)となります。この場合は、向きとかは関係なく大きさのみが意味を持つので、\(\boldsymbol{a}\cdot\boldsymbol{b}=c|b|^2\)となります。

ベクトル\(\boldsymbol{a}=(a_{1},a_{2},a_{3})\)と\(\boldsymbol{b}=(b_{1},b_{2},b_{3})\)の内積

任意の2つのベクトルの成分が\(\boldsymbol{a}=(a_{1},a_{2},a_{3})\)と\(\boldsymbol{b}=(b_{1},b_{2},b_{3})\)であるとき、内積の計算はどうなるのかというと、

\begin{align*}
\boldsymbol{a}\cdot \boldsymbol{b}=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}\tag{5}
\end{align*}

各成分で掛け算を行い、その和を計算することで内積が計算できます。
つまり、ベクトルは「向き」と「大きさ」を持っていますが、各成分は独立で掛け算を行って・・・そして和をとる
ということですね。

単位ベクトル\(\boldsymbol{e}_{1}=(1,0,0)\),\(\boldsymbol{e}_{2}=(0,1,0)\),\(\boldsymbol{e}_{3}=(0,0,1)\)とすると、任意のベクトル\(\boldsymbol{a}\)は以下のように書けます。

\begin{align*}
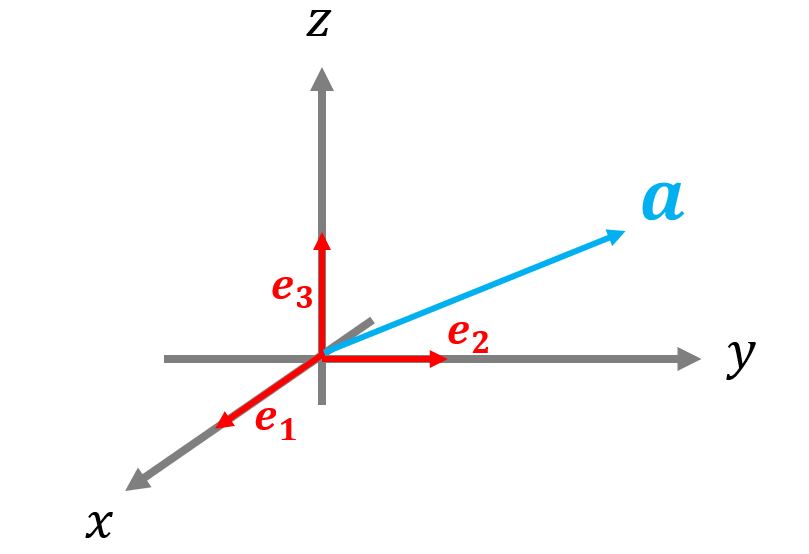
\boldsymbol{a}=a_{1}\boldsymbol{e}_{1}+a_{2}\boldsymbol{e}_{2}+a_{3}\boldsymbol{e}_{3}=\sum_{i=1}^{3}a_{i}\boldsymbol{e}_{i}\tag{6}
\end{align*}

ここで、各単位ベクトルの内積は以下のように定義しておきます。

\begin{align*}
\boldsymbol{e}_{i}\cdot\boldsymbol{e}_{j}=\delta _{ij}\tag{7}
\end{align*}

\(\delta_{ij}\)はクロネッカーデルタと呼ばれているもので、同じ単位ベクトル同士なら１で異なる単位ベクトルなら0になるものです。

このように(7)を定義しておくと、任意のベクトル\(\boldsymbol{a}\)と\(\boldsymbol{b}\)の内積は、

\begin{align*}
\boldsymbol{a}\cdot\boldsymbol{b}&=\big(a_{1}\boldsymbol{e}_{1}+a_{2}\boldsymbol{e}_{2}+a_{3}\boldsymbol{e}_{3}\big)\big(b_{1}\boldsymbol{e}_{1}+b_{2}\boldsymbol{e}_{2}+b_{3}\boldsymbol{e}_{3}\big)\\
&=a_{1}b_{1}\boldsymbol{e}_{1}\cdot\boldsymbol{e}_{1}+a_{1}b_{2}\boldsymbol{e}_{1}\cdot\boldsymbol{e}_{2}+a_{1}b_{3}\boldsymbol{e}_{1}\cdot\boldsymbol{e}_{3}\\
&+a_{2}b_{1}\boldsymbol{e}_{2}\cdot\boldsymbol{e}_{1}+a_{2}b_{2}\boldsymbol{e}_{2}\cdot\boldsymbol{e}_{2}+a_{2}b_{3}\boldsymbol{e}_{2}\cdot\boldsymbol{e}_{3}\\
&+a_{3}b_{1}\boldsymbol{e}_{3}\cdot\boldsymbol{e}_{1}+a_{3}b_{2}\boldsymbol{e}_{3}\cdot\boldsymbol{e}_{2}+a_{3}b_{3}\boldsymbol{e}_{3}\cdot\boldsymbol{e}_{3}\\
&=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}\tag{8}
\end{align*}

と結局各成分の掛け算の和になります。

内積0は、2つのベクトルが直交していることを意味する

2つの任意のベクトル\(\boldsymbol{a},\boldsymbol{b}\)の内積を計算して0になったら、それはとても重要な情報を持った結果です。

内政の定義から、

\begin{align*}
\boldsymbol{a}\cdot \boldsymbol{b}=\left |\boldsymbol{a}\right|\left |\boldsymbol{b}\right|\cos\theta＝０\tag{9}
\end{align*}

ということは、\(\cos\theta=0\)、すなわち\(\theta=90°\)であることを意味しています。

つまり、ベクトル\(\boldsymbol{a},\boldsymbol{b}\)は互いに直交しているということになります。

「内積0」の結果は、物理的な考察をするうえでもとても重要な意味を持っている場合が多いです。

カマキリ

ベクトルの内積の基本は終わりです。

ここからは、ベクトルの内積（スカラー積）が物理学の中でどのように使われているのかを見てみます。

内積の物理の例：仕事量

内積を物理で使う場面はかなり多くあります。

ここでは、物理で内積を使う場面の例として「仕事量」を紹介します。
力学における仕事量の定義としては、「力×移動距離」です。

ただし、この時の力は移動距離に対して有効な力という意味ですね。
どういう意味かというと、移動距離に対して力が垂直方向に力を加えても何も仕事量を生み出さないというわけです。

少し意味がわかるように絵を描いています。

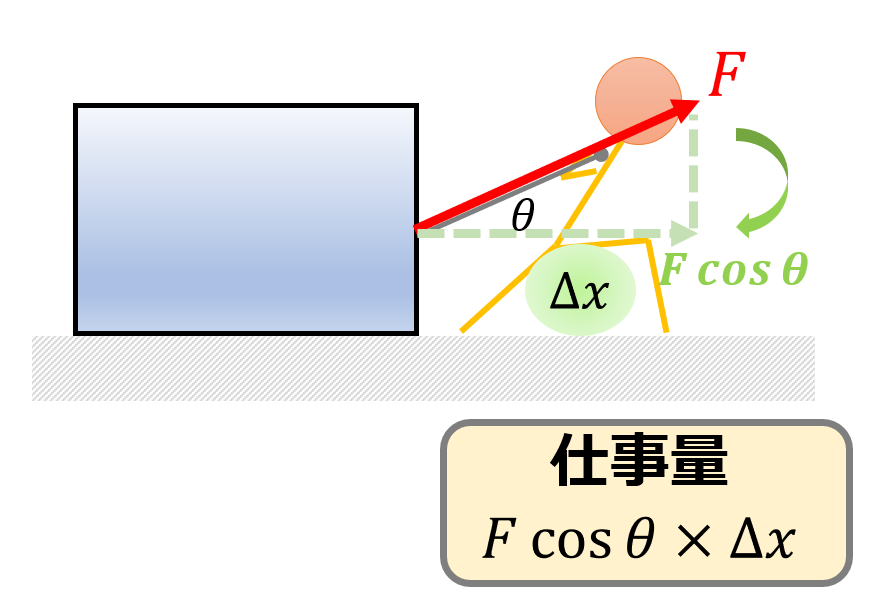
これは、人が物体を引っ張っている絵です。
移動距離に対して角度\(\theta\)で、力\(F\)で引っ張っているイメージです。

このとき有効な力というのは\(F\)そのものではなく、移動距離の方向に射影した力\(F\cos\theta\)です。

なので、このときの仕事量は、

\begin{align*}
W=F\cos\theta \times \Delta x\tag{10}
\end{align*}

となります。

これは(3)で定義した内積計算そのものですよね。

なので(10)は以下のようにベクトルの内積として書いてもよいということになります。

\begin{align*}
W=\boldsymbol{F}\cdot \Delta \boldsymbol{x}\tag{11}
\end{align*}

そして、計算された仕事量は「スカラー」ですね。

力の方向が移動距離に対して\(90°\)なら\(\cos 90°=0\)となるため仕事量が0であることがわかりますね。

このように、仕事量は内積で記述できるということがわかります。

まとめ

本記事では内積についての解説をしました。

本記事の内容

内積（スカラー積）
内積の物理での例

内積の表記は以下となります。

\begin{align*}
(\boldsymbol{a}, \boldsymbol{b})=\boldsymbol{a}\cdot \boldsymbol{b}=\left |\boldsymbol{a}\right|\left |\boldsymbol{b}\right|\cos\theta\tag{4}
\end{align*}

内積は物理の仕事量の計算に使われます。

\begin{align*}
W=\boldsymbol{F}\cdot \Delta \boldsymbol{x}\tag{11}
\end{align*}