こんにちは(@t_kun_kamakiri)(^^)/
前回は線形独立と線形従属について解説を行いました。
今回は線形代数で超重要な固有値と固有ベクトルのお話をします。
固有値方程式から求まる固有値と固有ベクトルを知ることで対角行列や基底変換など面白い内容が待っています(^^)
固有値と固有ベクトルを理解する。
そのあとの対角行列や基底変換につながる内容となっています!
これから線形代数を学ぶ学生や社会人のために「役に立つ内容にしたい」という思いで記事を書いていこうと考えています。
- 行列をはじめて習う高校生・大学生
- 仕事で行列を使うけど忘れてしまった社会人
この記事の内容をマスターして線形独立と線形従属を理解しましょう(^^)
固有値方程式
理解をしやすいように2次元で考えます。
2次元ベクトル$x=\begin{pmatrix}
2 \\
1 \\
\end{pmatrix}$に行列$A=\begin{pmatrix}
4 & -2 \\
1 & 1 \\
\end{pmatrix}$を作用させてできるベクトルを$x^{\prime}$とします。
一般的な形で書くと以下のようになります。
A\boldsymbol{x}=\boldsymbol{x}^{\prime}\tag{1}
\end{align*}
これを具体的に計算をすると、
A\boldsymbol{x}&=
\begin{pmatrix}
4 & -2 \\
1 & 1 \\
\end{pmatrix}\begin{pmatrix}
1 \\
2 \\
\end{pmatrix}\\
&=\begin{pmatrix}
4\times 1 & -2\times 2 \\
1\times 1 & 1\times 2 \\
\end{pmatrix}\\
&=\begin{pmatrix}
0 \\
3 \\
\end{pmatrix}\tag{2}
\end{align*}
となるので$x^{\prime}=\begin{pmatrix}
0 \\
3 \\
\end{pmatrix}$ になります。
これを絵で描くと以下のようになります。
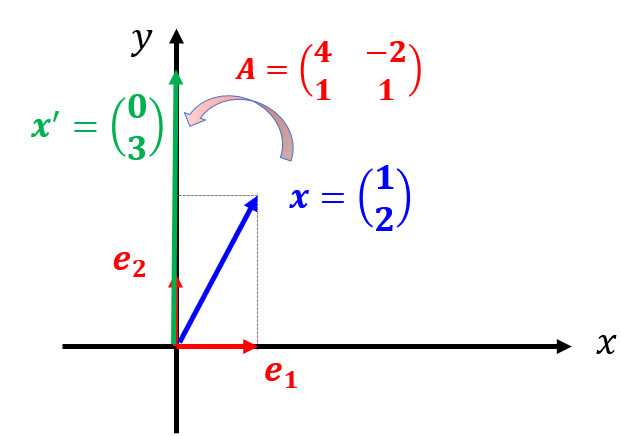
2次元ベクトル$\boldsymbol{x}$に行列$A$を作用させると別の2次元ベクトル$\boldsymbol{x}^{\prime}$に変換されたことになります。
このように行列$A$を別のベクトルに作用させると大きさも向きも異なるベクトルに変換されることになります。つまり、行列$A$はベクトルを異なるベクトルに変換する変換行列ということです。
ここで、「行列$A$を作用させても向きが変わらず大きさだけが変わるベクトルを見つけることができないか?」ということを考えます。
絵にすると↓こんな感じ。向きは変わらず大きさだけが変わる変換です。
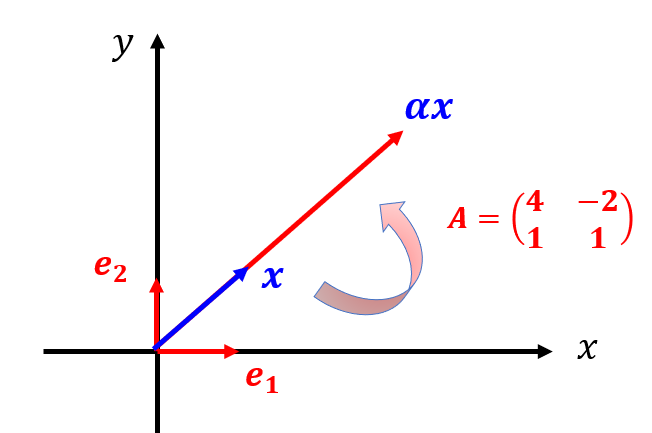
このような都合の良いベクトルを見つけることができれば便利なことが多いため、行列$A$に対して以下のような関係にあるベクトル$\boldsymbol{x}$と定数$\alpha$とを探してみましょう。
A\boldsymbol{x}=\alpha \boldsymbol{x}\tag{3}
\end{align*}
これが固有値方程式と呼ばれるものです。
このとき$\boldsymbol{x} \neq 0$という条件を忘れてはいけません。
固有値と固有ベクトル
固有値方程式
A\boldsymbol{x}=\alpha \boldsymbol{x}\tag{3}
\end{align*}
から得られる$\boldsymbol{x}$を固有ベクトル、$\alpha$を固有値といいます。
固有値を求める
まだ話をわかりやすくするために2次元で考えることにします。
(3)を変形して以下のようにします。
(A-\alpha E)\boldsymbol{x}=0\tag{4}
\end{align*}
※単位行列$E=\begin{pmatrix}
1&0 \\
0&1 \\
\end{pmatrix}$
$\boldsymbol{x} \neq 0$であるためには$(A-\alpha E)$が逆行列を持ってはいけないということになりますね。
わかりやすく$B=(A-\alpha E)$と置くと、$B\boldsymbol{x}=0$となるので、もし$B$が逆行列$B^{-1}$を持つなら左から$B^{-1}$を作用させることで$B^{-1}B\boldsymbol{x}=0\Leftrightarrow E\boldsymbol{x}=0$となり$\boldsymbol{x}=0$となってしまいます。
ということはやはり$(A-\alpha E)$は逆行列を持ってはいけないということになります。
「逆行列を持たない条件は行列式$|A-\alpha E|$を計算して0であること」を思い出しましょう。
逆行列を持つための条件、持たないための条件については復習したい方のために記事を添付しておきます。
|A-\alpha E|=0\tag{5}
\end{align*}
\begin{vmatrix}
4-\alpha& -2\\
1&1-\alpha \\
\end{vmatrix}\tag{6}
\end{align*}
を計算します。
$(4-\alpha)(1-\alpha)-(-2\times2)=0$となるので、$\alpha^2-5 \alpha +6=0$を解けば、$\alpha=2,3$が求まりますね。
これで固有値が求まりました。
後で固有値と固有ベクトルの組がわかるように$\alpha_{1}=2,\alpha_{2}=3$と置いて置きます。
※あとでもう一度書きますが、注意すべき点は$A-\alpha E$の逆行列を考えているということはもともとの$A$は正方行列(行と列が同じ数)であるという条件付きだということですね。なぜなら逆行列というのは正方行列にのみ定義ができたからです。
固有ベクトルを求める
固有値が求まったのでそれに対応する固有ベクトルを求めましょう。
$A\boldsymbol{x}=\alpha \boldsymbol{x}$に先ほど求めた$\alpha_{1},\alpha_{2}$を代入して固有ベクトル$\boldsymbol{x}=\begin{pmatrix}
x_{1}\\
x_{2}\\
\end{pmatrix}$を求めれば良いですね。
(1)$\alpha_{1}=2$のとき
$\alpha_{1}$に対する固有ベクトルを$\boldsymbol{x}_{1}$とするとき、
A\boldsymbol{x}_{1}=\alpha_{1} \boldsymbol{x}_{1}
\end{align*}
なので行列で書くと、
\begin{pmatrix}
4-\alpha_{1}& -2\\
1&1-\alpha_{1}\\
\end{pmatrix}\begin{pmatrix}
x_{1}\\
x_{2}\\
\end{pmatrix}=0\tag{7}
\end{align*}
$\alpha_{1}=2$を代入すると、
\begin{pmatrix}
4& -2\\
1&-1\\
\end{pmatrix}\begin{pmatrix}
x_{1}\\
x_{2}\\
\end{pmatrix}=0\tag{8}
\end{align*}
行列ではなく連立方程式で書くと以下のようになります。
\left\{\begin{matrix}
4x_{1}-2x_{2}=0\\
x_{1}-2x_{2}=0
\end{matrix}\right.
\end{align*}
よく見ると1つ目の式と2つ目の式は定数倍だけ違うだけで2つ目の式を2で割ると全く同じ形になりますよね。
これは当然の結果です。なぜなら$(A-\alpha E)=\begin{pmatrix}
4-\alpha& -2\\
1&1-\alpha\\
\end{pmatrix}$が逆行列を持たないという条件で$\alpha_{1},\alpha_{2}$を求めたのですから独立の式にはならないんですよね。
【なぜ行列式の計算するのか?】逆行列を持つ条件とは。
の「逆行列が存在しないとはどういうことか?イメージで解説する」をご参考ください。
$x_{1} = x_{2}=k_{1}とおく$と求まりますので、固有値$\alpha_{1}=2$に対する固有ベクトルは、
=\begin{pmatrix}
x_{1}\\
x_{2}\\
\end{pmatrix}=k_{1}\begin{pmatrix}
1\\
1\\
\end{pmatrix}\tag{9}
\end{align*}
と求まります。
k_{1}は任意の値でも成り立つので$A\boldsymbol{x}_{1}=\alpha_{1} \boldsymbol{x}_{1}$を満たすので今回は簡単に$k_{1}=1$としておきましょう。
※$|\boldsymbol{x}_{1}|=k_{1}^2\sqrt{1^2+1^2}=k_{1}^2\sqrt{2}$となることから、$|\boldsymbol{x}_{1}|$を単にベクトルにするために$k_{1}=\frac{1}{\sqrt{2}}$とすることが多いですが、今回は$k_{1}=1$として話を進めます。
(2)$\alpha_{2}=3$のとき
$\alpha_{2}$に対する固有ベクトルを$\boldsymbol{x}_{2}$とするとき、
A\boldsymbol{x}_{2}=\alpha_{2} \boldsymbol{x}_{2}
\end{align*}
なので行列で書くと、
\begin{pmatrix}
4-\alpha_{2}& -2\\
1&1-\alpha_{2}\\
\end{pmatrix}\begin{pmatrix}
x_{1}\\
x_{2}\\
\end{pmatrix}=0\tag{10}
\end{align*}
$\alpha_{2}=3$を代入すると、
\begin{pmatrix}
1& -2\\
1&-2\\
\end{pmatrix}\begin{pmatrix}
x_{1}\\
x_{2}\\
\end{pmatrix}=0\tag{11}
\end{align*}
行列ではなく連立方程式で書くと以下のようになります。
\left\{\begin{matrix}
x_{1}-2x_{2}=0\\
x_{1}-2x_{2}=0
\end{matrix}\right.
\end{align*}
先ほど同様に2式は全く同じ形になりますよね。
$x_{1} = 2x_{2}=2k_{2}とおく$と求まりますので、固有値$\alpha_{2}=3$に対する固有ベクトルは、
=\begin{pmatrix}
x_{1}\\
x_{2}\\
\end{pmatrix}=k_{2}\begin{pmatrix}
2\\
1\\
\end{pmatrix}\tag{11}
\end{align*}
と求まります。
$k_{2}$についても$k_{1}$同様$k_{2}=1$としておきます。
まとめと、
図示するとこのようになります。
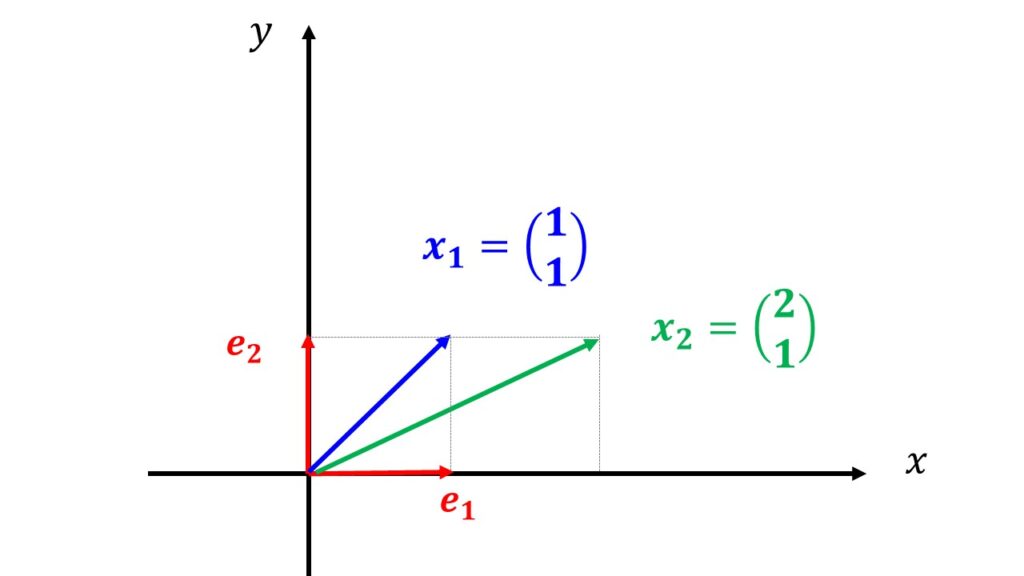
$\boldsymbol{x}_{1}$と$\boldsymbol{x}_{2}$は見るからに互いに独立なベクトルですよね。
前回の記事で解説した互いに線形独立なベクトルです。
今回は図でイメージしやすいように2次元ベクトルで考えましたが、実は一般的に$n$次元ベクトルに対しても固有値方程式から求まった異なる固有値に対する固有ベクトルは互いに線形独立な関係にあることを示すことができるのです。
※補足
固有値が$0$となる場合がありますが、$|A-\alpha E|=0$から$|A|=0$となるだけで固有値が$0$でも零ベクトルでない固有ベクトルが存在することはあります。
異なる固有値に対する固有ベクトルは線形独立
手書きではありますが証明を載せておきます。


線形変換とは
こちらも手書きですが追々きれいにまとめなおします_(._.)_



まとめ
本記事では固有値方程式から固有値と固有ベクトルを求めました。
また、異なる固有値に対する固有ベクトルは線形独立であるというのを証明しました。
固有値と固有ベクトルを求めると何が嬉しいのと思うかもしれません。一つ利点を挙げておくと、固有ベクトル$\boldsymbol{x}_{1}$,$\boldsymbol{x}_{2}$を基底に取るような線形空間を考えると行列$A$が対角行列になります。
今までは線形空間は考えやすくするために基底を$\boldsymbol{e}_{1}=\begin{pmatrix}
1\\
0\\
\end{pmatrix}$と$\boldsymbol{e}_{2}=\begin{pmatrix}
0\\
1\\
\end{pmatrix}$を考えていました。
このとき行列$A\boldsymbol{x}=
\begin{pmatrix}
4 & -2 \\
1 & 1 \\
\end{pmatrix}$という変換行列は全ての行と列に数字が入っているので$A\boldsymbol{x}$を計算しようものなら行列計算が面倒になりますよね。$A$が2行2列の行列ならそれほど手間ではありませんが、100行100列ともなると$A\boldsymbol{x}$のひとつの要素で100回の掛け算を行うので、それが100行あると100×100回掛け算をすることになります。
さらに$AB$のような100行100列どうしの行列の積だと、一つの要素で100個の掛け算、さらに$AB$の行列は100行100列ですから、100×100×100回掛け算をすることになります。考えただけでも途方もないですね。
これは空間を作るための基底を別のものに変えて、その基底での$A$に対応する行列が$A^{\prime}=\begin{pmatrix}
\alpha_{1} & 0\\
0 & \alpha_{2} \\
\end{pmatrix}$のような対角成分にのみ値を持つ対角行列になってくれたらなんて嬉しいことでしょう。
$A^{\prime}=\begin{pmatrix}
\alpha_{1} & 0\\
0 & \alpha_{2} \\
\end{pmatrix}\begin{pmatrix}
x_{1}\\
x_{2}
\end{pmatrix}=\begin{pmatrix}
\alpha_{1}x_{1}\\
\alpha_{2}x_{2}
\end{pmatrix}$のように簡単に計算できますよね。
基底を変えて$A$に対応する行列が対角行列になってくれたら、例えば100行100列の行列計算でもそのほとんどが0になるので100回の掛け算の計算で済みます。
そして計算し終わったらもとの基底に戻す変換を行えばよいですよね。
次回は「対角行列と基底変換」の話をします。
今回使った固有値・固有ベクトルをがっつり使うので本記事の内容をしっかりと押さえておきましょう。
参考にする参考書はこれ
当ブログでは、以下の3つの参考書を読みながらよく使う内容をかいつまんで、一通り勉強すればついていけるような内容を目指していこうと思います。
大事なところをかいつまんで、「これはよく使うよな。これを理解するためには補足で説明をする」という調子で進めていきます(^^)/