前回では、大学入りたてホヤホヤの新入生に向けて線形代数の記事を書いていくよという宣言をしました。
今回は、線形代数の入りとしてまずは高校生で習うベクトルについて復習をしておきましょう。
- ベクトルとは
- ベクトルの和
- ベクトルの実数倍
これから線形代数を学ぶ学生や社会人のために「役に立つ内容にしたい」という思いで記事を書いていこうと考えています。
ベクトルとは
ベクトルとは「向き」と「大きさ」を持った量です。

始点\(P\)、終点\(Q\)までを指す向きに方向を持ち、PQの長さが大きさということになります。
これをベクトル表記で、
\vec{A}=\vec{PQ}\tag{1}
\end{align*}
ベクトル表記は、太文字で書くこともあるので、参考書で太文字で書かれているものに関しては、ベクトル表記であると思いましょう。
\boldsymbol{a}=\vec{A}=\vec{PQ}\tag{2}
\end{align*}
と書く場合が多いです。
ちなみに始点は、どこにとっても良いので、「向き」と「大きさ」さえ同じであれば同じベクトルということになります。
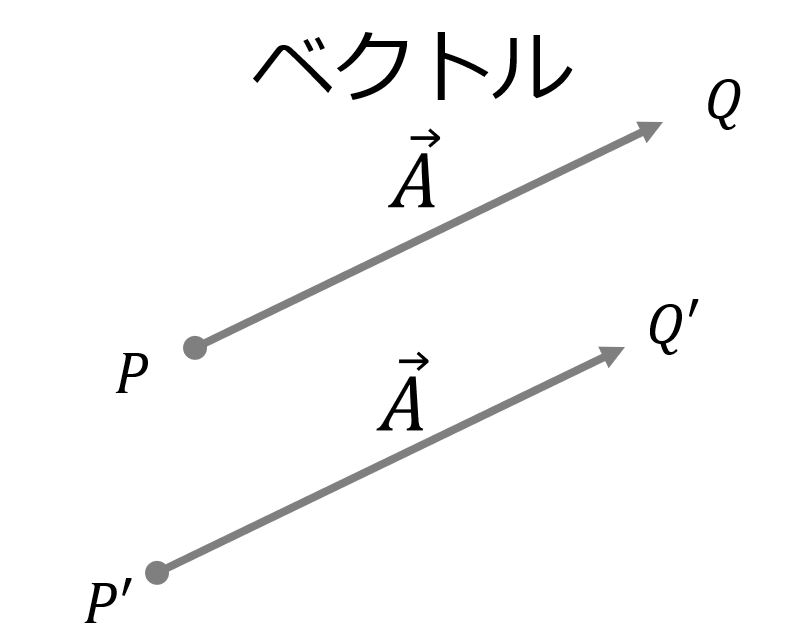
\vec{PQ}=\vec{P^{\prime}Q^{\prime}}\tag{3}
\end{align*}
本当にイコールとして良いのかについては、数学の一分野でもある「集合」できちんとお話をしたいと思います。
ここでは「向き」と「大きさ」が同じであれば、始点の位置にはよらず同じベクトルになると言うことができるとしましょう。
ベクトルの和
始点\(P\)から終点\(Q\)までの方向を\(\vec{A}=\vec{PQ}\)と書きましたが、これは以下のように始点\(P\)から一旦\(Q^{\prime}\)に行き、その後\(Q\)に行くというルートを取った場合と同じになります。
(一直線に向かったか、遠回りしたかの違いですね)
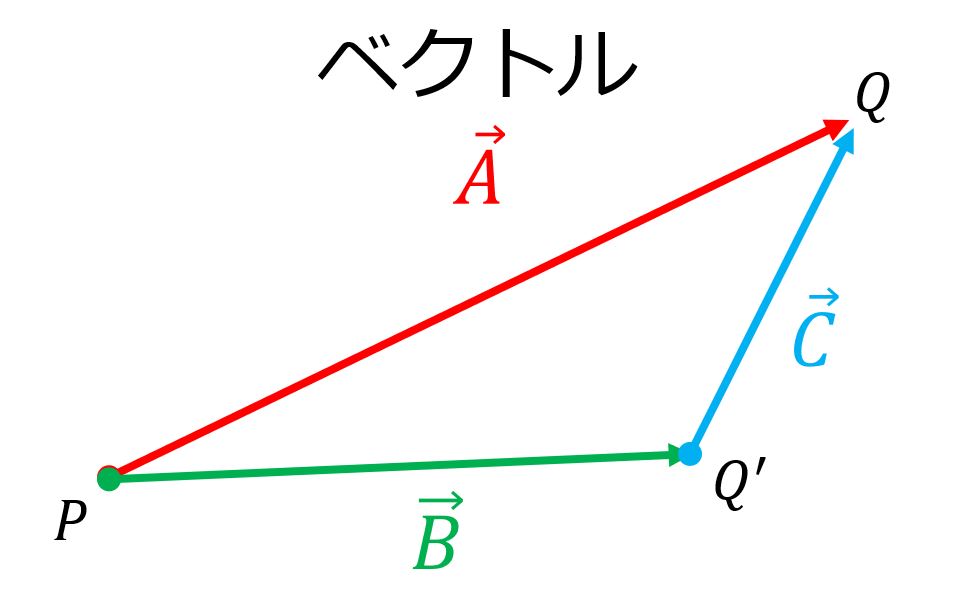
その時、\(PQ\)は、以下のような和で書くことができます。
\vec{PQ}=\vec{PQ^{\prime}}+\vec{Q^{\prime}Q}\tag{4}
\end{align*}
先ほど、ベクトルは始点にはよらず、「向き」と「大きさ」さえ同じであれば同じベクトルと書きました。
なので、始点を終点を\(\vec{PQ}\)と、二文字使うのではなく以下のように書きます。
- \(\vec{PQ}=\vec{A}\)
- \(\vec{PQ^{\prime}}=\vec{B}\)
- \(\vec{Q^{\prime}Q}=\vec{C}\)
そうすると、(4)は、
\vec{A}=\vec{B}+\vec{C}\tag{5}
\end{align*}
\boldsymbol{a}=\boldsymbol{b}+\boldsymbol{c}\tag{6}
\end{align*}
と書いても良いです。
ここで、ベクトルの加法に関する法則をまとめておきます。
- \(\boldsymbol{a}+\boldsymbol{b}=\boldsymbol{b}+\boldsymbol{a}\):交換法則
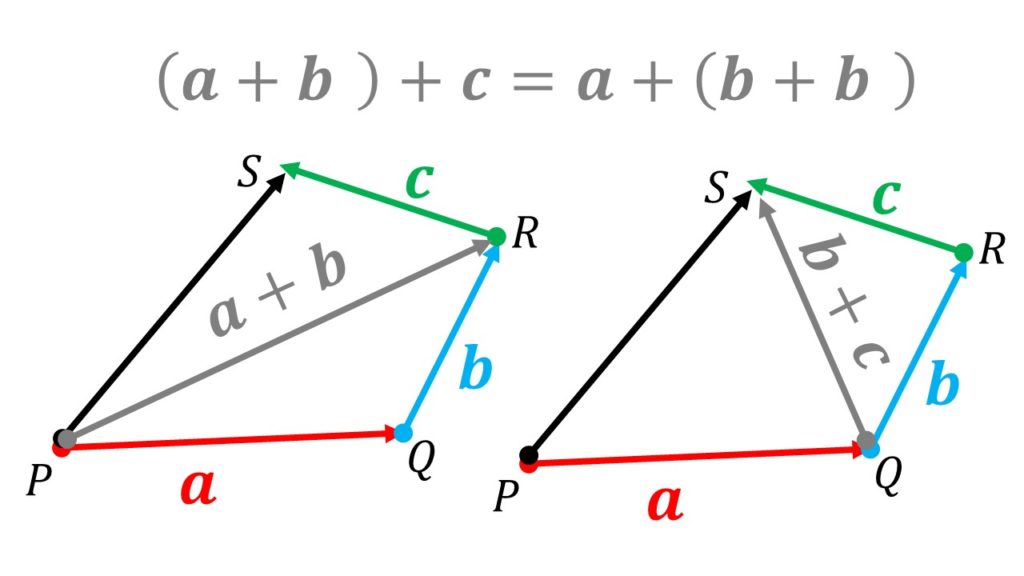
- \((\boldsymbol{a}+\boldsymbol{b})+\boldsymbol{c}=\boldsymbol{a}+(\boldsymbol{b}+\boldsymbol{c})\):結合法則
- \(\boldsymbol{a}+\boldsymbol{0}=\boldsymbol{a}\)
結合法則は下記の絵を見ればわかるのではないでしょうか。
\(\boldsymbol{0}\)とは何かを説明してなかったですね。
\(\boldsymbol{0}\)は、「大きさ」が0で「向き」も無いベクトルで零ベクトルと呼ばれています。
数字の0に相当するベクトルですね。
ベクトルの実数倍
今度は、ベクトルの実数倍を考えましょう。
- ベクトルを2倍にすると、大きさだけ2倍になって、方向は変わらない。
- ベクトルを\(\frac{1}{3}\)倍にすると、大きさだけ\(\frac{1}{3}\)倍になって、方向は変わらない。
- ベクトルを\(-1\)倍にすると、大きさだけ\(-1\)倍になって、方向は変わらない。
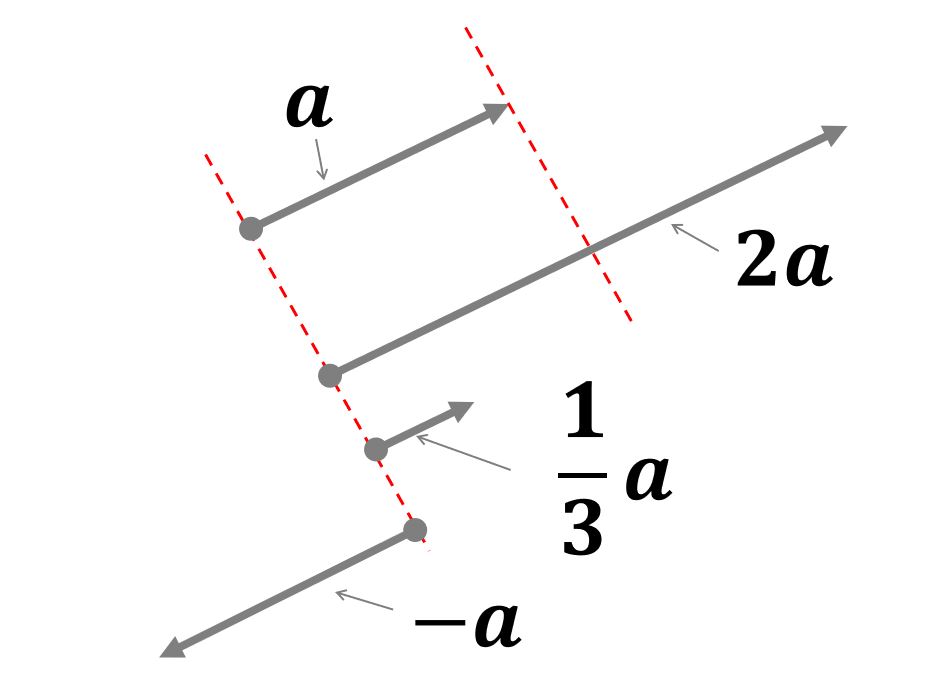
つまり、ベクトルを実数\(s\)倍にすると、大きさだけ\(s\)倍になって、方向は変わらないということとです。
ベクトルのマイナス倍はイメージがつかないかもしれませんが、方向が逆になるということです。
そこで実数倍に対しても以下のような法則が成り立ちます。
- \(c(\boldsymbol{a}+\boldsymbol{b})=c\boldsymbol{a}+c\boldsymbol{b}\)
- \((c+d)\boldsymbol{a}=c\boldsymbol{a}+d\boldsymbol{a}\)
- \((cd)\boldsymbol{a}=c(d\boldsymbol{a})\)
まとめ
本日は、線形代数の入りとして高校生でならうベクトルについて簡単に復習を行いました。
ベクトルは「大きさ」と「向き」を持った量であり、以下のような加法と実数倍の法則が成り立ちます。
- \(\boldsymbol{a}+\boldsymbol{b}=\boldsymbol{b}+\boldsymbol{a}\):交換法則
- \((\boldsymbol{a}+\boldsymbol{b}+\boldsymbol{c})=\boldsymbol{a}+(\boldsymbol{b}+\boldsymbol{c})\):結合法則
- \(\boldsymbol{a}+\boldsymbol{0}=\boldsymbol{a}\)
- \(c(\boldsymbol{a}+\boldsymbol{b})=c\boldsymbol{a}+c\boldsymbol{b}\)
- \((c+d)\boldsymbol{a}=c\boldsymbol{a}+d\boldsymbol{a}\)
- \((cd)\boldsymbol{a}=c(d\boldsymbol{a})\)
実現象はベクトルだらけ
物理学では、現象を数式で取り扱うとき、3次空間上のベクトル量で物理量を取り扱うことがほとんどです。
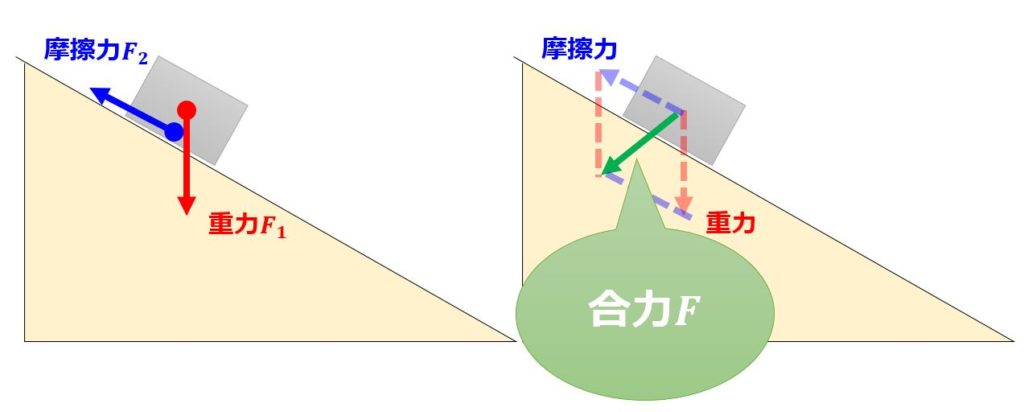
なので、運動方程式も、
m\frac{d^2\boldsymbol{x}}{dt^2}=\boldsymbol{F}_{1} +\boldsymbol{F}_{2}
\end{align*}
その他にも、次元が大きくなってくるとベクトルでは表現できず行列を使う場面が出てきます。
そうなったとき、線形代数で習う知識は大いに活かされるので、線形代数はめっちゃ重要だと感じれるでしょう(^^)/
参考にする参考書はこれ
一から順序立てて説明しようとすると膨大な時間がかかります。
当ブログでは、以下の2つの参考書を読みながらよく使う内容をかいつまんで、一通り勉強すればついていけるような内容を目指していこうと思います。
大事なところをかいつまんで、「これはよく使うよな。これを理解するためには補足で説明をする」という調子で進めていきます(^^)/