こんにちは(@t_kun_kamakiri)(^^)/
本記事では母集団と標本集団の違いについて高校生でもわかるように解説をします。
- 母集団と標本集団の違い
- 標本集団から統計量を計算する目的
- 標本集団から統計量を計算する
これから統計学を学ぶ学生や社会人のために「役に立つ内容にしたい」という思いで記事を書いていこうと考えています。
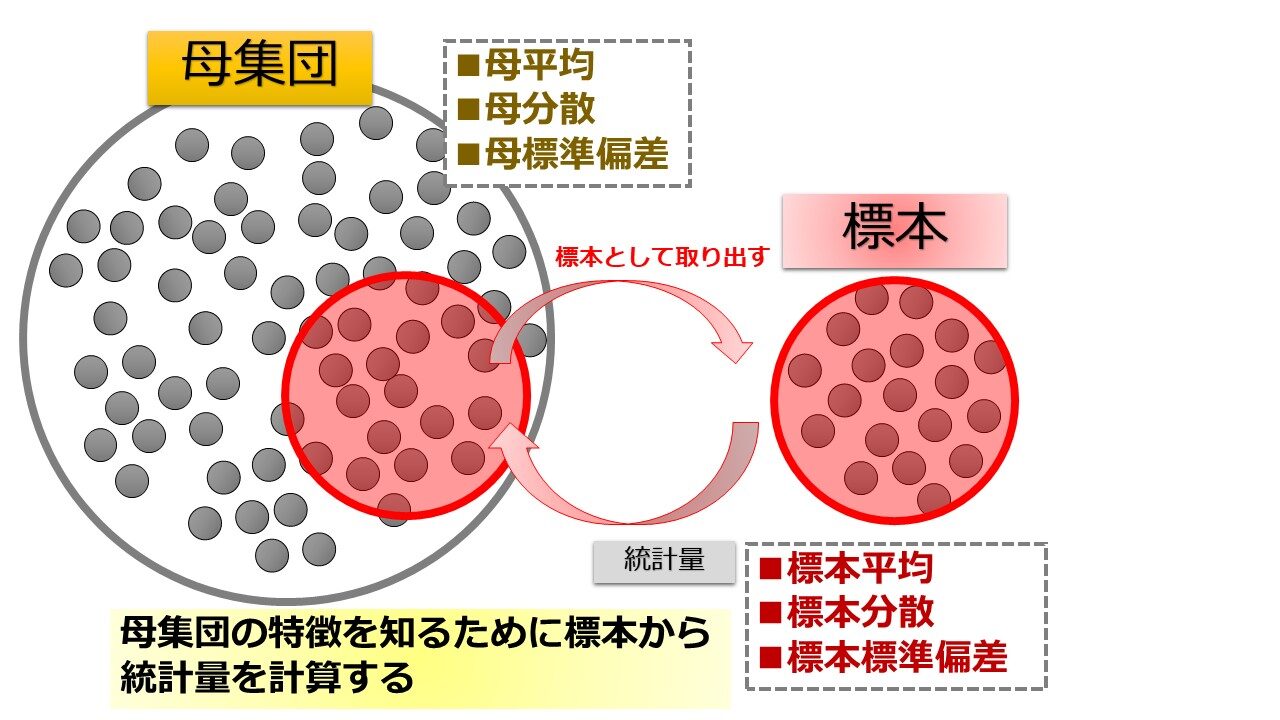
母集団と標本集団
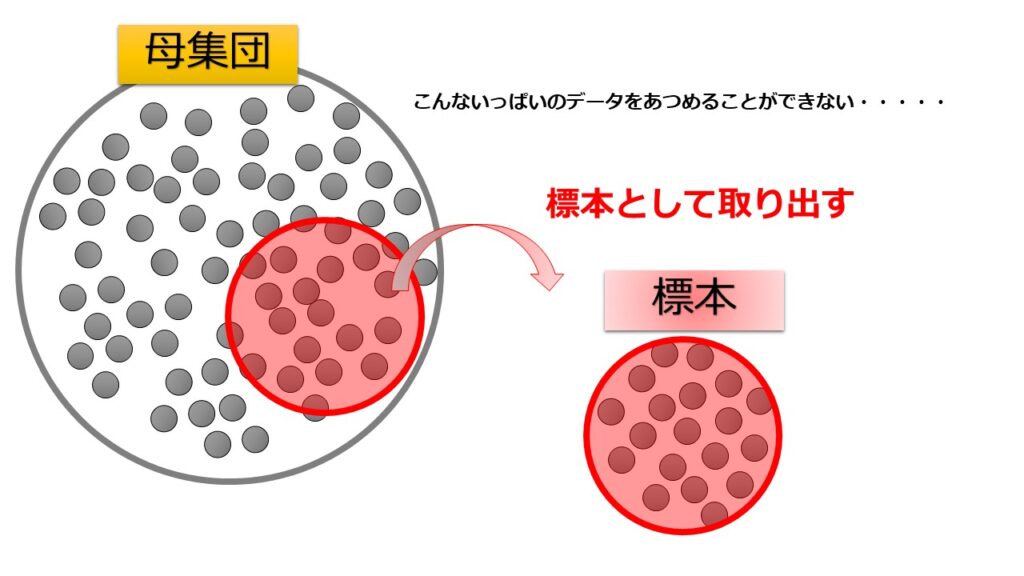
母集団とは「調査の対象となる集合全体」のことです。
一方、標本集団とは「母集団の部分集合」のことです。
例えば、母集団と標本集団の例として以下のものがあります。
| 母集団 | 標本集団 | |
| 身長 | 全小学生の身長 | 複数校の小学生の身長 |
| アンケート | 全30代の年収 | 街中のアンケートを受けた30代の年収 |
| 製品の重要 | 全製品Aの重量 | 数個抜き取った製品A |
全国の小学生の身長は文部科学省に記載がありますが、全30代の年収やある製造業の製品Aの質量をすべて調査するのは難しいし不可能ですよね。
本当は母集団のデータを集めたいがどうしようか?となるわけです。
こんな時に母集団の一部を抽出して標本として取り出すというのを行います。
このときのデータが標本集団です。
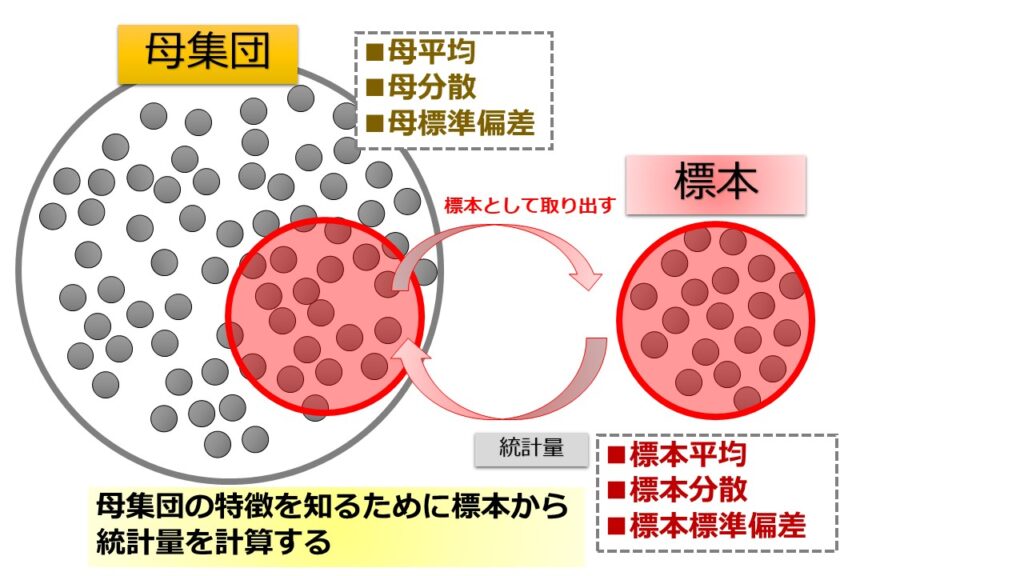
標本集団から「平均、分散、標準偏差」などを計算します。
この標本集団から得られたデータから計算される量がが統計量と呼ばれています。
でも、標本集団から得たデータが本当に母集団を表しているのかは怪しいですよね。
統計量を計算する目的
標本集団から抽出したデータから統計量を計算する目的は何か?
統計量を計算する目的は母集団の特徴を推測するため
母集団における特徴的な量を母数と言います。
- 母平均
- 母分散
- 母標準偏差
その他にも母集団の分布も特徴のひとつです。
- 母集団分布の形
- 母集団分布の中心位置
- 母集団分布の中心からの広がり具合
これらの母集団の量を知ることが統計的手法の目的です。
大事なのでもう一回言っておきます。
統計量は標本集団から求まり、統計量を計算する目的は母集団の特徴を推測するため。
だから、母集団と標本集団が異なる集団になってしまうことのないようにしなくてはならないです。できるだけ作為の無いように公平に抽出しなくてはなりません。
作為の無い(無作為)とは以下の特徴のことです。
- ランダム性(標本の要素が完全にランダム)
- 代表性(標本が、調査対象者全体の結果に偏りがないか)
※機関のデータベースからデータを集めるのが有効
例えば、全国の高校三年生の学力を調査したいのに東大・京大へ進学する人の多い学生だけを抽出して「これが全国の高校生三年生の学力です」とすると奇妙であることがわかると思います。
再度強調しておきます!
データを取り統計量を計算する目的は母集団についての情報を得るためです。
標本集団の統計量から母集団を推測するには標本集団のデータの数がいりますね。
具体的に計算してみよう
ここでは平均を求める問題を解いてみましょう。
ただ、製品Aの重量にはばらつきが当然あるわけですが、今まで作製した製品Aをすべて洗い出して調査するわけにはいかないですよね。
なので20個を抽出してみると・・・・(単位kg)
これが標本集団ですね。
でした。
ここから平均を計算してみましょう!
平均&=\frac{24.5+ 15.5+ 22.5+ 26.5+ 23.5+ 28.0+ 27.5+ 29.0+ 30.0+ 19.5+ 23.0+ 20.5+ 6.5+ 22.5+ 27.0+ 20.5+ 32.5+ 14.5+ 22.0+ 22.0}{20}\\
&=22.875
\end{align*}
結果は「平均22.875kg」でした。
だから、「20kgより重い製品だ!」と結論づけて良いのでしょうか?
平均大きいけど20kgより小さいものもありますし、標本の統計量だけでは母集団を表しているかどうかがわからないですよね。
質量が「22.875kgkg」・・・これはこの工場の全製品Aの平均質量と言ってよいだろうか・・・もっとサンプル数を増やす必要があるのではないか?
標本集団からは統計量が得ることができたけど、これをどうやって母集団の特徴の理解に使おうか?
ここが統計学の腕の見せ所というわけですね。
まとめ
本記事では母集団と標本集団の違いについて解説しました。
また、なぜ標本集団から統計量を計算するのかというと・・・・
統計量を計算する目的は母集団の特徴を推測するため
統計量は標本集団から求まり、統計量を計算する目的は母集団の特徴を推測するため。
お勧めの統計学の参考書
統計解析の入門書として以下の3冊を挙げておきます。
↓こちらの参考書は統計学の使い方を丁寧に解説している良書です。統計学の数学の複雑な式が少なく、「統計的手法の手順」がよくまとまっているため実践にも使える内容です。
統計学は全くの初めてという方にはマセマの参考書をお勧めします。
式変形は丁寧ですし語り口調が専門書っぽくなく口語的で難しさを感じさせない工夫がされています。
↓こちらは統計学の数学的な内容も書かれている入門書です。