こんにちは(@t_kun_kamakiri)(^^)/
前回では「3次と4次の正方行列を余因子展開を使って計算する方法」についての内容をまとめました。
行列式の定義に従って計算するとかなり大変だったと思います。
今回は行列式を計算するうえでとても重要な公式を解説します。
$n$行$n$列の正方行列$A$に対して
- $k$行と$l$行が等しいければ行列式$|A|$は0である。
- $k$列と$l$列が等しいければ行列式$|A|$は0である。
この内容な何が重要でどういった嬉しさがあるのかは本記事を読んでいただければ理解できるでしょう!
これから線形代数を学ぶ学生や社会人のために「役に立つ内容にしたい」という思いで記事を書いていこうと考えています。
- 行列をはじめて習う高校生・大学生
- 仕事で行列を使うけど忘れてしまった社会人
この記事の内容をマスターして行列計算を楽に計算できるようになりましょう(^^)
行列式の重要な性質
行列式の計算の計算をしやすくするための重要な性質があります。
行方向で言えることは列方向でもいえるということです。
言葉ではわかりにくいので行列式を書いてみました。
$k$行と$l$行が等しいければ行列式$|A|$は0である。

$k$列と$l$列が等しいければ行列式$|A|$は0である。
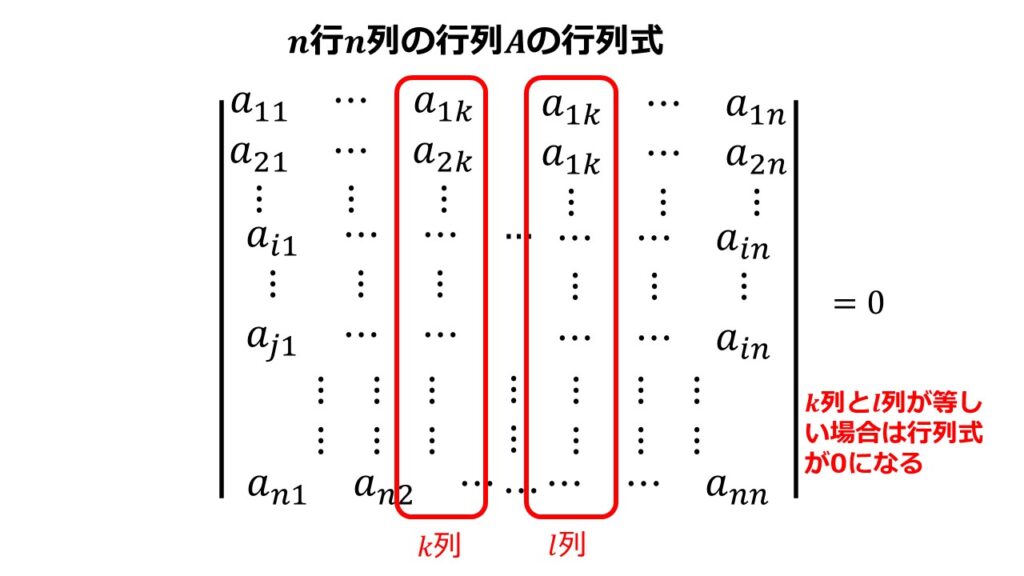
これは行列式の計算を楽にするためのとても重要な性質なので絶対に覚えておきましょう!
証明
では、本当に「等しい行、等しい列」があった場合に行列式が0になるのかのを証明を示します。
ここでは等しい行がある場合のみ証明を行います。
証明には行列式の定義から計算するため、下記の「置換の定義」を理解しておく必要があります。
$n$行$n$列の正方行列Aについて、行列式を以下のように定義する。
|A|&=\sum sgn\,\begin{pmatrix}
1 &2 &\cdots&k &\cdots& l&\cdots &n \\
i_{1} &i_{2} &\cdots&i_{k} &\cdots&i_{k}&\cdots &i_{n}
\end{pmatrix} \cdot a_{1\sigma_{1}}a_{2\sigma_{2}}\cdots a_{n\sigma_{n}}\tag{1}
\end{align*}
置換の符号は下の行の入れ替え回数が偶数回なら+(プラス)符号を、奇数回ー(マイナス)になるので、$i_{k}$と$i_{l}$を入れ替えると符号が変わります。
&sgn\,\begin{pmatrix}
1 &2 &\cdots&k &\cdots& l&\cdots &n \\
i_{1} &i_{2} &\cdots&i_{k} &\cdots&i_{l}&\cdots &i_{n}\end{pmatrix}\\
&=-sgn\,\begin{pmatrix}
1 &2 &\cdots&k &\cdots& l&\cdots &n \\
i_{1} &i_{2} &\cdots&i_{l} &\cdots&i_{k}&\cdots &i_{n}
\end{pmatrix}
\end{align*}
この性質を使うと行列$A$は以下のように書けます。
|A|&=\sum sgn\,\begin{pmatrix}
1 &2 &\cdots&k &\cdots& l&\cdots &n \\
i_{1} &i_{2} &\cdots&i_{k} &\cdots&i_{l}&\cdots &i_{n}\end{pmatrix} \cdot a_{1\sigma_{1}}a_{2\sigma_{2}}\cdots a_{k\sigma_{k}}\cdots a_{l\sigma_{l}}&\cdots a_{n\sigma_{n}}\\
&=-\sum sgn\,\begin{pmatrix}
1 &2 &\cdots&k &\cdots& l&\cdots &n \\
i_{1} &i_{2} &\cdots&i_{l} &\cdots&i_{k}\cdots &i_{n}
\end{pmatrix} \cdot a_{1\sigma_{1}}a_{2\sigma_{2}}\cdots a_{k\sigma_{k}}\cdots a_{l\sigma_{l}}\cdots a_{n\sigma_{n}}
\end{align*}
ここで$k$行と$l$行が同じであるとき、
|A|&=\sum sgn\,\begin{pmatrix}
1 &2 &\cdots&k &\cdots& l&\cdots &n \\
i_{1} &i_{2} &\cdots&i_{k} &\cdots&i_{k}&\cdots &i_{n}\end{pmatrix} \cdot a_{1\sigma_{1}}a_{2\sigma_{2}}\cdots a_{k\sigma_{k}}\cdots a_{k\sigma_{k}} \cdots a_{n\sigma_{n}}\\
&=-\sum sgn\,\begin{pmatrix}
1 &2 &\cdots&k &\cdots& l&\cdots &n \\
i_{1} &i_{2} &\cdots&i_{k} &\cdots&i_{k}&\cdots &i_{n}
\end{pmatrix} \cdot a_{1\sigma_{1}}a_{2\sigma_{2}}\cdots a_{k\sigma_{k}}\cdots a_{k\sigma_{k}} \cdots a_{n\sigma_{n}}\\
&=-|A|\tag{2}
\end{align*}
となるため$|A|=0$となります。
今回の証明は行に対して行いましたが、列方向に対しても同様の流れで$|A|=0$の証明を行うことができます。
繰り返しになりますが、「等しい行、等しい列」があった場合に行列式が0になるというのが覚えておきたい結果です。
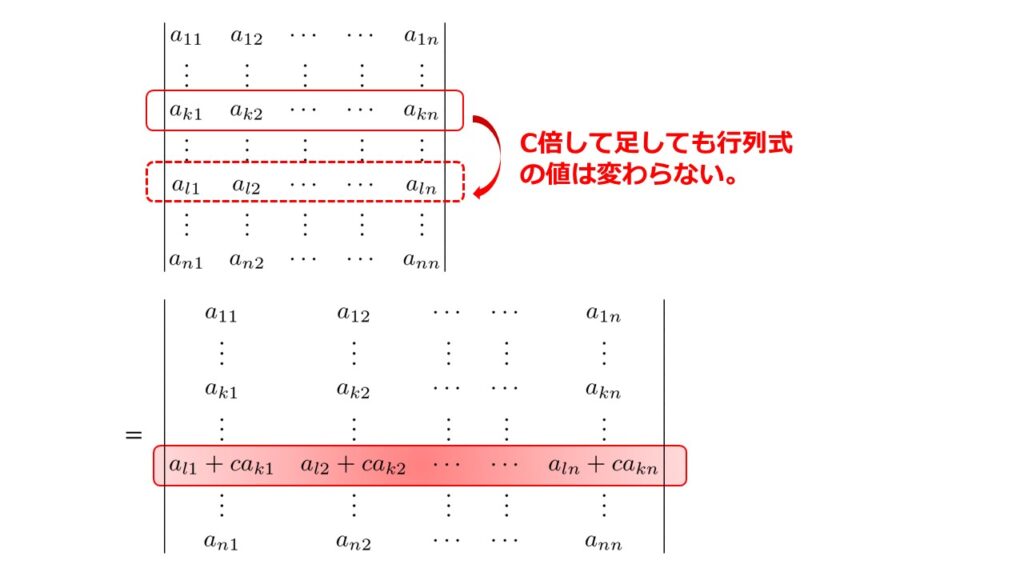
行列式に行or列に$c$倍足しても結果は同じ
「等しい行、等しい列」があった場合に行列式が0になるという結果は思いの他役に立つ性質です。
どういうことかと言うと、等しい行があった場合に行列式が0になるのであれば、適当なある行に定数$c$倍して別の行に足しても結果は変わらないため以下のように計算ができるわけです。
&\begin{vmatrix}
a_{11}& a_{12}& \cdots & \cdots &a_{1n} \\
\vdots&\vdots &\vdots & \vdots &\vdots \\
a_{k1}&a_{k2} & \cdots & \cdots& a_{kn}\\
\vdots& \vdots & \vdots &\vdots &\vdots \\
a_{l1}&a_{l2} & \cdots & \cdots & a_{ln}\\
\vdots &\vdots & \vdots& \vdots & \vdots\\
a_{n1}&a_{n2} & \cdots & \cdots &a_{nn} \\
\end{vmatrix}\\
&=
\begin{vmatrix}
a_{11}& a_{12}& \cdots & \cdots &a_{1n} \\
\vdots&\vdots &\vdots & \vdots &\vdots \\
a_{k1}&a_{k2} & \cdots & \cdots& a_{kn}\\
\vdots& \vdots & \vdots &\vdots &\vdots \\
a_{l1}&a_{l2} & \cdots & \cdots & a_{ln}\\
\vdots &\vdots & \vdots& \vdots & \vdots\\
a_{n1}&a_{n2} & \cdots & \cdots &a_{nn} \\
\end{vmatrix}+c\underset{i行とj行が等しいので0}{\begin{vmatrix}
a_{11}& a_{12}& \cdots & \cdots &a_{1n} \\
\vdots&\vdots &\vdots & \vdots &\vdots \\
a_{k1}&a_{k2} & \cdots & \cdots& a_{kn}\\
\vdots& \vdots & \vdots &\vdots &\vdots \\
a_{k1}&a_{k2} & \cdots & \cdots & a_{kn}\\
\vdots &\vdots & \vdots& \vdots & \vdots\\
a_{n1}&a_{n2} & \cdots & \cdots &a_{nn} \\
\end{vmatrix}}\\
&=\begin{vmatrix}
a_{11}& a_{12}& \cdots & \cdots &a_{1n} \\
\vdots&\vdots &\vdots & \vdots &\vdots \\
a_{k1}&a_{k2} & \cdots & \cdots& a_{kn}\\
\vdots& \vdots & \vdots &\vdots &\vdots \\
a_{l1}+ca_{k1}&a_{l2}+ca_{k2} & \cdots & \cdots & a_{ln}+ca_{kn}\\
\vdots &\vdots & \vdots& \vdots & \vdots\\
a_{n1}&a_{n2} & \cdots & \cdots &a_{nn} \\
\end{vmatrix}\tag{3}
\end{align*}
(3)の結果は非常に強力です!
行列式の数字を自由$c$倍して足したり(引いたり)しても結果が変わらないのであれば、計算しやすい形に行列式をどんどん変えていくことができるということです。
この性質がどれだけ強力な武器になるのかは以下の例題演習でおわかりいただけるでしょう。
例題演習
3次正方行列の行列式はサラスの公式を用いれば求まりますが、例題のような4次以上の行列に対して行列式を求めるのはかなりハードルが上がるというのを前回の記事でも解説しました。
行列式の定義から計算するのは手計算においては少々厳しいので、余因子展開で求めるか本記事で紹介した行列式の性質を利用するかが通常の方法だと考えてください。
まずは余因子展開で求める方法を紹介します。
余因子展開で求める
余因子展開の場合はどの行に対して(もしくはどの列に対して)展開しても良いので今回は1列目に対して余因子展開を行います。
わかりやすくするために以下のように隠しながら式余因子展開を行うといいですね。
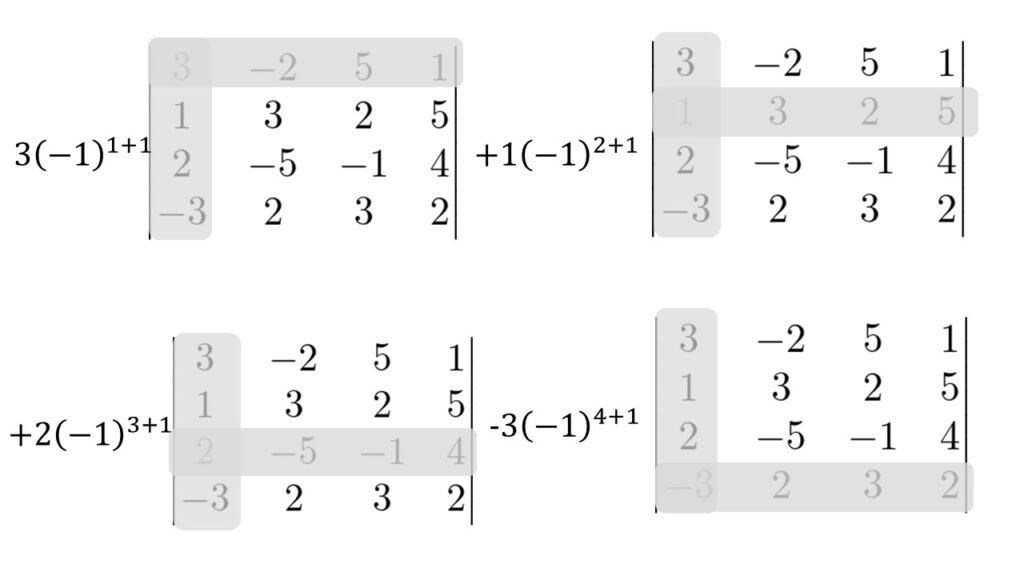
実際に書いていくと・・・
&\begin{vmatrix}
3 & -2 & 5 &1 \\
1 & 3 & 2 & 5 \\
2 & -5 & -1 & 4 \\
-3 & 2 & 3 & 2
\end{vmatrix}\\
&=3(-1)^{1+1}\begin{vmatrix}
3 & 2 & 5 \\
-5 & -1 & 4 \\
2 & 3 & 2
\end{vmatrix}
+1(-1)^{2+1}\begin{vmatrix}
-2 & 5 & 1 \\
2 & -1 & 4 \\
-3 & 3 & 2
\end{vmatrix}\\
&+2(-1)^{3+1}\begin{vmatrix}
-2 & 5 & 1 \\
3 & -1 & 4 \\
2 & 3 & 2
\end{vmatrix}
+(-3)(-1)^{4+1}\begin{vmatrix}\\
-2 & 5 & 1 \\
3 & 2 & 5 \\
-5 & -1 & 4
\end{vmatrix}\\
&=3\times (-71)-\times 105 +2\times (47)-(-3)\times (-204)\\
&=-863\tag{4}
\end{align*}
本記事の内容:行列式の性質を使う
余因子展開を使った計算も簡単で使いやすいですが行列式を計算するときは、本記事の内容で紹介した行列式の性質(定数倍したものを別の行か列に足しても行列式は変化しない)を使った方が楽な場合が多いです。
ポイントはどこの行や列を使っていかに0を作っていくかです。
例えば今回の場合は、「2行1列に1があるのでこれを使って1列目は0が作れるな~」と考えて計算を進めていきます。
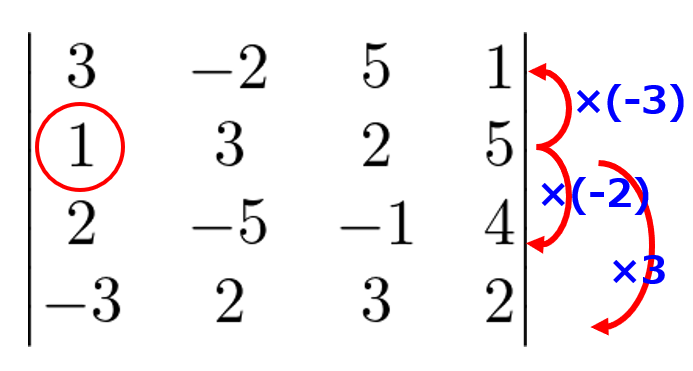
↑計算の第一歩はこれ
\begin{vmatrix}
3 & -2 & 5 &1 \\
1 & 3 & 2 & 5 \\
2 & -5 & -1 & 4 \\
-3 & 2 & 3 & 2
\end{vmatrix}&=\underset{2行目を定数倍して2行目以外に足す}{\begin{vmatrix}
0 & -11 & -1 &-14 \\
1 & 3 & 2 & 5 \\
0 & -11 & -5 & -6 \\
0 & 11 & 9 & 17
\end{vmatrix}}\\
&=\underset{2行目と1行目を入れ替える\\※-1倍する}{(-1)\begin{vmatrix}
1 & 3 & 2 & 5 \\
0 & -11 & -1 &-14 \\
0 & -11 & -5 & -6 \\
0 & 11 & 9 & 17
\end{vmatrix}}\\
&=\underset{1列目で余因子展開する}{(-1)\begin{vmatrix}
-11 & -1 &-14 \\
-11 & -5 & -6 \\
11 & 9 & 17
\end{vmatrix}}\\
&=\underset{1行目と2行目を-1倍する}{(-1)(-1)(-1)\begin{vmatrix}
11 & 1 &14 \\
11 & 5 & 6 \\
11 & 9 & 17
\end{vmatrix}}\\
&=\underset{1列目の11を外に出す}{(-1)(-1)(-1)11\begin{vmatrix}
1 & -1 &-14 \\
1 & -5 & 6 \\
1 & 9 & 17
\end{vmatrix}}\\
&=\underset{1行目の定数倍を2,3行目に足す}{(-1)(-1)(-1)11\begin{vmatrix}
1 & -1 &-14 \\
0 & 4 & -8 \\
0 & 8 & 3
\end{vmatrix}}\\
&=\underset{2行2列の行列式は簡単}{-11\times (4\times 3 – (-8)\times 8)}\\
&=-836\tag{5}
\end{align*}
このように計算しやすいように適当な行に定数倍したものを別の行に足していけばどんどん式が簡単になります。3行3列の行列式にできた時点でサラスの公式を使っても良いですし、今回のように2行2列まで式を簡単にしても良いです。
まとめ
今回の記事では行列式の重要な性質を解説しました。
行列式を簡単にするための重要な性質なので必ずマスターしておきましょう(^^)/
参考にする参考書はこれ
当ブログでは、以下の2つの参考書を読みながらよく使う内容をかいつまんで、一通り勉強すればついていけるような内容を目指していこうと思います。
大事なところをかいつまんで、「これはよく使うよな。これを理解するためには補足で説明をする」という調子で進めていきます(^^)/