【基底変換】基底の変換行列をわかりやすく解説

前回の記事では固有ベクトル$\boldsymbol{x}_{1}$,$\boldsymbol{x}_{2}$を基底に取るような線形空間を考えると行列$A$が対角行列になることを示しました。

前回の記事

今回の記事は基底変換について解説を行います。
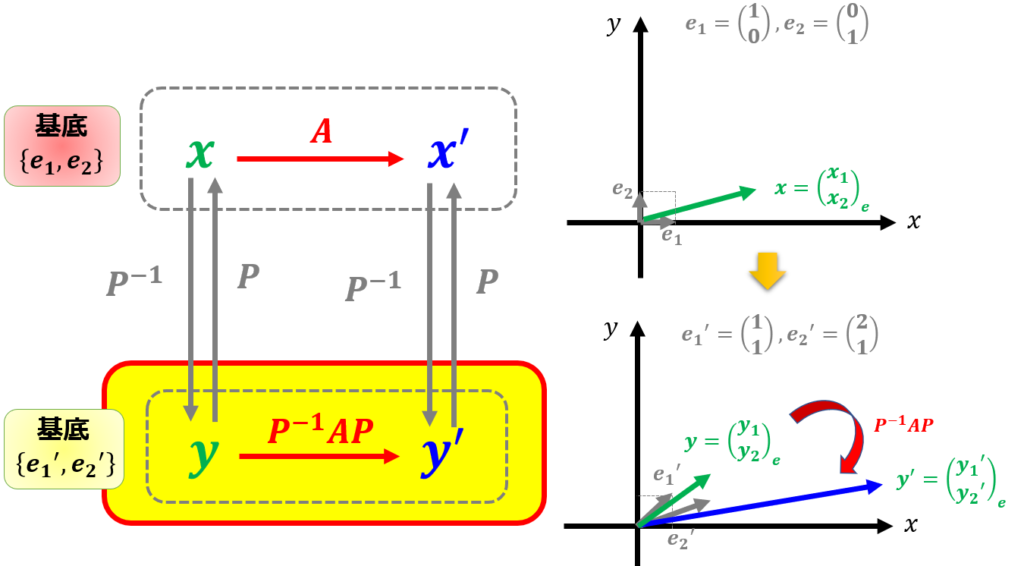
「ある基底$\{e_{1},e_{2}\}$での線形変換$A$は別の基底$\{e^{\prime}_{1},e^{\prime}_{2}\}$でどのように表されるのか」というのを示します。

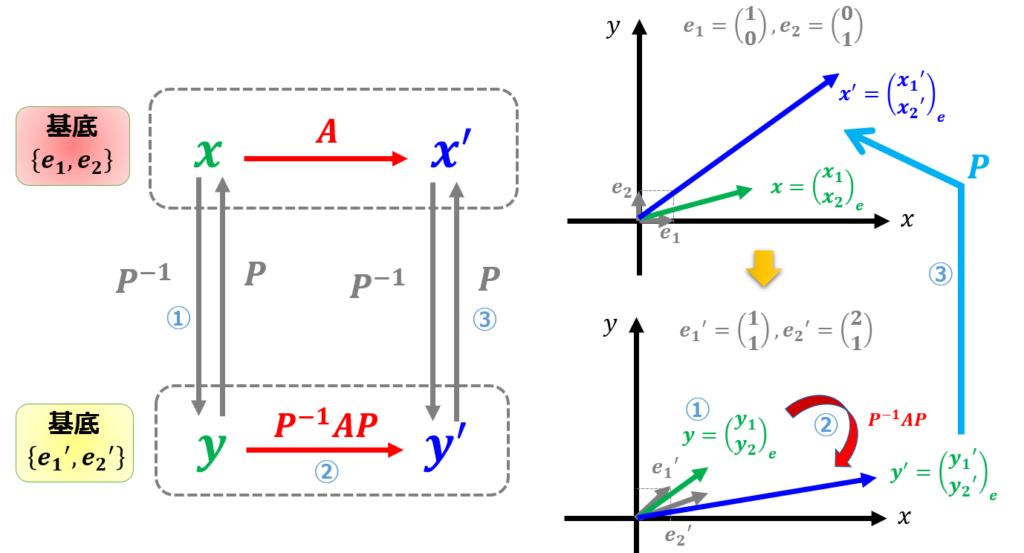
これが本記事の主題となります。

本記事の内容

ある基底変換により線形変換行列$A$を、別の基底に対応する線形変換行列は$P^{-1}AP$となることを示す

これから線形代数を学ぶ学生や社会人のために「役に立つ内容にしたい」という思いで記事を書いていこうと考えています。

こんな人が対象

行列をはじめて習う高校生・大学生
仕事で行列を使うけど忘れてしまった社会人

この記事の内容をマスターして基底変換に関しての理解を深めましょう(^^)

線形変換について
線形変換は基底を変えずに成分を変換
1. 具体的な計算
2. 任意の2次元ベクトルの変換
別の基底で$\boldsymbol{x}$を書く
基底変換する変換行列
別の基底での対応する線形変換$P^{-1}AP$
元の基底に戻す$\boldsymbol{x}^{\prime}=P\boldsymbol{y}^{\prime}$
$n$次元に拡張できる
まとめ
参考にする参考書はこれ

線形変換について

なずは、線形変換の定義について触れておきます。

線形変換の定義

$K$上の線形空間$V$から$K$上の線形空間$V^{\prime}$への写像$f$が以下の2条件を満たすとき$f$を$V$から$V^{\prime}$への線形写像と言います。

$f(\boldsymbol{x}+\boldsymbol{y})=f(\boldsymbol{x})+f(\boldsymbol{y})$
$f(a\boldsymbol{x})=aT(\boldsymbol{x})$

特に$V$から$V$自身への線形写像を$V$の線形変換と言う.

カマキリ

何書いているかわからないですよね。

$K$上とは実数全体の集合$R$と複素数全体の集合$C$を統一して表しています。
なので、「$K$上の線形空間$V$」と書くと「複素線形空間、実数線形空間」を意味しています。わかりやすい言葉で言うと「実数・複素数のベクトルの集合」ということです。

次に、$f(\boldsymbol{x})$は何か$f$というフィルターを通すと出てくる装置みたいなものです。具体的には行列$A$を$\boldsymbol{x}$に作用させると$A\boldsymbol{x}$という変換が行われるわけです。

$V$の次元を$n$とする。$V$の1つの基底を$\{\boldsymbol{e}_{1},\boldsymbol{e}_{1},\cdots,\boldsymbol{e}_{n}\}$とすると、$V$の任意の元は以下のように基底の線型結合で表すことができる。

\begin{align*}
\boldsymbol{x}&=\begin{pmatrix}
c_1\\
c_2\\
\vdots\\
c_n
\end{pmatrix}\\
&=c_1\begin{pmatrix}
1\\
0\\
\vdots\\
0
\end{pmatrix}+c_2\begin{pmatrix}
0\\
1\\
\vdots\\
0
\end{pmatrix}+\cdots+c_n\begin{pmatrix}
0\\
0\\
\vdots\\
1
\end{pmatrix}\\
&=c_1\boldsymbol{e}_{1}+c_2\boldsymbol{e}_{2}\cdots +c_n\boldsymbol{e}_{n}\\
&=\sum_{i=1}^{n}c_{i}\boldsymbol{e}_{i}
\end{align*}

線形変換は基底を変えずに成分を変換

まずは図を使って解説をするために線形空間$V$を2次元で考えることにします。

特に断りがない限り、基底を$x$軸方向の単位ベクトル$\boldsymbol{e}_{1}=\begin{pmatrix}
1\\
0\\
\end{pmatrix}$と$y$軸方向の単位ベクトル$\boldsymbol{e}_{2}=\begin{pmatrix}
0\\
1\\
\end{pmatrix}$に取ることが多いので、線形独立はベクトル$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$を基底とします。

まずは具体的な計算をすることで、何が起こっているのかを把握することから始めましょう。

具体的な計算

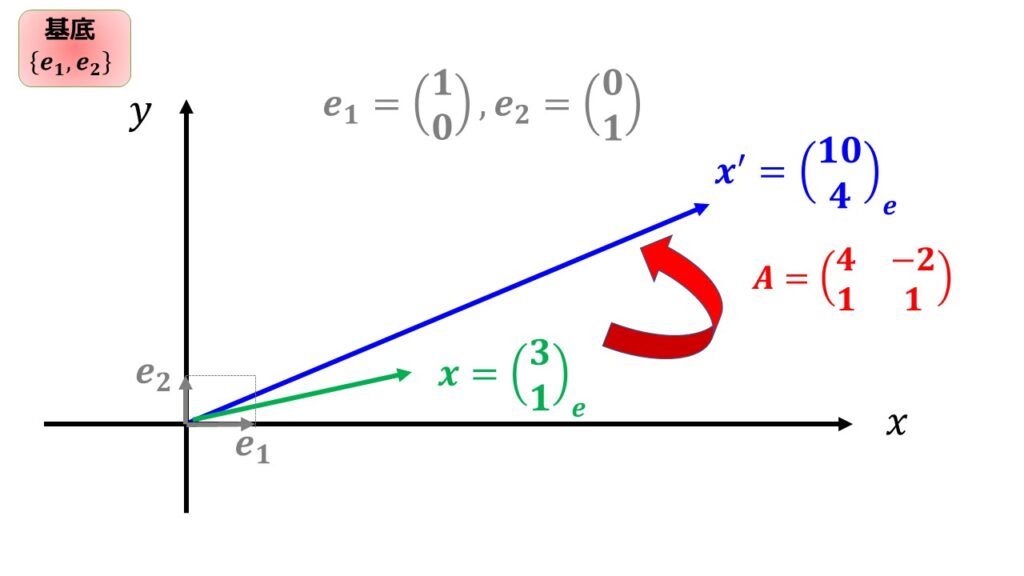
今、$\boldsymbol{x}=\begin{pmatrix}
3\\
1\\
\end{pmatrix}$のベクトルを線形変換する行列$A=\begin{pmatrix}
4 & -2\\
1 & 1
\end{pmatrix}$で変換することを考えます。
結果は$\boldsymbol{x^{\prime}}=\begin{pmatrix}
4 & -2\\
1 & 1
\end{pmatrix}\begin{pmatrix}
3\\
1\\
\end{pmatrix}=\begin{pmatrix}
10\\
4
\end{pmatrix}$と計算ができます。

これを図にすると以下のようになります。

行列の掛け算の計算が面倒ですが、$\boldsymbol{x}$が行列$A$を使って$\boldsymbol{x^{\prime}}$に変換されたのがわかります。ただ普通に行列計算をしただけですが、変換された$\boldsymbol{x^{\prime}}=\begin{pmatrix}
10\\
4\\
\end{pmatrix}$は基底が相変わらず$\boldsymbol{e}_{1}=\begin{pmatrix}
1\\
0\\
\end{pmatrix}$と$\boldsymbol{e}_{2}=\begin{pmatrix}
0\\
1\\
\end{pmatrix}$であることに注意です。

つまり、基底が$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$のまま線形変換$A$によって$\boldsymbol{x^{\prime}}=\begin{pmatrix}
10\\
4
\end{pmatrix}$になったということです。

ここで言いたいのは、基底が変わらず成分の値だけが変わったということです。

では、今度は具体的な数字を使わずに表現してみましょう。

任意の2次元ベクトルの変換

任意の2次元ベクトル$\boldsymbol{x}=\begin{pmatrix}
x_{1}\\
x_{2}\\
\end{pmatrix}$を考えます。

これは

\begin{align*}
\boldsymbol{x}&=x_1\begin{pmatrix}
1\\
0
\end{pmatrix}+x_2\begin{pmatrix}
0\\
1
\end{pmatrix}\\
&=x_{1}\boldsymbol{e}_{1}+x_{2}\boldsymbol{e}_{2}\\
&=\sum_{i=1}^{2}x_{i}\boldsymbol{e}_{i}\tag{1}
\end{align*}

とも書けますね。
このように書くと、どの基底を使ったときの表現なのか迷子になりそうなので、以下のように書きます。

$\boldsymbol{x}=\begin{pmatrix}
x_{1}\\
x_{2}\\
\end{pmatrix}_{e}$：右下に添え字で基底を表記
$\boldsymbol{x}=\underset{基底がわかる\\ように列ベクトル\\で書く}{\begin{pmatrix}
\boldsymbol{e}_{1}&
\boldsymbol{e}_{2}
\end{pmatrix}}\begin{pmatrix}
x_{1}\\
x_{2}\\
\end{pmatrix}$

②のように書いておくとすごくわかりやすいですね
$\boldsymbol{x}=\begin{pmatrix}
x_{1}\\
x_{2}\\
\end{pmatrix}$ではなく、$\boldsymbol{x}=\begin{pmatrix}
\boldsymbol{e}_{1}&
\boldsymbol{e}_{2}
\end{pmatrix}\begin{pmatrix}
x_{1}\\
x_{2}\\
\end{pmatrix}=\begin{pmatrix}
1&0\\
0&1\end{pmatrix}\begin{pmatrix}
x_{1}\\
x_{2}\\
\end{pmatrix}=x_1\begin{pmatrix}
1\\
0
\end{pmatrix}+x_2\begin{pmatrix}
0\\
1
\end{pmatrix}$のように、基底を前に書いておく方がわかりやすいのですよね。
ちなみに$\begin{pmatrix}
\boldsymbol{e}_{1}&
\boldsymbol{e}_{2}
\end{pmatrix}=\begin{pmatrix}
1&0\\
0&1\end{pmatrix}=E$(単位行列)です。

②を使って行列$A=\begin{pmatrix}
a_{11}&a_{12}\\
a_{21}&a_{22}\end{pmatrix}$による変換を行うと、

\begin{align*}
A\boldsymbol{x}&=\begin{pmatrix}
a_{11}&a_{12}\\
a_{21}&a_{22}\end{pmatrix}
\begin{pmatrix}
x_{1}\\
x_{2}\\
\end{pmatrix}\\
&=\begin{pmatrix}
a_{11}&a_{12}\\
a_{21}&a_{22}\end{pmatrix}
\underset{単位行列E}{\begin{pmatrix}
\boldsymbol{e}_{1}&
\boldsymbol{e}_{2}
\end{pmatrix}}
\begin{pmatrix}
x_{1}\\
x_{2}
\end{pmatrix}\\
&=\begin{pmatrix}
\boldsymbol{e}_{1}&
\boldsymbol{e}_{2}
\end{pmatrix}\begin{pmatrix}
a_{11}&a_{12}\\
a_{21}&a_{22}\end{pmatrix}
\begin{pmatrix}
x_{1}\\
x_{2}\\
\end{pmatrix}\\
&=\begin{pmatrix}
\boldsymbol{e}_{1}&
\boldsymbol{e}_{2}
\end{pmatrix}\begin{pmatrix}
a_{11}x_{1}+a_{12}x_{2}\\
a_{21}x_{1}+a_{22}x_{2}\end{pmatrix}\\
&=\boldsymbol{x^{\prime}}\tag{2}
\end{align*}

となります。
このように書くと基底を$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$から変えずに成分だけが変わっているのがよくわかりますね。

つまり以下のようになっているということです。

\begin{align*}
A\boldsymbol{x}&=\boldsymbol{x}^{\prime}\\
&=\begin{pmatrix}
\boldsymbol{e}_{1}&
\boldsymbol{e}_{2}
\end{pmatrix}\begin{pmatrix}
x_{1}^{\prime}\\
x_{2}^{\prime}
\end{pmatrix}\\
&=x_{1}^{\prime}\boldsymbol{e}_{1}+x_{2}^{\prime}\boldsymbol{e}_{2}\\
&=\sum_{i=1}^{2}x_{i}^{\prime}\boldsymbol{e}_{i}\tag{4}
\end{align*}

$x_{1}^{\prime}=a_{11}x_{1}+a_{12}x_{2}$
$x_{2}^{\prime}=a_{21}x_{1}+a_{22}x_{2}$

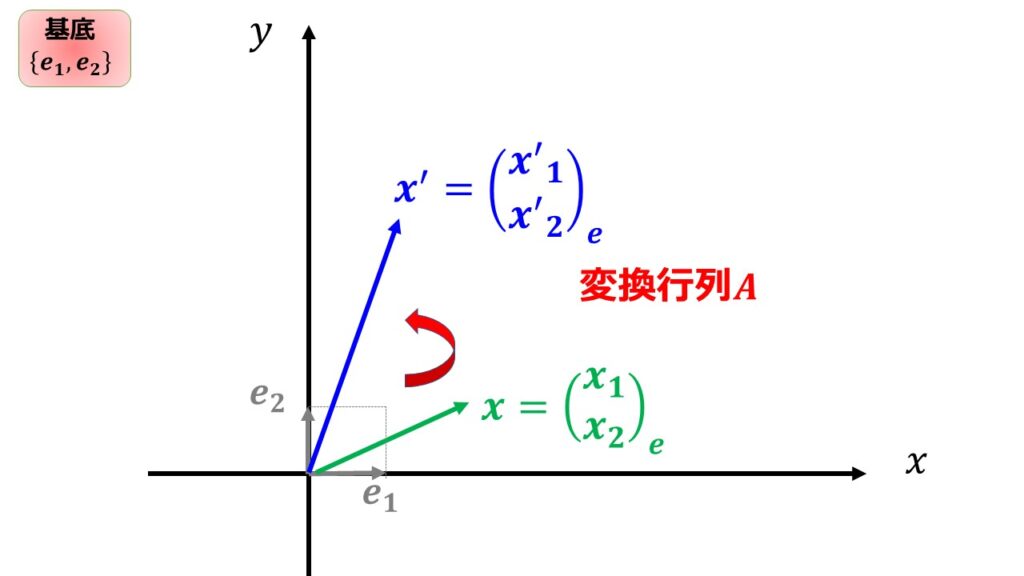
何度も繰り返しますが、ここで大事なのは線形変換$A$によって基底を変えずに成分だけを変換したということです。

別の基底で$\boldsymbol{x}$を書く

基底が$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$であるときの$\boldsymbol{x}$を別の基底$\{\boldsymbol{e}_{1}^{\prime},\boldsymbol{e}_{2}^{\prime}\}$で書くことにします。

\begin{align*}
\boldsymbol{x}&=x_{1}\boldsymbol{e}_{1}+x_{2}\boldsymbol{e}_{2}=\begin{pmatrix}
\boldsymbol{e}_{1} &\boldsymbol{e}_{2}\end{pmatrix}
\begin{pmatrix}
x_{1}\\
x_{2}
\end{pmatrix}\\
&=y_{1}\boldsymbol{e}^{\prime}_{1}+y_{2}\boldsymbol{e}^{\prime}_{2}=\begin{pmatrix}
\boldsymbol{e}^{\prime}_{1} &\boldsymbol{e}^{\prime}_{2}\end{pmatrix}
\begin{pmatrix}
y_{1}\\
y_{2}
\end{pmatrix}
\end{align*}

となります。

基底変換する変換行列

今までは基底が$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$であったから線形変換$A=\begin{pmatrix}
a_{11}&a_{12}\\
a_{21}&a_{22}\end{pmatrix}$でしたが、これを基底を変換する行列$P$を導入すると、新たな基底が$\{\boldsymbol{e}^{\prime}_{1},\boldsymbol{e}^{\prime}_{2}\}$では線形変換$A$はどのような変更を受けるのかを考えてみましょう。

この行列$P$を変換行列といいます。
行列$P$には逆行列$P^{-1}$が存在するとします。

計算式が長くなると迷子になりかねないので先に結論を述べておきましょう。

基底が$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$での線形変換$A$は、基底を変換する変換行列$P$を用いると、新たな基底$\{\boldsymbol{e}^{\prime}_{1},\boldsymbol{e}^{\prime}_{2}\}$で表したときの成分に対して対応する線形変換は$P^{-1}AP$となります。

基底は変換行列$P$で以下のように変換されます。

$\begin{pmatrix}
\boldsymbol{e}_{1}&\boldsymbol{e}_{2}
\end{pmatrix}=P^{-1}\begin{pmatrix}
\boldsymbol{e}^{\prime}_{1}&\boldsymbol{e}^{\prime}_{2}
\end{pmatrix}$
もしくは、
$\begin{pmatrix}
\boldsymbol{e}^{\prime}_{1}&\boldsymbol{e}^{\prime}_{2}
\end{pmatrix}=P\begin{pmatrix}
\boldsymbol{e}_{1}&\boldsymbol{e}_{2}
\end{pmatrix}$

具体的に書くと$\begin{pmatrix}
\boldsymbol{e}^{\prime}_{1}&\boldsymbol{e}^{\prime}_{2}
\end{pmatrix}=P\begin{pmatrix}
\boldsymbol{e}_{1}&\boldsymbol{e}_{2}
\end{pmatrix}$は$\begin{pmatrix}
0 & 2\\
1 & 1
\end{pmatrix}
=P\begin{pmatrix}
1 & 0\\
0 & 1
\end{pmatrix}$です。
$P$は次回出てくる固有ベクトルからなるというのがわかります。

詳しく解説をしましょう。

別の基底での対応する線形変換$P^{-1}AP$

ここでも絵を使って解説を行うため2次元での線形空間で考えます。

先ほど解説したように基底を$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$のまま線形変換$A$で変換すると以下のように、基底が変わらずに成分だけが変わります。

$\boldsymbol{x}^{\prime}=A\boldsymbol{x}$をあえて基底がわかりようにして書くと以下のようになります。

\begin{align*}
\begin{pmatrix}
\boldsymbol{e}_{1} &\boldsymbol{e}_{2}\end{pmatrix}\begin{pmatrix}
x^{\prime}_{1}\\
x^{\prime}_{2}
\end{pmatrix}=A\begin{pmatrix}
\boldsymbol{e}_{1} &\boldsymbol{e}_{2}\end{pmatrix}
\begin{pmatrix}
x_{1}\\
x_{2}
\end{pmatrix}\\
\begin{pmatrix}
\boldsymbol{e}_{1}^{\prime} &\boldsymbol{e}_{2}^{\prime}\end{pmatrix}\begin{pmatrix}
y^{\prime}_{1}\\
y^{\prime}_{2}
\end{pmatrix}=A\begin{pmatrix}
\boldsymbol{e}_{1}^{\prime} &\boldsymbol{e}_{2}^{\prime}\end{pmatrix}
\begin{pmatrix}
y_{1}\\
y_{2}
\end{pmatrix}
\tag{5}
\end{align*}

ここで2つ目の式は基底を変えます。(5)の2つの式は同じ式です。
基底を変えたことで成分も変わっていることに注意ですね。

$\begin{pmatrix}
\boldsymbol{e}^{\prime}_{1}&\boldsymbol{e}^{\prime}_{2}
\end{pmatrix}=P\begin{pmatrix}
\boldsymbol{e}_{1}&\boldsymbol{e}_{2}
\end{pmatrix}$であることを用いると、

\begin{align*}
P\underset{\boldsymbol{y}^{\prime}}{\begin{pmatrix}
\boldsymbol{e}_{1} &\boldsymbol{e}_{2}\end{pmatrix}\begin{pmatrix}
y^{\prime}_{1}\\
y^{\prime}_{2}
\end{pmatrix}}=
AP\underset{\boldsymbol{y}}{\begin{pmatrix}
\boldsymbol{e}_{1} &\boldsymbol{e}_{2}\end{pmatrix}\begin{pmatrix}
y_{1}\\
y_{2}
\end{pmatrix}}
\tag{6}
\end{align*}

両辺、左から$P^{-1}$を作用させると、

\begin{align*}
\underset{\boldsymbol{y}^{\prime}}{\begin{pmatrix}
\boldsymbol{e}_{1} &\boldsymbol{e}_{2}\end{pmatrix}\begin{pmatrix}
y^{\prime}_{1}\\
y^{\prime}_{2}
\end{pmatrix}}&=P^{-1}AP\underset{\boldsymbol{y}}{\begin{pmatrix}
\boldsymbol{e}_{1} &\boldsymbol{e}_{2}\end{pmatrix}
\begin{pmatrix}
y_{1}\\
y_{2}
\end{pmatrix}}\\
\boldsymbol{y}^{\prime}&=P^{-1}AP\boldsymbol{y}
\tag{7}
\end{align*}

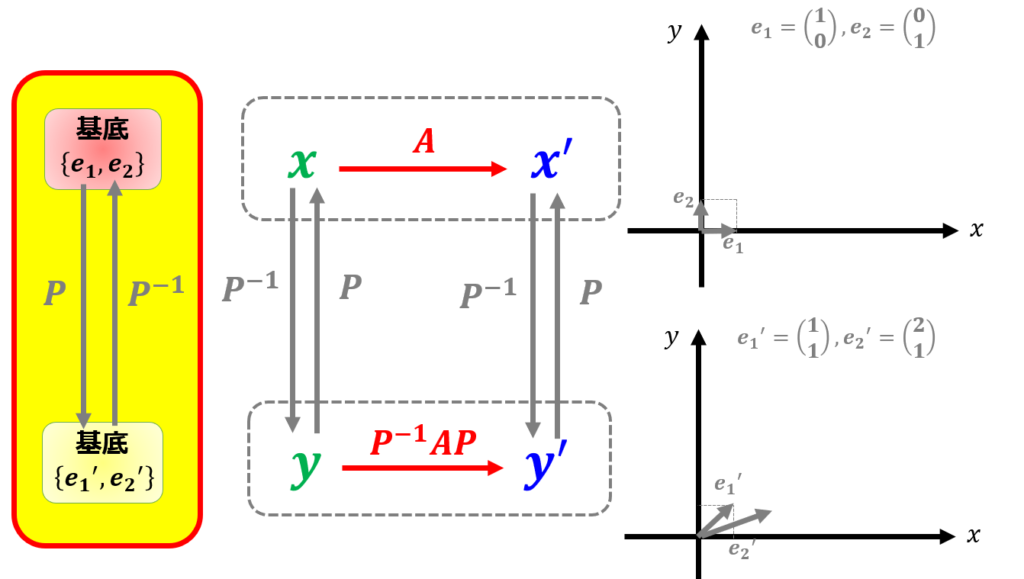
よって、基底$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$での線形変換$A$は別の基底$\{\boldsymbol{e}^{\prime}_{1},\boldsymbol{e}^{\prime}_{2}\}$で表したときの成分は、線形変換は基底の変換行列$P$を用いると$P^{-1}AP$となりました。

ここまでで何が行われたのかを丁寧に見ていきましょう。

まずは基底変換$\begin{pmatrix}
\boldsymbol{e}^{\prime}_{1}&\boldsymbol{e}^{\prime}_{2}
\end{pmatrix}=P\begin{pmatrix}
\boldsymbol{e}_{1}&\boldsymbol{e}_{2}
\end{pmatrix}$ですね。
これはある基底を別の基底に変換することを意味しています。

ここで注意する点としては、

\begin{align*}
\boldsymbol{x}&=x_{1}\boldsymbol{e}_{1}+x_{2}\boldsymbol{e}_{2}=\begin{pmatrix}
\boldsymbol{e}_{1} &\boldsymbol{e}_{2}\end{pmatrix}
\begin{pmatrix}
x_{1}\\
x_{2}
\end{pmatrix}\\
&=y_{1}\boldsymbol{e}^{\prime}_{1}+y_{2}\boldsymbol{e}^{\prime}_{2}=\begin{pmatrix}
\boldsymbol{e}^{\prime} &\boldsymbol{e}^{\prime}_{2}\end{pmatrix}
\begin{pmatrix}
y_{1}\\
y_{2}
\end{pmatrix}\tag{8}
\end{align*}

と、このように書いた場合はベクトル$\boldsymbol{x}$は変わっていないけど、基底を$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$から$\{\boldsymbol{e}^{\prime}_{1},\boldsymbol{e}^{\prime}_{2}\}$に変えたことで成分が変わっているということです。
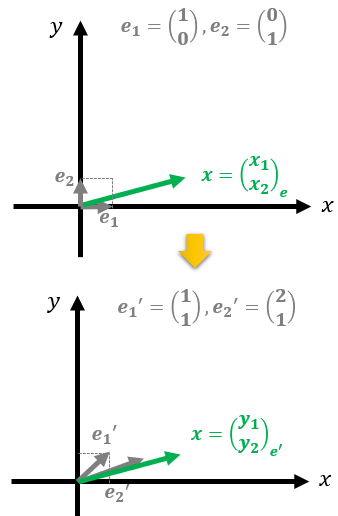
新たな基底を$\boldsymbol{e}^{\prime}_{1}=\begin{pmatrix}
1\\
1
\end{pmatrix},\boldsymbol{e}^{\prime}_{2}=\begin{pmatrix}
2\\
1
\end{pmatrix}$とします。

基底$\{\boldsymbol{e}_{1}^{\prime},\boldsymbol{e}_{2}^{\prime}\}$を右に絵のように垂直に取り直すと、成分が変わっているのでベクトルの方向も大きさも変わって見えています。しかし、基底$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$上に無理やり$\boldsymbol{x}=\begin{pmatrix}
y_{1}\\
y_{2}
\end{pmatrix}_{\boldsymbol{e}^{\prime}}$を書くのであれば$\boldsymbol{x}$であることには変わりないので、ベクトルの大きさと方向は変わりません。

$\boldsymbol{y}$は今、基底を$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$としたときの$\boldsymbol{y}=\begin{pmatrix}
\boldsymbol{e}_{1} &\boldsymbol{e}_{2}\end{pmatrix}
\begin{pmatrix}
y_{1}\\
y_{2}
\end{pmatrix}$に$\begin{pmatrix}
\boldsymbol{e}_{1}&\boldsymbol{e}_{2}
\end{pmatrix}=P^{-1}
\begin{pmatrix}
\boldsymbol{e}^{\prime}_{1}&\boldsymbol{e}^{\prime}_{2}
\end{pmatrix}$の関係を用いると、

\begin{align*}
\boldsymbol{y}&=P^{-1}
\begin{pmatrix}
\boldsymbol{e}^{\prime}_{1}&\boldsymbol{e}^{\prime}_{2}
\end{pmatrix}
\begin{pmatrix}
y_{1}\\
y_{2}
\end{pmatrix}\\
&=P^{-1}\boldsymbol{x}\tag{10}
\end{align*}

と書くことができます。

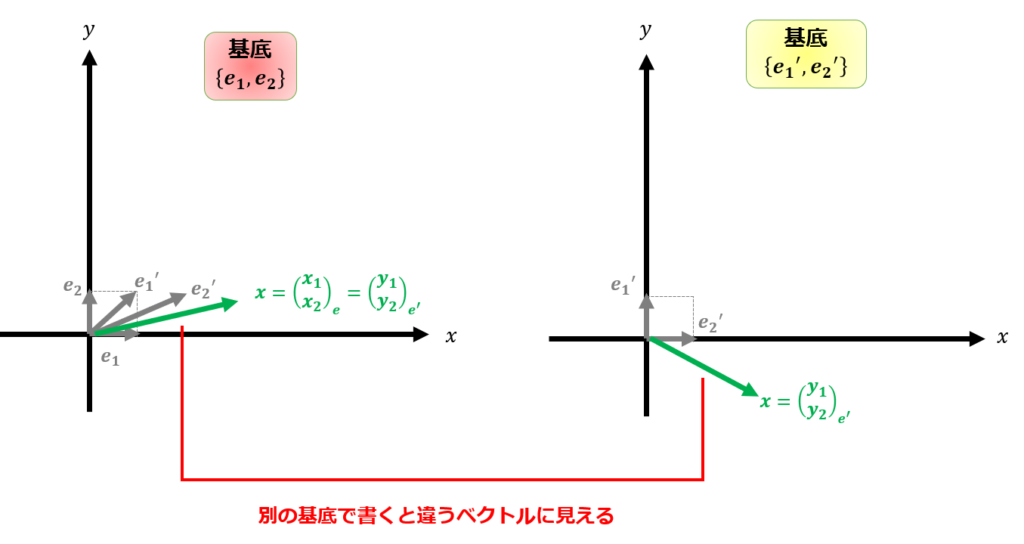
ややこしいですが、

基底$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$で書いた$\boldsymbol{y}=\begin{pmatrix}
\boldsymbol{e}_{1} &\boldsymbol{e}_{2}\end{pmatrix}
\begin{pmatrix}
y_{1}\\
y_{2}
\end{pmatrix}$
基底$\{\boldsymbol{e}_{1}^{\prime},\boldsymbol{e}_{2}^{\prime}\}$に書いた$\boldsymbol{x}=\begin{pmatrix}
\boldsymbol{e}_{1}^{\prime} &\boldsymbol{e}_{2}^{\prime}\end{pmatrix}
\begin{pmatrix}
y_{1}\\
y_{2}
\end{pmatrix}$

は異なるベクトルであることに注意です。

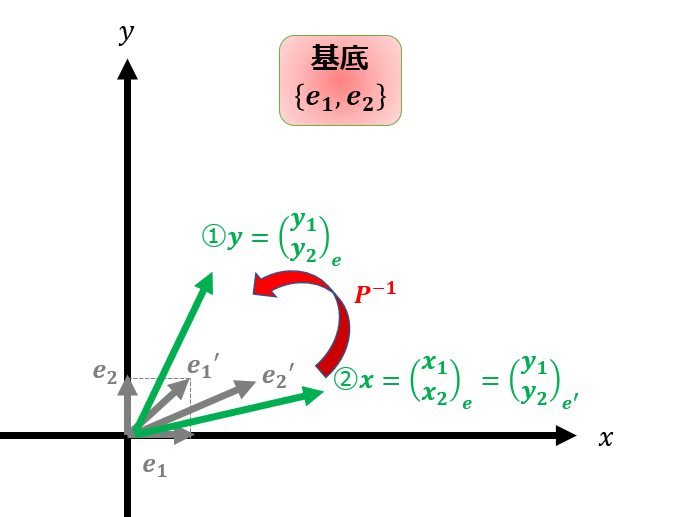
もう一度式を書いておきます。

基底変換の変換行列$P$を使って$\boldsymbol{y}=P^{-1}\boldsymbol{x}$とすることで、$\boldsymbol{y}$の成分に関しては線形変換が$P^{-1}AP$になったということです。

このようにして、以下のことが示せたということです。

基底は変換行列$P$で以下のように変換されます。

元の基底に戻す$\boldsymbol{x}^{\prime}=P\boldsymbol{y}^{\prime}$

いやいや、新たな基底$\{\boldsymbol{e}^{\prime}_{1},\boldsymbol{e}^{\prime}_{2}\}$の成分の線形変換の結果とか知りたくなくて、元の基底$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$での線形変換$A$の結果がほしいのですが・・・

カマキリ

当然の疑問かもしれません。

このような場合でも非常に簡単です。

基底の変換が$\begin{pmatrix}
\boldsymbol{e}_{1}&\boldsymbol{e}_{2}
\end{pmatrix}=P^{-1}\begin{pmatrix}
\boldsymbol{e}^{\prime}_{1}&\boldsymbol{e}^{\prime}_{2}
\end{pmatrix}$もしくは$\begin{pmatrix}
\boldsymbol{e}^{\prime}_{1}&\boldsymbol{e}^{\prime}_{2}
\end{pmatrix}=P\begin{pmatrix}
\boldsymbol{e}_{1}&\boldsymbol{e}_{2}
\end{pmatrix}$であることを用います。
(10)の基底変換$\boldsymbol{y}=P^{-1}\boldsymbol{x}$もしくは$\boldsymbol{x}=P\boldsymbol{y}$であったように、線形変換後も同様の関係が成り立つことを使のがよいですね。

基底が$\begin{pmatrix}
\boldsymbol{e}_{1} &\boldsymbol{e}_{2}\end{pmatrix}$であるときの$A$の変換に対応した$\begin{pmatrix}
\boldsymbol{e}_{1}^{\prime} &\boldsymbol{e}_{2}^{\prime}\end{pmatrix}$での変換は$P^{-1}AP$でした。
この変換により基底$\begin{pmatrix}
\boldsymbol{e}_{1}^{\prime} &\boldsymbol{e}_{2}^{\prime}\end{pmatrix}$では$\begin{pmatrix}
\boldsymbol{e}_{1}^{\prime} &\boldsymbol{e}_{2}^{\prime}\end{pmatrix}\begin{pmatrix}
y^{\prime}_{1}\\
y^{\prime}_{2}
\end{pmatrix}$に表されています。
※あえて基底がわかるように書いています。

これを、基底を元に戻して基底$\begin{pmatrix}\boldsymbol{e}_{1} &\boldsymbol{e}_{2}\end{pmatrix}$で考えたときにどうなるかを考えます。

$\begin{pmatrix}
\boldsymbol{e}_{1}^{\prime} &\boldsymbol{e}_{2}^{\prime}\end{pmatrix}
\begin{pmatrix}
y^{\prime}_{1}\\
y^{\prime}_{2}
\end{pmatrix}$を$\begin{pmatrix}\boldsymbol{e}_{1} &\boldsymbol{e}_{2}\end{pmatrix}$の基底で見た場合の成分を$\begin{pmatrix}
x^{\prime}_{1}\\
x^{\prime}_{2}
\end{pmatrix}$とするのであれば、$\begin{pmatrix}
\boldsymbol{e}_{1}^{\prime} &\boldsymbol{e}_{2}^{\prime}\end{pmatrix}
\begin{pmatrix}
y^{\prime}_{1}\\
y^{\prime}_{2}
\end{pmatrix}=\begin{pmatrix}
\boldsymbol{e}_{1} &\boldsymbol{e}_{2}\end{pmatrix}
\begin{pmatrix}
x^{\prime}_{1}\\
x^{\prime}_{2}
\end{pmatrix}=\boldsymbol{x}^{\prime}$と書くことができます。

基底$\begin{pmatrix}\boldsymbol{e}_{1} &\boldsymbol{e}_{2}\end{pmatrix}$で見たときの成分$\begin{pmatrix}
x^{\prime}_{1}\\
x^{\prime}_{2}
\end{pmatrix}$が知りたい。

ここで、$\begin{pmatrix}
\boldsymbol{e}_{1}&\boldsymbol{e}_{2}
\end{pmatrix}=P^{-1}\begin{pmatrix}
\boldsymbol{e}^{\prime}_{1}&\boldsymbol{e}^{\prime}_{2}
\end{pmatrix}$を使い$\begin{pmatrix}
\boldsymbol{e}_{1}^{\prime} &\boldsymbol{e}_{2}^{\prime}\end{pmatrix}
\begin{pmatrix}
y^{\prime}_{1}\\
y^{\prime}_{2}
\end{pmatrix}$を変形させながら以下のような関係式を得ることができます。

\begin{align*}
\begin{pmatrix}
\boldsymbol{e}_{1}^{\prime} &\boldsymbol{e}_{2}^{\prime}\end{pmatrix}
\begin{pmatrix}
y^{\prime}_{1}\\
y^{\prime}_{2}
\end{pmatrix}&=
P\begin{pmatrix}
\boldsymbol{e}_{1} &\boldsymbol{e}_{2}\end{pmatrix}\begin{pmatrix}
y^{\prime}_{1}\\
y^{\prime}_{2}
\end{pmatrix}\end{align*}

上式の基底が$\begin{pmatrix}
\boldsymbol{e}_{1} &\boldsymbol{e}_{2}\end{pmatrix}$になったところで、$\begin{pmatrix}
\boldsymbol{e}_{1} &\boldsymbol{e}_{2}\end{pmatrix}\begin{pmatrix}
x^{\prime}_{1}\\
x^{\prime}_{2}
\end{pmatrix}=\boldsymbol{x}^{\prime}$であるので、

\begin{align*}
\underset{\boldsymbol{x}^{\prime}=\begin{pmatrix}
\boldsymbol{e}_{1} &\boldsymbol{e}_{2}\end{pmatrix}\begin{pmatrix}
x^{\prime}_{1}\\
x^{\prime}_{2}
\end{pmatrix}}{\begin{pmatrix}
\boldsymbol{e}_{1}^{\prime} &\boldsymbol{e}_{2}^{\prime}\end{pmatrix}
\begin{pmatrix}
y^{\prime}_{1}\\
y^{\prime}_{2}
\end{pmatrix}}&=
P\underset{\boldsymbol{y}^{\prime}}{\begin{pmatrix}
\boldsymbol{e}_{1} &\boldsymbol{e}_{2}\end{pmatrix}\begin{pmatrix}
y^{\prime}_{1}\\
y^{\prime}_{2}
\end{pmatrix}}\end{align*}

基底$\begin{pmatrix}
\boldsymbol{e}_{1} &\boldsymbol{e}_{2}\end{pmatrix}$で考えると以下の関係を得ることができます。

\begin{align*}
\boldsymbol{x}^{\prime}&=P\boldsymbol{y}^{\prime}
\tag{11}
\end{align*}

少々ややこしいですが、$\begin{pmatrix}
y^{\prime}_{1}\\
y^{\prime}_{2}
\end{pmatrix}$と成分だけを書いても基底に取り方で表しているベクトルが違うんですよね。
基底を$\begin{pmatrix}
\boldsymbol{e}^{\prime}_{1}&\boldsymbol{e}^{\prime}_{2}
\end{pmatrix}$でとった場合は$\begin{pmatrix}
\boldsymbol{e}^{\prime}_{1}&\boldsymbol{e}^{\prime}_{2}
\end{pmatrix}\begin{pmatrix}
y^{\prime}_{1}\\
y^{\prime}_{2}
\end{pmatrix}$は$\boldsymbol{x}^{\prime}$ですが、基底を$\begin{pmatrix}
\boldsymbol{e}_{1}&\boldsymbol{e}_{2}
\end{pmatrix}$でとった場合は$\begin{pmatrix}
\boldsymbol{e}_{1}&\boldsymbol{e}_{2}
\end{pmatrix}\begin{pmatrix}
y^{\prime}_{1}\\
y^{\prime}_{2}
\end{pmatrix}$は$\boldsymbol{y}^{\prime}$を表しています。

何度も言いますが、成分が変わっていなくて基底を変えたということは当然$\boldsymbol{x}^{\prime}$と$\boldsymbol{y}^{\prime}$は違うベクトルになっています。
そのことは、基底を$\begin{pmatrix}\boldsymbol{e}_{1}&\boldsymbol{e}_{2}
\end{pmatrix}$にそろえた(11)を見るとよくわかります。$\boldsymbol{x}^{\prime}$と$\boldsymbol{y}^{\prime}$は$P$を介して関係づけられています。

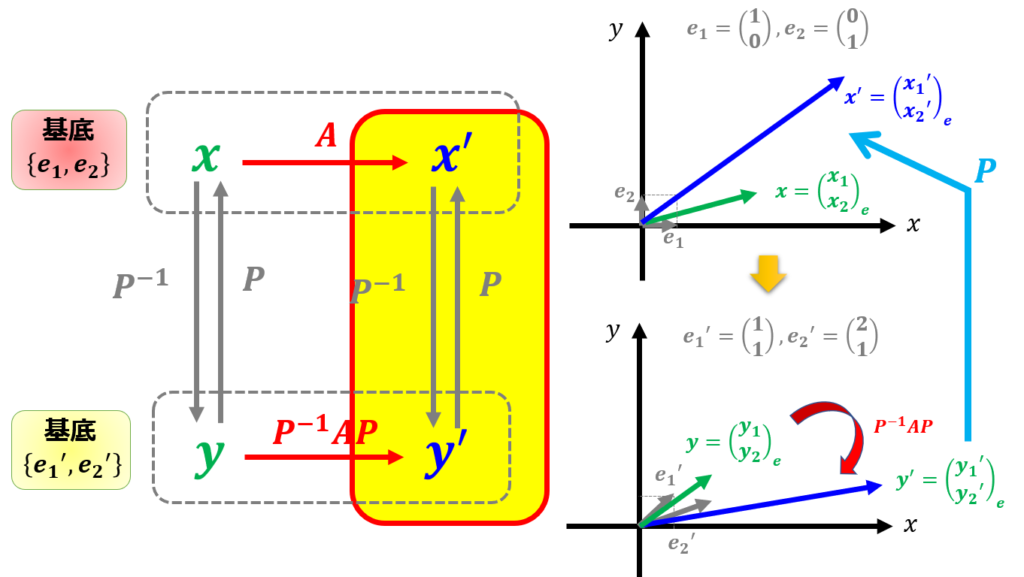
このようになります(^^)/

何度も繰り返しになりますが、本記事ではどの基底を使ったときの表現なのかをわかるように書いてきました。
以下のルールを適用することで迷子にならずに進めることができました。

$\boldsymbol{x}=\begin{pmatrix}
x_{1}\\
x_{2}\\
\end{pmatrix}_{e}$：右下に添え字で基底を表記
$\boldsymbol{x}=\underset{基底がわかる\\ように列ベクトル\\で書く}{\begin{pmatrix}
\boldsymbol{e}_{1}&
\boldsymbol{e}_{2}
\end{pmatrix}}\begin{pmatrix}
x_{1}\\
x_{2}\\
\end{pmatrix}$

このようにルールを決めて進める意義をわかっていただけれたと思います。

$n$次元に拡張できる

絵で視覚的に理解てきた方が良いので、あえて2次元で解説を行いましたが、$n$次元ベクトルへの拡張も容易です。

基底が$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2},\cdots,\boldsymbol{e}_{n}\}$での$n$次正方行列の線形変換$A$は、基底を変換する$n$次正方行列の変換行列$P$を用いると、新たな基底$\{\boldsymbol{e}^{\prime}_{1},\boldsymbol{e}^{\prime}_{2},\cdots,\boldsymbol{e}^{\prime}_{n}\}$では対応する$n$次正方行列の線形変換は$P^{-1}AP$となります。

基底は変換行列$P$で以下のように変換されます。

$\begin{pmatrix}
\boldsymbol{e}_{1}&\boldsymbol{e}_{2}&\cdots &\boldsymbol{e}_{n}
\end{pmatrix}=P^{-1}\begin{pmatrix}
\boldsymbol{e}^{\prime}_{1}&\boldsymbol{e}^{\prime}_{2}&\cdots &\boldsymbol{e}^{\prime}_{n}
\end{pmatrix}$
もしくは、
$\begin{pmatrix}
\boldsymbol{e}^{\prime}_{1}&\boldsymbol{e}^{\prime}_{2}&\cdots &\boldsymbol{e}^{\prime}_{n}
\end{pmatrix}
=P\begin{pmatrix}
\boldsymbol{e}_{1}&\boldsymbol{e}_{2}&\cdots &\boldsymbol{e}_{n}
\end{pmatrix}$

新たな基底$\{\boldsymbol{e}^{\prime}_{1},\boldsymbol{e}^{\prime}_{2},\cdots,\boldsymbol{e}^{\prime}_{n}\}$での成分の線形変換は、

\begin{align*}
\boldsymbol{y}^{\prime}=P^{-1}AP\boldsymbol{y}
\tag{7}
\end{align*}

となります。
元の基底$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2},\cdots,\boldsymbol{e}_{n}\}$での成分に戻したい場合は

\begin{align*}
\boldsymbol{x}^{\prime}=P\boldsymbol{y}^{\prime}
\tag{11}
\end{align*}

とれば元に戻ります。

まとめ

本記事のまとめです。

基底は変換行列$P$で以下のように変換されます。

①$\boldsymbol{x}$を基底$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$から別の基底$\{\boldsymbol{e}_{1}^{\prime},\boldsymbol{e}_{2}^{\prime}\}$での成分に変換します。

\begin{align*}
\boldsymbol{y}=P^{-1}\boldsymbol{x}
\end{align*}

②新たな基底$\{\boldsymbol{e}^{\prime}_{1},\boldsymbol{e}^{\prime}_{2}\}$での成分の線形変換は、

\begin{align*}
\boldsymbol{y}^{\prime}=P^{-1}AP\boldsymbol{y}
\tag{7}
\end{align*}

となります。
③元の基底$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$の成分に戻したい場合は

\begin{align*}
\boldsymbol{x}^{\prime}=P\boldsymbol{y}^{\prime}
\tag{11}
\end{align*}

とれば元に戻ります。

元の基底$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$のまま線形変換$\boldsymbol{x}^{\prime}=A\boldsymbol{x}$の計算は、1回別の基底$\{\boldsymbol{e}^{\prime}_{1},\boldsymbol{e}^{\prime}_{2}\}$での成分で線形変換$\boldsymbol{y}^{\prime}=P^{-1}AP\boldsymbol{y}$を行い、元の基底の成分に戻して$\boldsymbol{x}^{\prime}=P\boldsymbol{y}^{\prime}$としても結果は同じということです。

どうしてわざわざ別の基底に移して元の基底に対応する線形変換を用いる必要があるのかと疑問に思うかもしれませんが、次回に詳しく解説を行います。

簡単に理由を説明すると、もし別の基底を上手いこと選ぶことができて、その基底での対応する線形変換が$P^{-1}AP=\begin{pmatrix}
\alpha_{1} &0\\
0&\alpha_{2} \end{pmatrix}$のように対角行列にすることができたら計算がものすごく楽になりますよね。

計算のイメージを簡単に話すと、行列$A=
\begin{pmatrix}
4 & -2 \\
1 & 1 \\
\end{pmatrix}$という線形変換行列は全ての行と列に数字が入っているので$A\boldsymbol{x}$を計算しようものなら結果が$A\boldsymbol{x}=
\begin{pmatrix}
4 & -2 \\
1 & 1 \\
\end{pmatrix}\begin{pmatrix}
x_1 \\
x_2 \\
\end{pmatrix}=\begin{pmatrix}
4x_1-2x_2 \\
x_1+x_2 \\
\end{pmatrix}$の行列の掛け算を行うよりも、もし行列$A$が対角行列で$A^{\prime}=\begin{pmatrix}
\alpha_{1} & 0\\
0 & \alpha_{2} \\
\end{pmatrix}$のような対角成分にのみ値を持つ行列になってくれていたら、なんて嬉しいことでしょう。
$A^{\prime}\boldsymbol{y}=\begin{pmatrix}
\alpha_{1} & 0\\
0 & \alpha_{2} \\
\end{pmatrix}\begin{pmatrix}
y_{1}\\
y_{2}
\end{pmatrix}=\begin{pmatrix}
\alpha_{1}y_{1}\\
\alpha_{2}y_{2}
\end{pmatrix}$のように簡単に計算できますよね。

このような都合の良く行列$A$が対角行列$A^{\prime}$になってくれればいいのですが・・・

実は下記の記事で解説したような固有値方程式$A\boldsymbol{x}=\alpha\boldsymbol{x}$から得られる固有ベクトルを新たな基底として採用することで、その基底での線形変換は固有値を対角成分に持つ線形変換$P^{-1}AP=\begin{pmatrix}
\alpha_{1} &0\\
0&\alpha_{2} \end{pmatrix}$の形で表すことができます。