【例題演習】クラメルの公式を使って連立方程式を解く

前回では連立方程式を解くための公式であるクラメルの公式についての内容をまとめました。

前回の記事はこちら

今回はクラメルの公式を使って具体的な連立方程式の解を求める例題演習を行います。

本記事の内容

次の連立方程式の解$x,y,z$をクラメルの公式を使って求めます。

\begin{align*}
\left\{\begin{matrix}
z+y+z&=&1\\
ax+by+cz&=&d\\
a^2 x+b^2y +z^2 z&=&d^2
\end{matrix}\right.\tag{1}
\end{align*}

これから線形代数を学ぶ学生や社会人のために「役に立つ内容にしたい」という思いで記事を書いていこうと考えています。

こんな人が対象

行列をはじめて習う高校生・大学生
仕事で行列を使うけど忘れてしまった社会人

この記事の内容をマスターして行列計算を楽に計算できるようになりましょう(^^)

クラメルの公式のまとめ
3つの連立方程式を行列にする
ステップ1：行列式$|A|$を計算
$|A_{i}|$を求める
$x_{i}=\frac{|A_{i}|}{|A|}$
まとめ
参考にする参考書はこれ

クラメルの公式のまとめ

前回の記事で解説したクラメルの公式のまとめを載せておきます。

クラメルの公式のまとめ

未知数$x_{1},x_{2},\cdots ,x_{n}$の$n$個に対して連立方程式から解を求めることを考えます。

\begin{align*}
\left\{\begin{matrix}
a_{11}x_{1}+a_{12}x_{2}+\cdots +a_{1n}x_{n}=b_{1}\\
a_{21}x_{1}+a_{22}x_{2}+\cdots +a_{2n}x_{n}=b_{2}\\
\cdots\\
a_{n1}x_{1}+a_{n2}x_{2}+\cdots +a_{nn}x_{n}=b_{n}
\end{matrix}\right.
\end{align*}

これは$AX=B$のように行列でまとめることができ、$X$の$i$成分である$x_{i}$は以下で求まります。

\begin{align*}
x_{i}&=\frac{1}{|A|}\sum_{j=1}^{n}b_{j}\tilde{a}_{ji}\\
&=\frac{|A_{i}|}{|A|}
\end{align*}

※$|A_{i}|$は$i$列を縦行列$B$に置き換えた行列式

(1)はこのまとめを見ながら計算を行います。

求めるのは、$x_{i}=\frac{|A_{i}|}{|A|}$の

行列式$|A|$
$i$列を$B$に置き換えた行列式$A_{i}$

の２つですね。

3つの連立方程式を行列にする

こちらの連立方程式を行列にするところから始めましょう。

\begin{align*}
\left\{\begin{matrix}
z+y+z&=&1\\
ax+by+cz&=&d\\
a^2 x+b^2y +z^2 z&=&d^2
\end{matrix}\right.\tag{1}
\end{align*}

(1)は以下のような行列に書き換えることができます。

\begin{align*}
\underset{A}{\begin{pmatrix}
1 &1 &1 \\
a &b &c \\
a^2& b^2 & c^2
\end{pmatrix}}
\underset{X}{\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}}=
\underset{B}{\begin{pmatrix}
1\\
d\\
d^2
\end{pmatrix}}\tag{2}
\end{align*}

$AX=B$から逆行列$|A|\neq 0$であれば、$X=A^{-1}B$より$X=\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}$が求まりますね。クラメルの公式を使うにしても$A$の逆行列$A^{-1}$を求めなくてはいけないということです。

ステップ1：行列式$|A|$を計算

まずは、行列式$|A|$を計算します。
3行3列の行列式の計算はサラスの公式を使えば簡単に求まります。

カマキリ

サラスの公式を忘れた方のために絵を載せておきます！

\begin{align*}
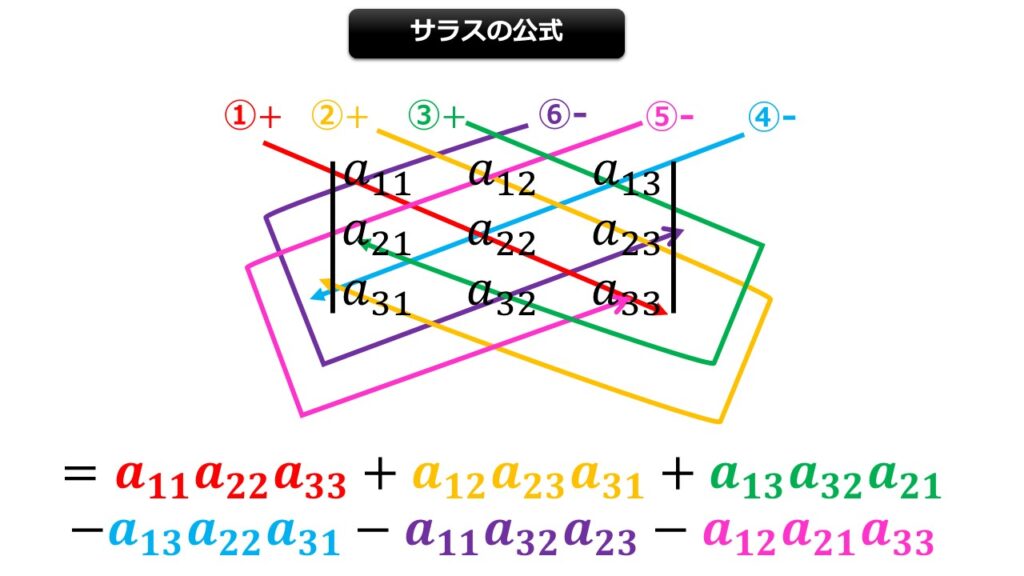
|A|&=\begin{vmatrix}
1 &1 &1 \\
a &b &c \\
a^2& b^2 & c^2
\end{vmatrix}\\
&=1\times b\times c^2+1\times c\times a^2+1\times b^2\times a\\
&= -1\times b\times a^2-1\times a\times c^2-1\times b^2\times c\\
&=(a-b)(b-c)(c-a)\tag{3}
\end{align*}

計算は少し面倒ですが(3)のようにきれいに因数分解ができます。

$|A_{i}|$を求める

次に$i$列を$b$に置き換えた行列式を計算します。

具体的には、

1列目を$B$に置き換えた$x=\begin{vmatrix}
1 &1 &1 \\
d &b &c \\
d^2& b^2 & c^2
\end{vmatrix}$
2列目を$B$に置き換えた$y=\begin{vmatrix}
1 &1 &1 \\
a &d &c \\
a^2& d^2 & c^2
\end{vmatrix}$
3列目を$B$に置き換えた$z=\begin{vmatrix}
1 &1 &1 \\
a &b &d \\
a^2& b^2 & d^2
\end{vmatrix}$

これらを計算することになります。

これもサラスの公式を使えば簡単ですね。
しかも(3)で既に似たような形の行列式を得ているため文字を置き換えるだけで結果が得られますね(^^)

1列目を$B$に置き換えた$x=\begin{vmatrix}
1 &1 &1 \\
d &b &c \\
d^2& b^2 & c^2
\end{vmatrix}=(d-b)(b-c)(c-d)$
2列目を$B$に置き換えた$y=\begin{vmatrix}
1 &1 &1 \\
a &d &c \\
a^2& d^2 & c^2
\end{vmatrix}=(a-d)(d-c)(c-a)$
3列目を$B$に置き換えた$z=\begin{vmatrix}
1 &1 &1 \\
a &b &d \\
a^2& b^2 & d^2
\end{vmatrix}=(a-b)(b-d)(c-d)$

以上で計算が終了です(^^)

$x_{i}=\frac{|A_{i}|}{|A|}$

$x_{i}=\frac{|A_{i}|}{|A|}$を具体的に書いて問題の解答は終わりです。

\begin{align*}
\left\{\begin{matrix}
x=\frac{(d-b)(b-c)(c-d)}{(a-b)(b-c)(c-a)}\\
y=\frac{(a-d)(d-c)(c-a)}{(a-b)(b-c)(c-a)}\\
z=\frac{(a-b)(b-d)(d-a)}{(a-b)(b-c)(c-a)}
\end{matrix}\right.\tag{1}
\end{align*}

連立方程式が解くことができました。