こんにちは(@t_kun_kamakiri)(^^)/
線形代数は、理系なら大学の初学年で必ず学ぶ学問ですね。
当ブログでは線形代数の内容についてのいちから解説する記事を書いていこうと考えています。
- 線形代数の実用面での重要性
- 線形代数が使われる場面
- 記事を書くにあたっての方針
これから線形代数を学ぶ学生や社会人のために「役に立つ内容にしたい」という思いで記事を書いていこうと考えています。
ところで、線形代数ってなんでしょうか?
線形代数は、線形空間と線形変換を考える数学の一分野です。
とりあえず、線形代数はベクトルや行列を取り扱う学問だと考えても良いでしょう。
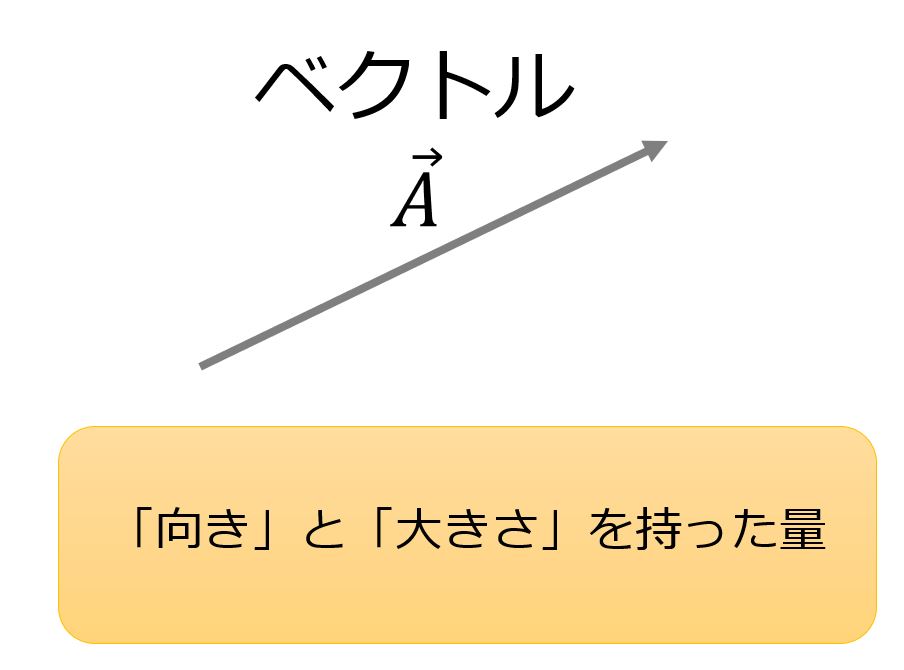
ベクトルは高校生でも習うように、大きさと向きを持つ量ですね。
しかし、行列は高校生では習わないかもしれないです。


余談ですが、僕は大学に入る前に浪人をしたので、浪人中の予備校で数Cで行列の勉強をしました。
2007年度では大学入試の科目に数C(行列も含む)があったんですよね。
なので、大学に入ってから線形代数で行列が出てくるのですが、そこまで新しいことを学ぶ感じはしませんでした。
ですが、行列というのは高校生のカリキュラムで習ったり習わなかったり微妙なところです。
もし、行列を習ったことがない学生が大学の線形代数を見ると、慣れるのにかなり時間がかかると思います。
大学生に入りたての授業での「線形代数」をはじめ、「微積」「力学」でも行列計算が出てくるため、線形代数で挫折すると今後が悲惨です。
「力学」の問題なんて高校生で習った以上に何を大学で学ぶのかと思うかもしれませんが、いきなり基底ベクトル(?)を用いて運動方程式を書き、それを微分方程式の知識で解くというのをいきなりやります・・・
はじめは、「基底ベクトルってなんですか?」という状態で、線形代数を勉強するうちにやっと理解をしていきます。
しかし、大学に入学して線形代数を勉強して三か月くらいたってようやく力学の授業が理解できてくるという状況です。
僕自身、大学入学の最初の三か月は「線形独立な元を使って線形結合で書く」など色々わかっていない状況で授業が進んでいったのを今でも覚えています。
このように、線形代数は大学ではじめて学ぶ数学でありながら、挫折するとあとはついていけないっていう最初の難関科目と言っても良いでしょう・・・・
線形代数は実用面でもかなり使う
線形代数は、理系の道でやっていこうと思うのであれば必ず身に付けて、自由に使いこなせるようになっていないといけません。
なぜなら線形代数は実用面でも多くの場面で使いますから。
先ほど線形代数はベクトルや行列を扱う数学の一分野と考えてよいというお話をしました。
ここでは、ベクトルや行列を扱う物理の学問について以下列挙してみます。
- 力学
- 電磁気学
- 流体力学
- 量子力学
- 相対性理論
- 材料力学(塑性力学)
多分もっと多くの学問で必要とされているはずですが、思いついたのを列挙しておきました。ベクトルや行列を使わない物理の学問ってあるのかというくらいよく使います。
特に、変数が多くなったときにまとめるために行列計算を使って計算を進めたりします。
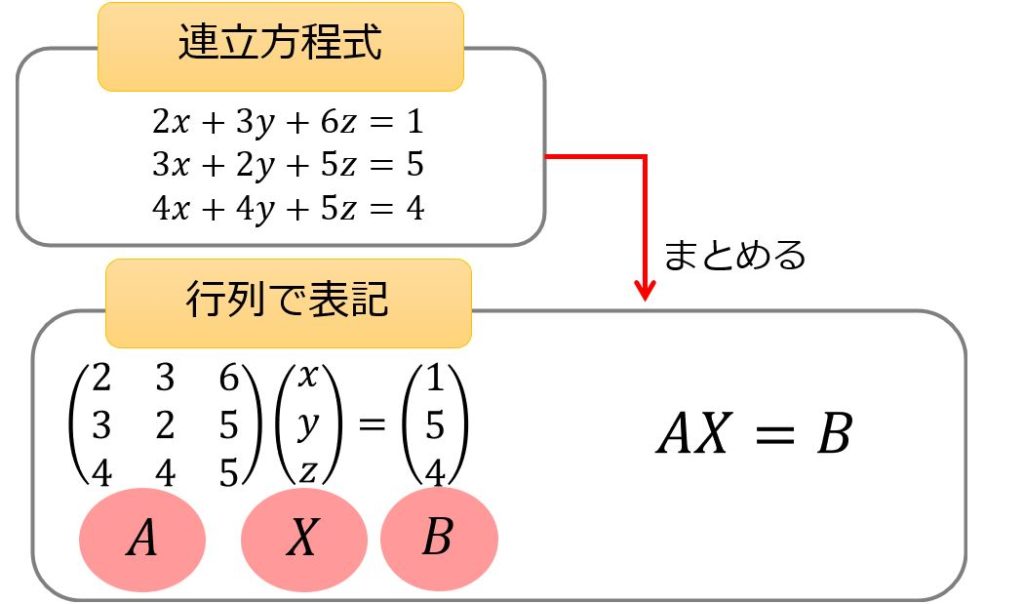

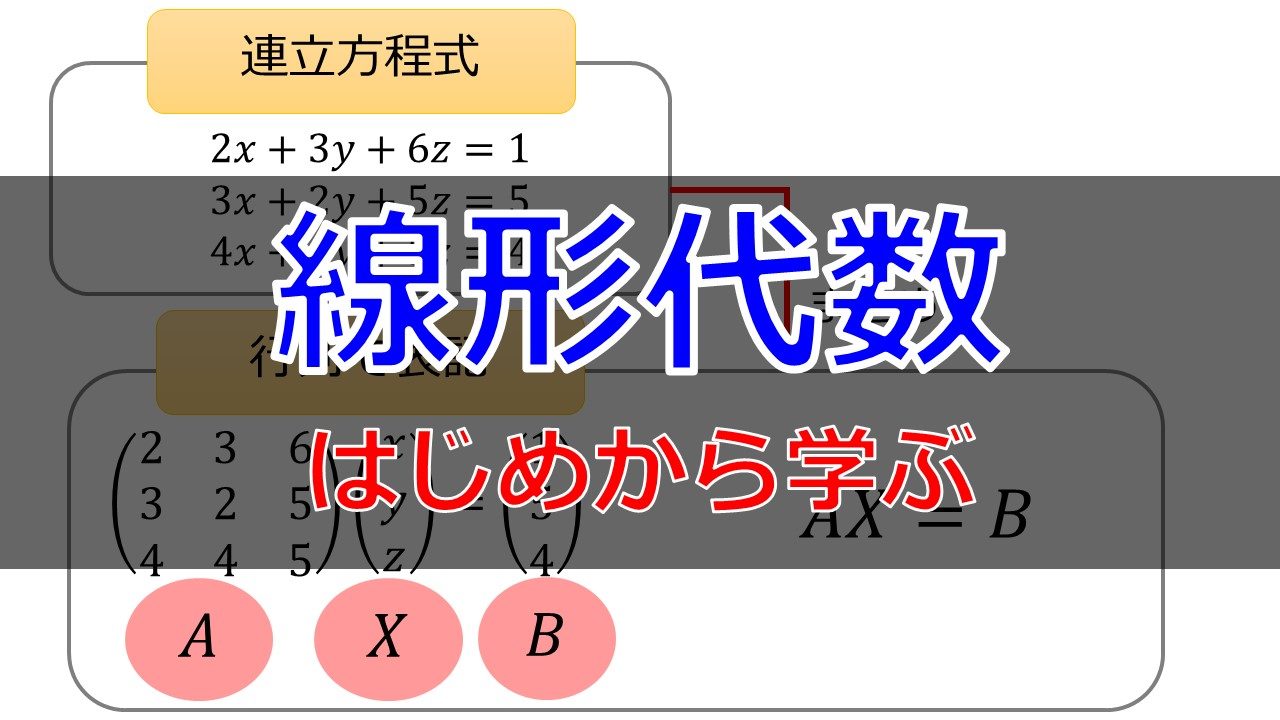
連立方程式を行列の形で書くととてもすっきりしますよね。
実用面では、数値計算で有名な有限要素法などの連立方程式の解法でも使われます。
数値計算のしやすさからも行列計算は多用されます。
行列計算を自由に行うためには、これから学ぶ線形代数の計算の特有の技術について学んでおく必要があります。
線形代数は必ず身に付けておかなければ、その先の専門科目では手も足も出ない場面に出くわしてしまいますので、大学初学年の早いうちにマスターしておくことが必須です。
社会人になっても使う線形代数
大学のはじめの線形代数で挫折することなく頑張って勉強をしたため、線形代数の基礎は大学でも初学年で身に付けることができたのでその後の授業はスムーズについていくことができたと思います。
社会人になった現在でも線形代数はよく出てきます。
繰り返しになりますが、行列計算を取り扱う場面が多いため、必然的に線形代数の知識は必要になってきます。
特に、複雑な連立方程式を解く場合が多いので、行列計算は連立方程式をきれいに整理するのにとても役に立ちます。
連立方程式を解法の際にも線形代数での計算の技術はよく使います。
線形代数の記事を書いていこう(^^)/
そんな理由もあって、大学の理系初学者には挫折することなく大学の理系ライフを送ってほしいということで、線形代数の計算方法でつまづいたら、
「ここにちゃんと解説があるよ」
という立ち位置で本記事の「線形代数シリーズ」を書いていこうと思います。
僕自身もいちから復習をしながら書いていくため、たぶん書いている本人が一番勉強になるはずです。
参考にする参考書はこれ
一から順序立てて説明しようとすると膨大な時間がかかります。
当ブログでは、以下の2つの参考書を読みながらよく使う内容をかいつまんで、一通り勉強すればついていけるような内容を目指していこうと思います。
大事なところをかいつまんで、「これはよく使うよな。これを理解するためには補足で説明をする」という調子で進めていきます(^^)/
「線形代数」の記事内容の方針
線形代数を一通り学んでも、それを実用面で使えないといけません。
例えば、連立の方程式の解法のときに、線形代数で習った計算方法を駆使すれば、驚くほど簡単に答えを出すことができます。
特に、有用なのはPCのパワーを使って数値計算を行うときだろうと考えています。
プログラムの中には、線形代数の数値計算ライブラリが用意されているものもあります(Pythonなど)。
記事の内容は、「基本の理解」と「実用面で使う場面」の2つを意識して書いていこうと考えています。
本シリーズを見ることで、線形代数のありがたさがわかってもらえれば幸いです(^^)