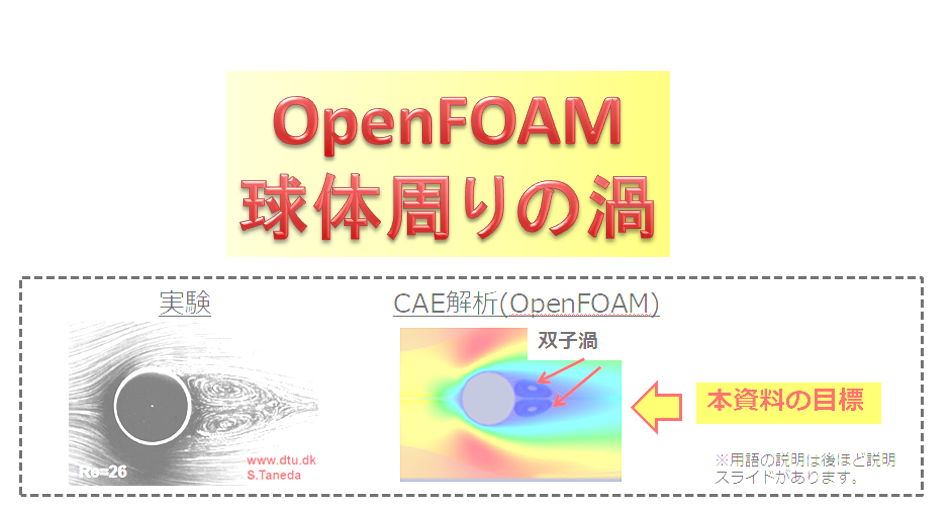
この記事は3つのキーワードをもとに解説していくことになります。
キーワード
- 逆関数
- 指数関数
- 対数関数
本記事の内容では、
指数関数\(y=e^{x}\)の逆関数が\(y=log_{e}x\)であることの解説をします。
まずは、逆関数とは何かってところから順に話を進めていきましょう。
グラフの作成には、Pythonを使います。
逆関数とは?
逆関数とは何でしたかというと、
「\(y\)を\(x\)の関数\(y=f(x)\)とし、それを\(x\)について解き\(x=g(y)\)となったとします。
これを\(x\)と\(y\)を入れ替えて\(y=g(x)\)としたときの\(g\)を逆関数という。」
全然よくわからない文言になってしまいました(笑)
逆関数を作るには\(x\)と\(y\)を入れ替えれば良い
具体例を見て、理解をした方が良いでしょう。
というグラフを書くことにします。
範囲:\(0\leq x\)
※範囲を指定しているのには意味があります(後ほど解説)
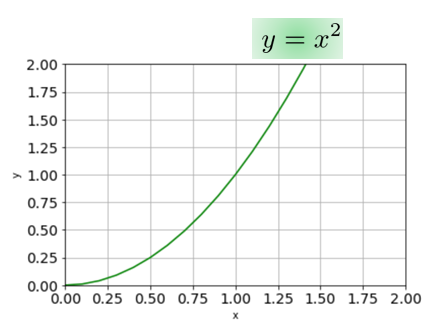
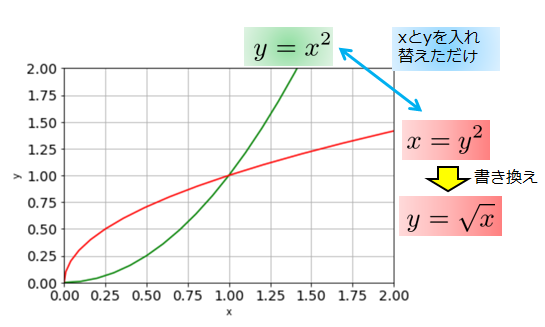
逆関数作るには、この\(y=x^{2}\)の\(x\)と\(y\)を入れ替えれば良いということなのです。
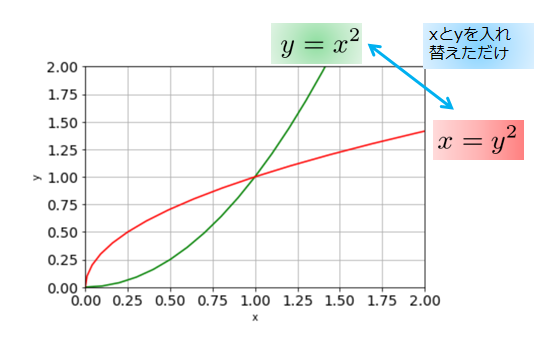
\(y=x^{2}\)の逆関数は、赤ライン\(x=y^{2}\)ということになります。
しかし、関数を書くときには「\(y=\)」という形にしているのが慣習なので、\(x=y^{2}\)を\(y=\sqrt{x}\)と書くようにします。
なので、
逆関数を作るときに、\(x\)と\(y\)を入れ替える操作をしたわけですから、当然「元の関数と、その逆関数の関係は\(y=x\)に対して鏡のような関係(対称)」となります。
実際、グラフに書いてみましょう。
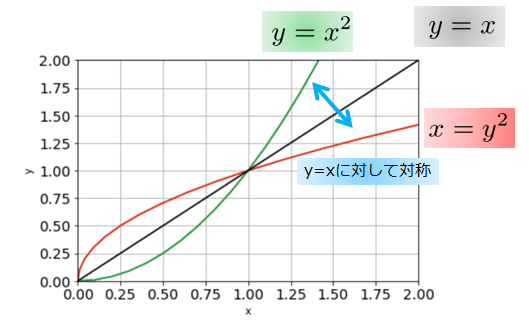
\(y=x\)に対して対称な関係にあることがわかりますね。
Pythonコード
上のグラフを書くためのPythonコードを記載しておきます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | import numpy as np import matplotlib.pyplot as plt x=np.arange(0,5,0.1) y=x y1=x**2 #y1=np.log(x) #y2=np.exp(x) plt.plot(x,y1,color="green") plt.plot(y1,x,color="red") plt.plot(x,y,color="black") #x軸、y軸の範囲 plt.xlim([0,2]) plt.ylim([0,2]) #フォントサイズ plt.xticks(fontsize=14) plt.yticks(fontsize=14) #ラベル plt.xlabel("x") plt.ylabel("y") #グリッド生成 plt.grid() plt.show() |
逆関数を作るためにしたことは、元の関数に対してグラフを書くときに\(x\)と\(y\)の軸を入れ替えただけです。
逆関数を作る際の注意点:xの範囲に注意
逆関数を作るときや、高校数学の問題で逆関数を扱う場合に注意すべき点があります。
それは逆”関数”であるということです。
中学生の数学で関数を習ったときに、「関数とは、\(x\)をひとつ決めればただひとつの\(y\)が決定する」というような言い方で習うのです。(少なくとも高校までの範囲では・・・大学の数学は知りません)
だから、\(x\)と\(y\)の軸を入れ替えた操作後も関数の性質をちゃんと持っている必要があります。
\(x\)と\(y\)の軸を入れ替えた操作後に、「ひとつの\(x\)に対して、複数の\(y\)が求まる」ような状態では逆関数とは言わないのです。
例えば関数ではない例として、円の方程式
$$x^2+y^2=r^2$$
などは「円の関数」という言い方をしないわけです。
なぜなら「ひとつの\(x\)に対して\(y\)がふたつ決まってしまう」からです。
先ほどの例でも、もし範囲を\(0\leq x\)ではなく、どんな\(x\)でもOKですよということにして、
の逆関数を描くと・・・・・下記のような感じになります。
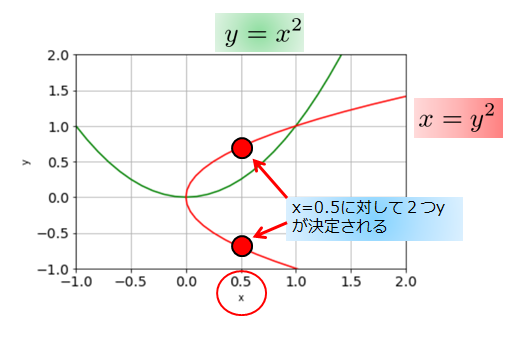

例えば、\(x=0.5\)に対して2つの\(y\)が決定されることになるので、これは関数とは言いません。
(大学の数学ではどう扱うかは知りませんが・・・)
これの何が困るかってことですが・・・・・・ひとつ思い浮かぶのは、積分できないではないか!ってことです。
どっちの\(y\)の値を使って積分(足し合わせていく)すれば良いのかということになります。
だから、逆関数を作る前に\(x\)の範囲は必ずどこかに限定するなど注意をする必要があります。
※単調増加や単調減少の場合は\(x\)の範囲の指定は気にしなくても良いです。
指数関数の逆関数は対数関数
では、いよいよ指数関数の逆関数を作ってみたいと思います。
指数関数
わかりやすい指数関数の代表例として、
と、ネイピア数\(e\)を使いましょう。
※逆関数を作る注意点として、\(x\)の範囲を注意しなくてはいけませんが、\(y=e^{x}\)は単調増加の関数あるため、\(x\)と\(y\)を入れ替えたとしてもやはり単調増加なので、\(x\)の範囲は気にしなくても良いことになります。
では、グラフを書いてみましょう。
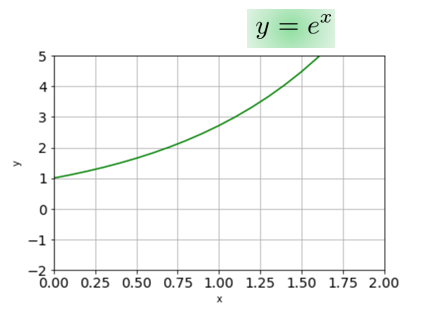

単調増加ですね。
では、次に\(y=e^{x}\)の逆関数を作ってみましょう・・・・・・
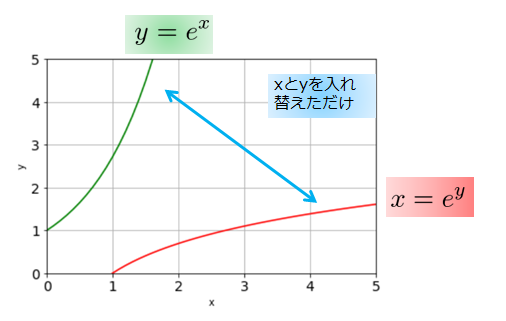

↑このように逆関数をつくる手続き上は、\(x\)と\(y\)を入れ替えるだけで良いのです。
何も難しいことがありません。
しかし、\(x=e^{y}\)の形にはしたのは良いが・・・・
「はて、どうやって\(x=e^{y}\)から「\(y=\)」の形を作るんだ」ってなるでしょう(笑)
\(x=e^{y}\)の場合は\(y=x^{2}\)のように簡単には「\(x=\)」の形にいけそうにないのです。肩に乗っている\(x\)を何とか下におろしたくなる衝動にかられます。
ここで、「なるほど・・・・・だから高校数学で対数\(log\)を習うのか」と、ようやく気付きます。
対数関数
では、(2)式の両辺に\(\log_{e}\)を作用させることにします。
そうすると、
となるので、「\(y=\)」という形にできました。
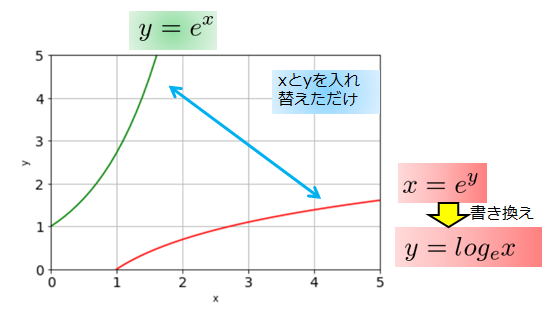
では、指数関数\(y=e^{x}\)と対数関数\(y=\log_{e}x\)も\(y=x\)に対して対称なのかを見てみましょう。
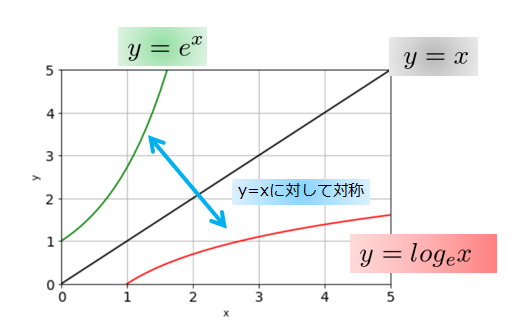


\(y=x\)に対して対称な関係にあることがわかりますね。
逆関数は、\(x\)と\(y\)を入れ替える操作をしたわけですから、
当然「指数関数の逆関数である対数関数は関係\(y=x\)に対して鏡のような関係(対称)」となります。
Pythonコード
上記のグラフを書くのに使用したPythonコードを載せておきます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 | import numpy as np import matplotlib.pyplot as plt x=np.arange(0.0001,10,0.1) y=x y1=np.exp(x) y2=np.log(x) plt.plot(x,y1,color="green") plt.plot(x,y2,color="red") plt.plot(x,y,color="black") #x軸、y軸の範囲 plt.xlim([0,5]) plt.ylim([0,5]) #フォントサイズ plt.xticks(fontsize=14) plt.yticks(fontsize=14) #ラベル plt.xlabel("x") plt.ylabel("y") #グリッド生成 plt.grid() #凡例 #plt.legend() plt.show() |
指数関数と対数関数を作るのに、
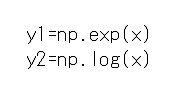
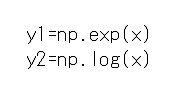
と定義しています。
※もちろん\(y=x^2\)の例で示したように、グラフで対数関数を書くだけなら指数関数の\(x\)と\(y\)を入れ替えれば良いのですから、
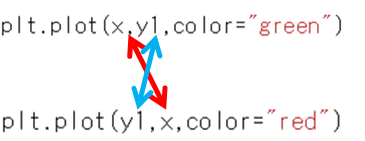
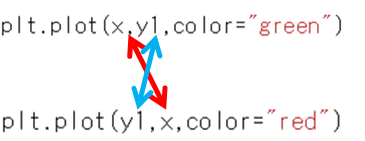
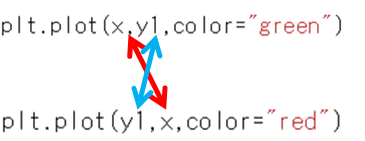
と書いても指数関数と対数関数の関係は図示できます。
まとめ
逆関数を作るときは、\(x\)の範囲に注意すること。
元の関数と、その逆関数の関係は\(y=x\)に対して鏡のような関係(対称)である。
指数関数の逆関数は対数関数である。
指数関数\(y=e^{x}\)の逆関数は、赤ライン対数関数\(y=log_{e}x\)となります。