こんにちは(@t_kun_kamakiri)
本記事ではC++を使った1次元拡散方程式を題材にオブジェクト指向でのコーディングを解説します。
コードの解説は以下の記事に詳しく書いています。
1次元の拡散方程式をC++で数値計算
C++は3か月前に勉強を始めたばかりなのでコーディングスタイルの良し悪しに関してはこれからもっと磨いていかないといけないと思っています。今回はアウトプットの場として勉強したことをメモとして残しておきます。
【環境】
Microsoft Visual C++ (Visual Stido 2022)
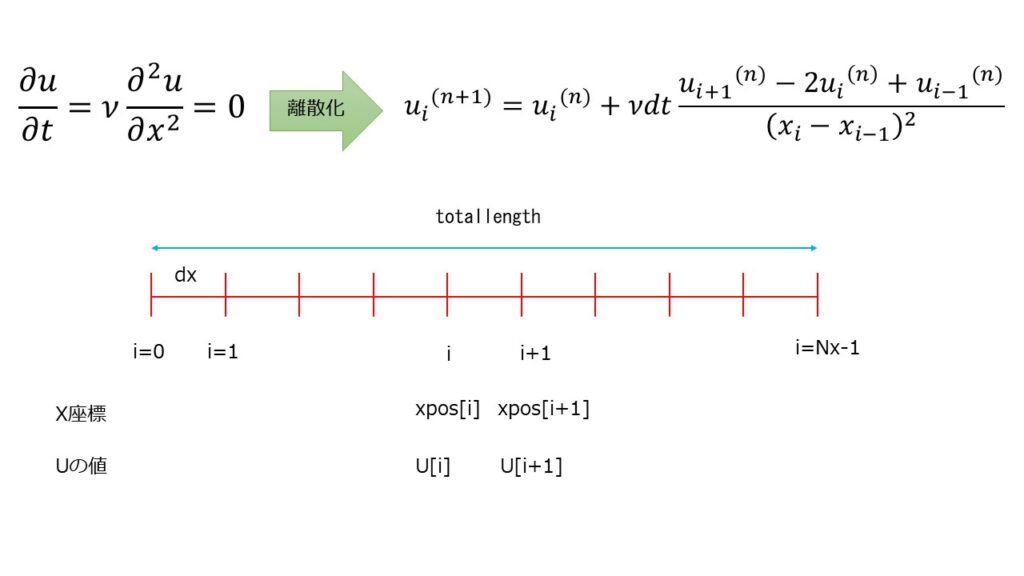
解く方程式
コードは前回の記事のを利用します。
コードの解説は以下の記事に詳しく書いています。
コードの修正
まずは2階微分の中心差分による離散化$\frac{\partial^2 u}{\partial x^2}=\frac{u_{i+1}-2u_{i}+u_{i-1}}{dx^2}$をDiff1d.hに定義します。
1 2 3 4 | Fields::vectorField1d laplacianX1d(Fields::vectorField1d& vec) { (省略) } |
Diff1d.h
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 | #include "Fields.h" #include <vector> #include <cmath> //add using std::vector; namespace fd1d { // U U U U //*-----*----*----* // i-1 i Fields::vectorField1d gradX1d(Fields::vectorField1d& vec) { Fields::vectorField1d temp = vec; for (int i = 1; i < vec.size() - 1; i++) { temp[i].value = (vec[i].value - vec[i - 1].value) / (vec[i].x1d - vec[i - 1].x1d); } return temp; } // add Fields::vectorField1d laplacianX1d(Fields::vectorField1d& vec) { Fields::vectorField1d temp = vec; for (int i = 1; i < vec.size() - 1; i++) { temp[i].value = (vec[i + 1].value - 2.0 * vec[i].value + vec[i - 1].value) / pow((vec[i].x1d - vec[i - 1].x1d), 2.0); } return temp; } } |
$dx^2$を計算するために冒頭で「#include <cmath>」をインクルードし、「pow((vec[i].x1d – vec[i – 1].x1d), 2.0);」で2乗を計算しています。
Solution1d.hのSolution1d関数の引数3つにします。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | #ifndef SOLUTION_H #define SOLUTION_H class Solution1d { public: Solution1d(int&, double&, double&); // constructor virtual ~Solution1d(); //deconstructor int nt; //ステップ数 double dt; //時間刻み幅 double visc; //粘性係数 }; #endif |
同様にSolution1D.cppのSolution1d関数の引数も3つにします。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | #include <iostream> #include "Solution1D.h" Solution1d::Solution1d(int& nt_, double& dt_, double& visc_) : nt(nt_), dt(dt_), visc(visc_) { std::cout << "Solution1d()" << std::endl; } Solution1d::~Solution1d() { } |
次にmain.cppの、
1 2 | Fields::vectorField1d Diff = fd1d::gradX1d(U); Unew = U - (cdt * Diff); // du/dt = c*du/dx => unew{i} = u{i} - c*dt(u{i} - u{i-1})/dx |
を以下に変更します。
1 2 | Fields::vectorField1d Diff2 = fd1d::laplacianX1d(U); Unew = U + sol1d.dt * sol1d.visc * Diff2; |
先ほどSolution1d.hとSolution1d.cppでSolution1d関数の引数を3つにしたので、main.cppでも以下のように粘性係数viscを定義し、「Solution1d sol1d(ntimestep, dt, visc);」でインスタンス化するときの引数を3つにします。
1 2 3 | double visc = 1e-3; Solution1d sol1d(ntimestep, dt, visc); |
拡散方程式による初期状態からの拡散を見るためにタイムステップ数を大きくします。
1 | int ntimestep = 10000; |
出力するファイル名を以下に変更します。
1 2 3 | string name = "1ddiffusion_initial"; string name2 = "1ddiffusion_final"; |
修正は以上です。
全体のコード
前回の記事から変更したのはmain.cppとDiff1d.hだけです。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 | #include <iostream> #include <vector> #include "Mesh.h" //メッシュ設定 #include "Fields.h" //場の定義 #include "Diff1d.h" //空間微分 #include "Solution1D.h" //時間ループ #include "FileWriter.h" //ファイル出力 #include "PrintVector.h" //場のprint文 using namespace std; using std::vector; int main() { int Nx =100; double totallength = 2.0; Mesh mesh_(Nx, totallength);//Meshクラスのインスタンス化 //Fieldsの設定 #include "creatFields.h"; //initial condition cout << "Initial :: Iteration completed, writing the final file" << endl; for (int i = 0; i < U.size(); i++) { U[i].value = 1.0; if ((U[i].x1d > 0.5) && (U[i].x1d < 1.0)) { U[i].value = 2.0; } } Unew = U; string U_name = "Unew"; PrintVector(Unew, U_name); //file writer string name = "1dBurgers _initial"; FileWriter filewriterObject_; filewriterObject_.write1dField(Unew, name); // solution int ntimestep = 1000; double dt = 0.001; double visc = 1e-3; Solution1d sol1d(ntimestep, dt, visc); for (int nt = 0; nt < sol1d.nt; nt++) { cout << "Iteration no : " << nt << endl; U= Unew; double wavespeed = 1.0; double cdt = sol1d.dt * wavespeed; Fields::vectorField1d Diff1 = fd1d::gradX1d(U); Fields::vectorField1d Diff2 = fd1d::laplacianX1d(U); //Unew = U - (cdt * Diff1); // du/dt = c*du/dx => unew{i} = u{i} - c*dt(u{i} - u{i-1})/dx // ノイマン条件 Unew[0].value = Unew[1].value; Unew[U.size() - 1].value = Unew[U.size() - 2].value; } //file writer string name2 = "1dBurgers _final"; FileWriter filewriterObject_1; filewriterObject_1.write1dField(Unew, name2); return 0; } |
creatFields.hを作ってUの設定は別のヘッダーファイルで定義するようにしました。
1 2 3 4 5 6 7 | // UFields(typedef vector<Fields> vectorField1d;) Fields FieldsOperations; Fields::vectorField1d U(mesh_.NumberOfNode); Fields::vectorField1d Unew(mesh_.NumberOfNode); U = FieldsOperations.passGridinfomation(U, mesh_.xpts); Unew = FieldsOperations.passGridinfomation(Unew, mesh_.xpts); |
さらにプログラム作成途中でU[i].vauleの値を確認したい場合に出力するプログラムをヘッダーファイルに書きました。
main.cppで
1 2 | //Fieldsの設定 #include "creatFields.h"; |
によりインクルードしています。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | #include "Fields.h" #include <iostream> #include <string> void PrintVector(Fields::vectorField1d& vec, std::string& name) { std::cout << "====== " << name << ".x1d ====== " << std::endl; for (int i = 0; i < vec.size(); i++) { std::cout << name << "[" << i << "] = " << vec[i].x1d << std::endl; } std::cout << "====== " << name << ".value ====== " << std::endl; for (int i = 0 ; i < vec.size(); i++) { std::cout << name << "[" << i << "] = " << vec[i].value << std::endl; } } |
main.cppで
1 2 | string U_name = "Unew"; PrintVector(Unew, U_name); |
の2行でよりでU[i].vauleの値を確認できます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | #ifndef MESH_H #define MESH_H #include "Mesh.h" #include <vector> using std::vector; class Mesh { public: Mesh(); //constructor Mesh(int&, double&); //引数ありconstructor virtual ~Mesh();//deconstructor int NumberOfNode;//x分割数 double lengthx;//x方向長さ double dx1d;//分割幅 vector<double> xpts;//x座標 void discritized1dgrid(vector<double>&); //x[i]の作成 }; #endif //MESH_H |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | #include "Mesh.h" #include <iostream> Mesh::Mesh() { } Mesh::Mesh(int& n, double& txlengthx): NumberOfNode(n),//x分割数 lengthx(txlengthx),//x方向長さ xpts(NumberOfNode, 0.0)//vector(要素数, 値) { dx1d = lengthx / (NumberOfNode-1); discritized1dgrid(xpts); //add } void Mesh::discritized1dgrid(vector<double>& vec) { for (int i = 1; i < vec.size(); i++) //vec[0]=0なのでi=1からループする { vec[i] = vec[i - 1] + dx1d; } } Mesh::~Mesh() { } |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 | #ifndef FIELDS_H #define FIELDS_H #include "Mesh.h" #include <vector> using std::vector; class Fields { public: Fields();//constructor virtual ~Fields(); //deconstructor typedef vector<Fields> vectorField1d; double x1d; //x座標 double value; //Uの値 Fields::vectorField1d passGridinfomation(Fields::vectorField1d&, vector<double>&); //演算子のオーバーロード friend Fields::vectorField1d operator+(const Fields::vectorField1d&, const Fields::vectorField1d&); friend Fields::vectorField1d operator-(const Fields::vectorField1d&, const Fields::vectorField1d&); friend Fields::vectorField1d operator&&(const Fields::vectorField1d&, const Fields::vectorField1d&); friend Fields::vectorField1d operator*(const double&, const Fields::vectorField1d&); friend Fields::vectorField1d operator*(const Fields::vectorField1d&, const double&); }; #endif //FIELDS_H |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 | #include "Fields.h" #include <iostream> Fields::Fields(): x1d(0.0), value(2.0) { } Fields::vectorField1d Fields::passGridinfomation(Fields::vectorField1d& vec, vector<double>& xpts_) { /* typedef vector<Fields> vectorField1d; double value; double x1d; */ for (int i = 0; i < vec.size(); i++) { vec[i].x1d = xpts_[i]; } return vec; } Fields::vectorField1d operator+(const Fields::vectorField1d& vecA, const Fields::vectorField1d& vecB) { Fields::vectorField1d temp = vecA; for (int i = 0; i < vecA.size(); i++) { temp[i].value += vecB[i].value; } return temp; } Fields::vectorField1d operator-(const Fields::vectorField1d& vecA, const Fields::vectorField1d& vecB) { Fields::vectorField1d temp = vecA; for (int i = 0; i < vecA.size(); i++) { temp[i].value -= vecB[i].value; } return temp; } Fields::vectorField1d operator&&(const Fields::vectorField1d& vecA, const Fields::vectorField1d& vecB) { Fields::vectorField1d temp = vecA; for (int i = 0; i < vecA.size(); i++) { temp[i].value *= vecB[i].value; } return temp; } Fields::vectorField1d operator*(const double& dbvalue, const Fields::vectorField1d& vecB) { Fields::vectorField1d temp = vecB; for (int i = 0; i < vecB.size(); i++) { temp[i].value = dbvalue * vecB[i].value; } return temp; } Fields::vectorField1d operator*(const Fields::vectorField1d& vecB, const double& dbvalue) { Fields::vectorField1d temp = vecB; for (int i = 0; i < vecB.size(); i++) { temp[i].value = dbvalue * vecB[i].value; } return temp; } Fields::~Fields() { } |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 | #include <vector> #include "Fields.h" #include <cmath> //add using std::vector; namespace fd1d { // U U U U //*-----*----*----* // i-1 i double returndouble(double& a) { double newdouble = a * 2.0; return newdouble; } Fields::vectorField1d gradX1d(Fields::vectorField1d& vec) //typedef vector<Fields> vectorField1d; { Fields::vectorField1d temp(vec.size()); for (int i = 1; i < vec.size(); i++) { temp[i].value = (vec[i].value - vec[i - 1].value) / (vec[i].x1d - vec[i - 1].x1d); } return temp; } Fields::vectorField1d laplacianX1d(Fields::vectorField1d& vec) //typedef vector<Fields> vectorField1d; { Fields::vectorField1d temp(vec.size()); for (int i = 1; i < vec.size() - 1; i++) { temp[i].value = (vec[i + 1].value - 2.0 * vec[i].value + vec[i - 1].value) / pow((vec[i].x1d - vec[i - 1].x1d), 2.0); } return temp; } } |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | #ifndef SOLUTION_H #define SOLUTION_H class Solution1d { public: Solution1d(int&, double&, double&); // constructor virtual ~Solution1d(); //deconstructor int nt; //ステップ数 double dt; //時間刻み幅 double visc; //粘性係数 }; #endif |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | #include <iostream> #include "Solution1D.h" Solution1d::Solution1d(int& nt_, double& dt_, double& visc_) : nt(nt_), dt(dt_), visc(visc_) { std::cout << "Solution1d()" << std::endl; } Solution1d::~Solution1d() { } |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | #ifndef FILEWRITWE_H #define FILEWRITWE_H #include <stdio.h> #include <iostream> #include <vector> #include <cmath> #include <string> #include <cstring> #include <sstream> #include <fstream> //ファイルの書き込みに必要 #include "Fields.h" using namespace std; using std::vector; using std::string; class FileWriter { public: FileWriter();//constructor virtual ~FileWriter(); //destructor void write1dField(Fields::vectorField1d&, string&); }; #endif |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 | #include "FileWriter.h" #include <iostream> FileWriter::FileWriter() { } void FileWriter::write1dField(Fields::vectorField1d& vec, string& name_) { string myfileType = ".dat"; //拡張子 string path = "C:\\work\\C_lang\\20220413_diff_C_puls\\\004_NS_Eq_1D_blog\\1DNS\\1DNS\\"; //絶対パス string pathName = path.append(name_).append(myfileType); //"myOutput;" + ".dat" => "myOutput.dat" std::cout << "pathName = " << pathName << " : pathName.size() = " << pathName.size() << std::endl; FILE* outfile; fopen_s(&outfile, pathName.c_str(), "w+t"); //https://www.paveway.info/entry/2018/12/25/cpp_std_string_char std::cout << "outfile = " << &outfile << std::endl; for (int i = 0; i < vec.size(); i++) { double xpos = vec[i].x1d; double uvel = vec[i].value; if (outfile) { fprintf(outfile, "%5.8lf\t%5.8lf\n", xpos, uvel); } } fclose(outfile); } FileWriter::~FileWriter() { } |
出力結果の確認
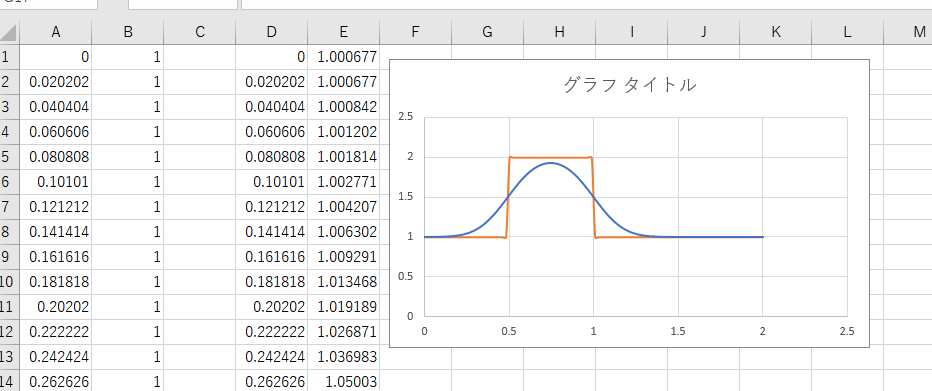
計算を実行し、計算が終了すると以下の2つのファイルができています。
- 1ddiffusion_initial.dat:初期状態
- 1ddiffusion_final.dat:最終状態
今回はさくっと確認するためExcelで重ねてみました。
- オレンジ:初期状態
- 薄青:最終状態(10000ステップ目)