こんにちは（@t_kun_kamakiri）(‘◇’)ゞ
↓こちらの記事で3種類の熱の伝わり方について解説を行いました。
今回の記事では電子機器の冷却フィンについて具体的な熱の計算を行いたいと思います。
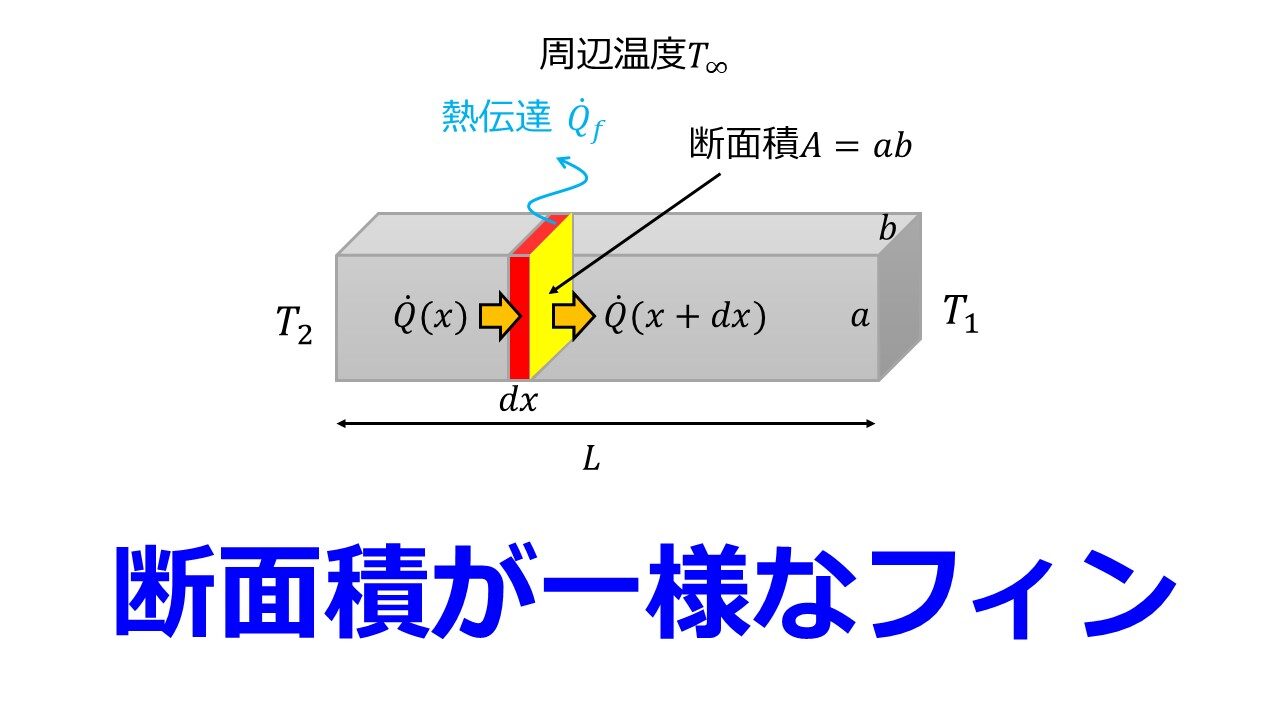
以下のようなシンプルなモデルでフィンの温度分布がどのようになるのかを計算します。
【パターン1】立方体形状
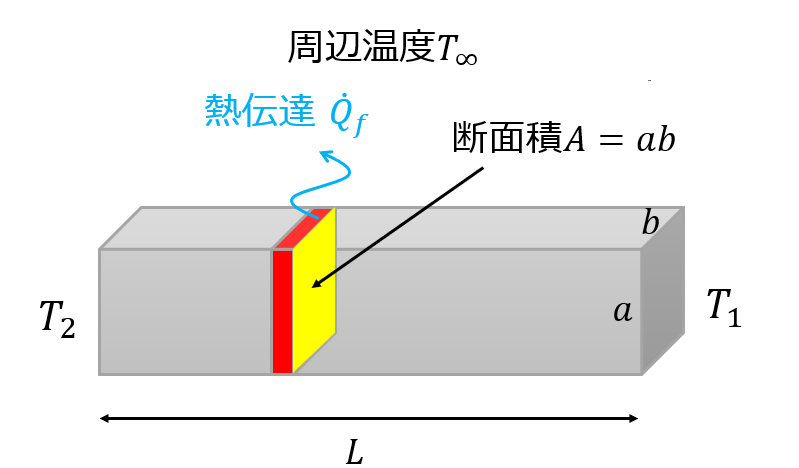
【パターン2】円筒形状
これが円筒になっても同じ計算方法で温度分布が求まります。
いずれも端点の温度は左側$T_{2}$、右側$T_{1}$とし、周辺温度は$T_{\infty}$とします。周辺温度は実際の外気温と考えれば良いです(だいたい20℃くらい)。
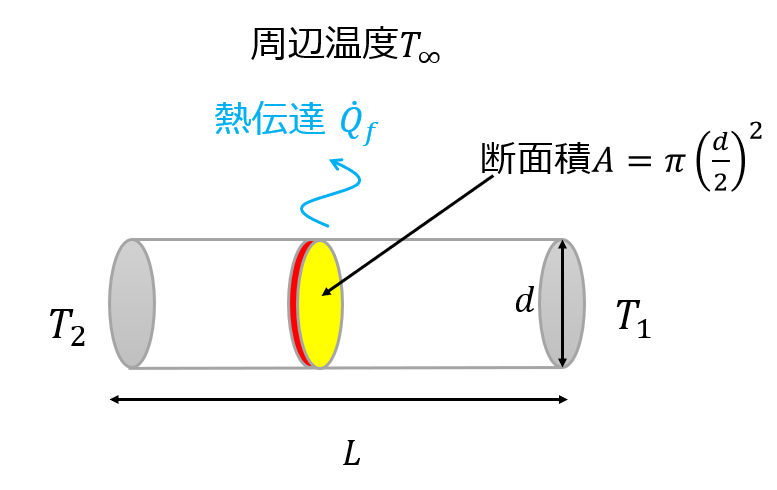
さらに固体壁と周辺の空気との対流熱伝達も考慮して計算を行うことにします。
以上のような状態の時に温度分布がどのようになるのかを理論的に求めたいと思います。
拡大伝熱面の意義
固体壁と流体との熱伝達における伝熱量は$\dot{Q}=hA\Delta T$のように面積に比例します。つまり、伝熱面積$A$を大きくすると伝熱量を大きくすることができます。
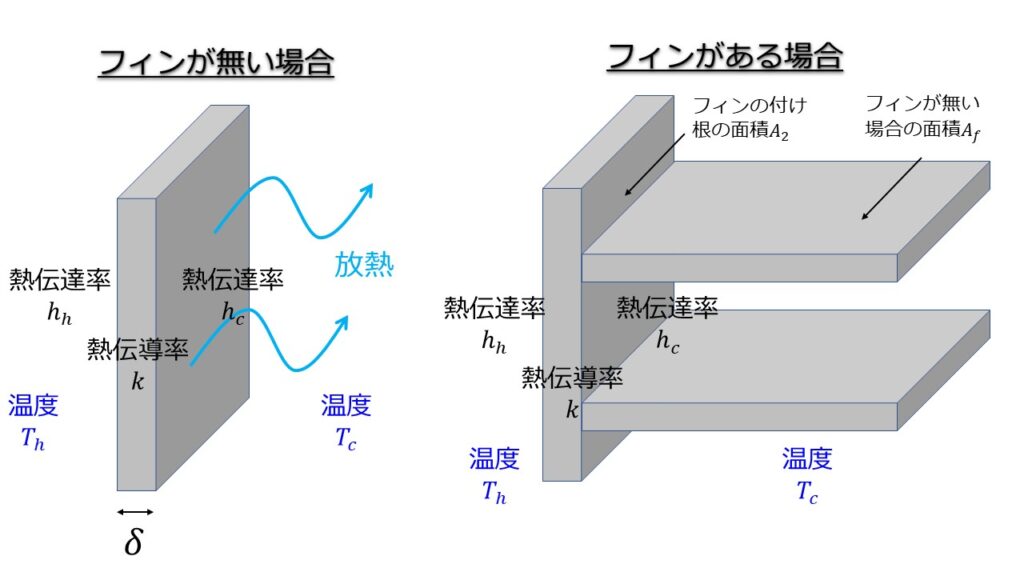
フィンがあることでフィンの側面積$A_{f}$の部分での伝熱量を増やすことができます。
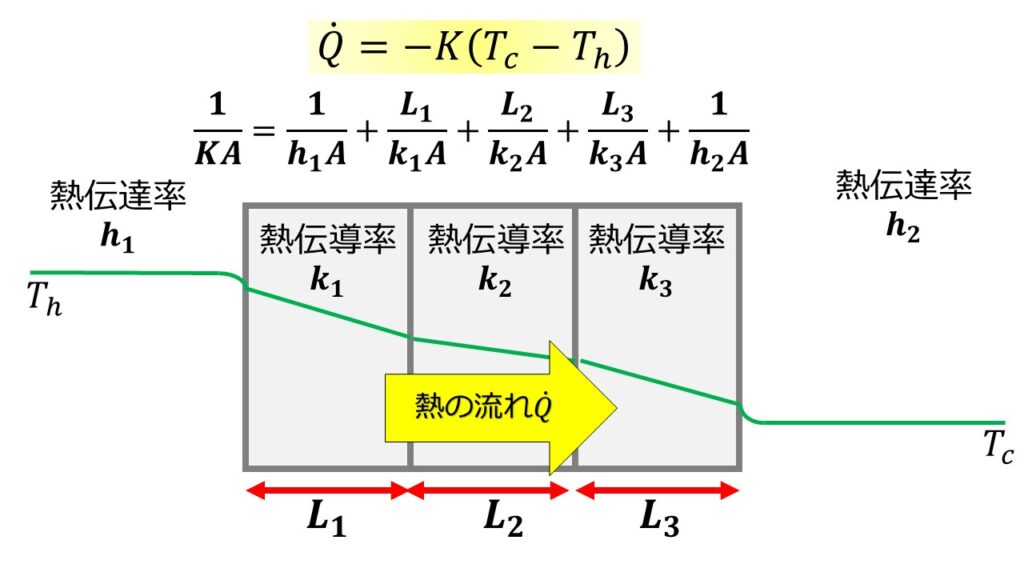
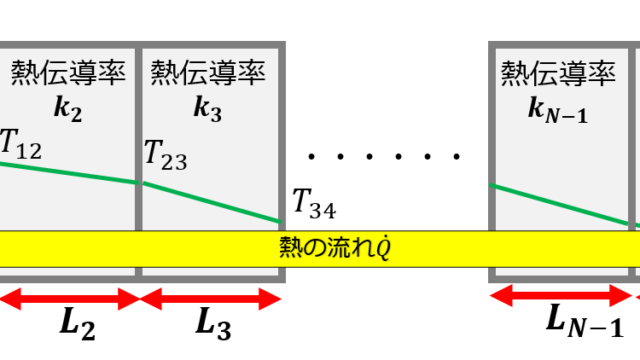
フィンが無い場合の熱伝達（固体と流体）と熱伝導（固体の熱移動）は総括熱伝達係数として以下のように書くことができます。以下の図は例として熱伝導率が異なる3つの物質を連結させた場合の例です。
電気抵抗のように$R=\frac{1}{hA}$とおけば直列回路の合成抵抗のような式になっています。
今回のフィンが無い場合は以下のようになります。
ではフィンが無い場合とある場合で伝熱量の式を見てみましょう。
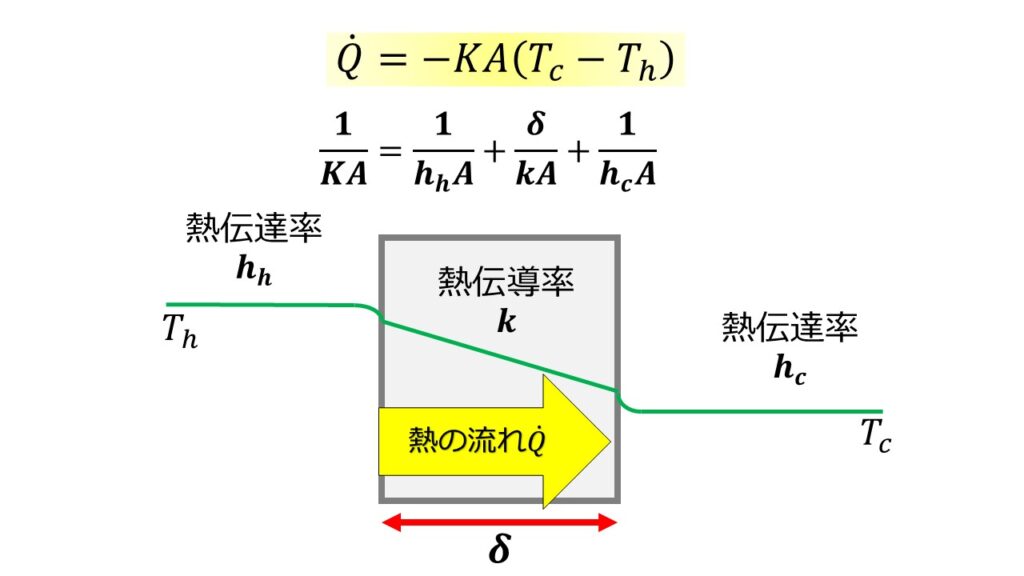
フィンが無い場合の伝熱量
以上の総括熱伝達係数を使うとフィンが無い場合の伝熱量は、
\dot{Q}=\frac{T_{h}-T_{c}}{\frac{1}{h_{h}A}+\frac{\delta}{\lambda}+\frac{1}{h_{c}A}}
\end{align*}
となります。
フィンがある場合の伝熱量
総括熱伝達係数を使うとフィンが無い場合の伝熱量は、
\dot{Q}=\frac{T_{h}-T_{c}}{\frac{1}{h_{h}A}+\frac{\delta}{\lambda}+\frac{1}{h_{c}}\big(\frac{1}{A_{2}+A_{f}}\big)}
\end{align*}
となります。
$A_{f}$を大きくとることで伝熱量を大きくすることができます。熱を上手く逃がして発熱を防ぐことができるということです。
実際はフィンの面積の増加の分、伝熱量が増加するわけではなく、フィン効率$\eta$を用いて以下のように定義されます。
\dot{Q}=\frac{T_{h}-T_{c}}{\frac{1}{h_{h}A}+\frac{\delta}{\lambda}+\frac{1}{h_{c}}\big(\frac{1}{A_{2}+\eta A_{f}}\big)}
\end{align*}
本記事ではフィンからの熱伝達による放熱も考慮してフィンの温度分布を理論的に求めたいと思います。
断面積が一様なフィンの温度分布
熱の収支
形状がシンプルである場合は手計算で求めることができますので、早速計算をしてみましょう。まずは、以下のように微小長さ$dx$における熱の収支を考えることにします。
熱の伝わり方は2種類あります。
- 熱伝導
フーリエの法則：$\dot{q}=-k\frac{dT}{dx}$
熱伝導率：$k[W/m K]$ - 対流熱伝達
フーリエの冷却法則：$\dot{q}=-h\big(T_{\infty}-T\big)$
熱伝達率：$h[W/m^2 K]$
今回は自然対流と考えて良いでしょう。
いつも「式の符号はマイナスがいるのかな？」「どちらの温度からどちらの温度を引けばよかったかな？」と迷う方がいるかもしれませんね。
その場合は、いつも以下のルールに従って立式すれば間違うことはありません。
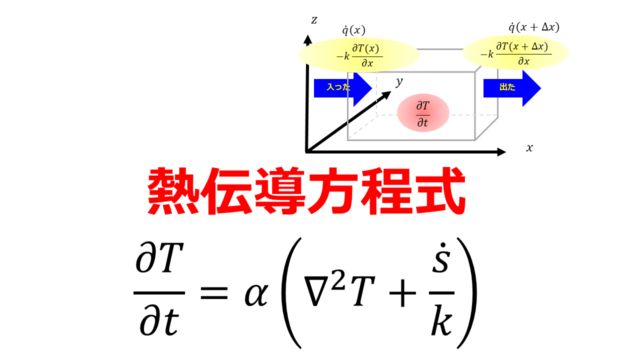
以下の絵は熱伝導の例ですが、対流熱伝達の場合でも同じ考え方が適用できます。
では、ここから式を立てますがまずは熱伝導から考えます。
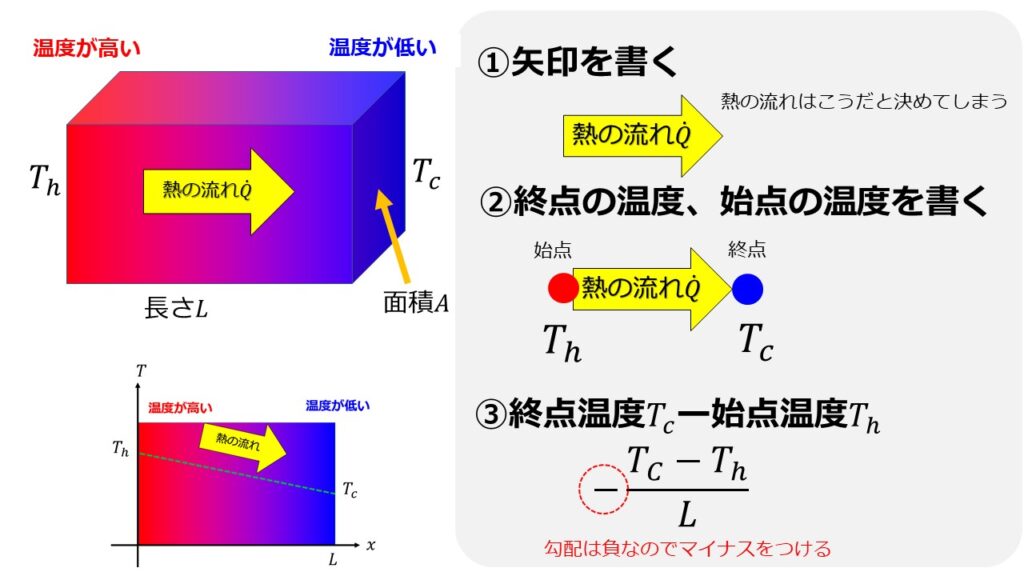
$x$の位置での
- 流入の熱流束：$\dot{Q}(x)$
- 流出の熱流束：$\dot{Q}(x+dx)=\dot{Q}(x)+\frac{d\dot{Q}(x)}{dx}dx$
テーラー展開の1次の項まで残します。
続いて$x$の位置での対流熱伝達は、
- 流出の熱流束：$\dot{Q}_{f}(x)$
となります。
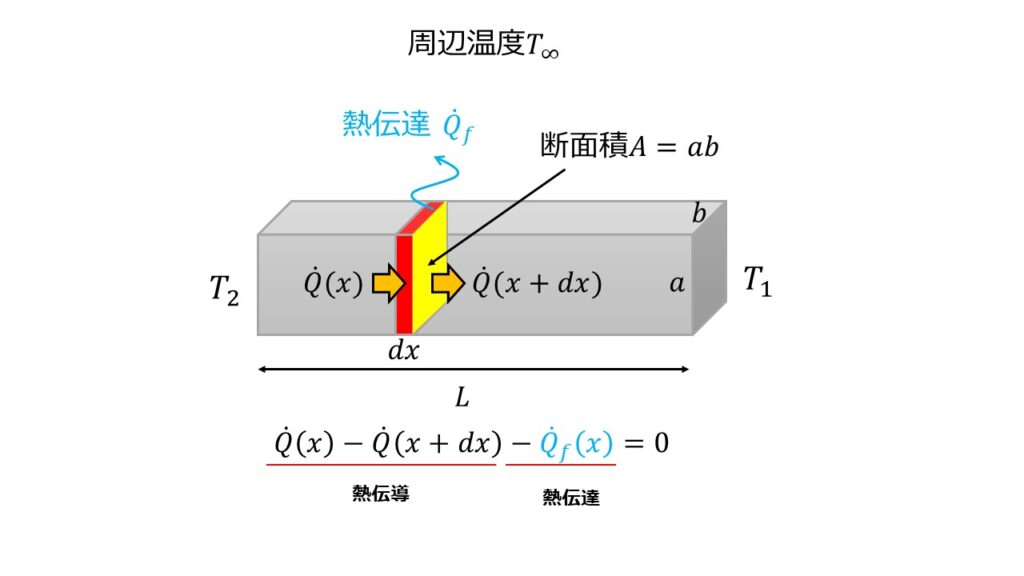
熱の収支を考えると入ってきた熱流束は出ていった熱流束とつりあうので、
\dot{Q}(x)-\dot{Q}(x+dx)-\dot{Q}_{f}(x)=0\tag{1}
\end{align*}
第二項をテーラー展開した形で書いて式を整理すると以下のようになります。
\dot{Q}(x)-\bigg(\dot{Q}(x)+\frac{d\dot{Q}(x)}{dx}dx\bigg)-\dot{Q}_{f}(x)&=0\\
-\frac{d\dot{Q}(x)}{dx}-\dot{Q}_{f}&=0\tag{2}
\end{align*}
そして、
- 第一項でフーリエの法則：$\dot{q}=-k\frac{dT}{dx}$
- 第二項でフーリエの冷却法則：$\dot{q}=-h\big(T-T_{\infty}\big)$
を適用します。
それぞれ$\dot{q}$は単位面積当たりであることに注意する必要があります。
ここからの計算は「立方体形状」でも「円筒形状」でも以下の断面積と周長を置き換えることでどちらでも適用することができるので参考にしてください。
| 断面積 | 側面の周長 | |
| 立方体形状 | $A=ab$ | $l=2(a+b)$ |
| 円筒形状 | $A=\pi\big(\frac{d}{2}\big)^2$ | $l=\pi d$ |
-\frac{d}{dx}\big(-kA\frac{dT}{dx}dx\big)-\bigg(-h\,l dx\big(T_{\infty}-T\big)\bigg)=0\tag{3}
\end{align*}
これを整理すると、
\frac{d^2T}{dx^2}=\frac{hl}{kA}(T-T_{\infty})\tag{4}
\end{align*}
ここで式を見やすくするために、$m^2=\frac{hl}{kA}$、$\theta=\frac{T-T_{\infty}}{T_{2}-T_{\infty}}$と置いて$\theta$に関する微分方程式を得ます。
\frac{d^2\theta}{dx^2}=m\theta\tag{5}
\end{align*}
微分方程式を解く
\frac{d^2\theta}{dx^2}=m\theta\tag{5}
\end{align*}
こちらはバネの振動$\frac{d^2x}{dt^2}=-\frac{k}{m}x$と同じ形をしています。
(5)の一般解は有名なので導出は省くとして以下のようになります。
\theta(x)=C_{1}e^{mx}+C_{2}e^{-mx}\tag{6}
\end{align*}
ここで以下の境界条件
\left\{\begin{matrix}
T=T_{2} &(x=0) \\
T=T_{1} & (x=L)
\end{matrix}\right.
\end{align*}
を課すと、
\left\{\begin{matrix}
\theta(0)&=C_{1}+C_{2}=\frac{T_{2}-T_{\infty}}{T_{2}-T_{\infty}}=1\\
\theta(L)&=C_{1}e^{mL}+C_{2}e^{-mL}=\frac{T_{1}-T_{\infty}}{T_{2}-T_{\infty}}
\end{matrix}\right.
\end{align*}
連立方程式を解くと、
\left\{\begin{matrix}
C_{2}&=\frac{e^{mL}-\frac{T_{1}-T_{\infty}}{T_{2}-T_{\infty}}}{e^{mL}-e^{-mL}}\\
C_{1}&=1-C_{2}
\end{matrix}\right.
\end{align*}
と求まります。
まとめると、
温度に戻したい場合は$T(x)=(T_{2}-T_{\infty})\theta (x) + T_{\infty}$とすれば良いですね。
今までの流れから立方体形状でも円筒形状でも$m$の値が異なるだけで同じ形の式で書くことができます。
- 立方体形状：$m=\frac{h\times 2(a+b)}{k\,ab}$
- 円筒形状：$m=\frac{h\times \pi d}{k\,\pi\big(\frac{d}{2}\big)^2}$
境界条件を課すことで温度分布を得ることができたので、次は具体的な数値を代入して計算してみることにしましょう。
断面積が一様なフィンの温度分布（具体的な値）
- $L=1000$[mm]
- $a=20$[mm]
- $b=30$[mm]
- 熱伝導率：$k=40$[W/m K]
- 熱伝達率：$h=10$[W/m2 K]
- $T_{1}=20$[℃]
- $T_{2}=50$[℃]
- 周辺温度：$T_{\infty}=20$[℃]
Pythonでコードを書きます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 | import numpy as np import matplotlib.pyplot as plt # 長さ Length = 1000 / 1000 # 立方体形状 a = 20 / 1000 b = 30 / 1000 Area_a = a * b l_a = 2*(a+b) # 円筒形状 d = 4/1000 Area_d = np.pi * (d/2)**2 l_d = np.pi * d k = 40 #熱伝達率[W/m K] h = 10 #熱伝達率[W/m2 K] T2 = 50 + 273 #左端温度 T1 = 20 + 273 #右端温度 Tinf = 20 + 273 #周辺温度 x = np.linspace(0, Length, 100) theta = np.empty_like(x) temp = np.zeros_like(x) def temp_func(l, Area,h): m = np.sqrt((h*l)/(k*Area)) c = (T1-Tinf)/(T2-Tinf) c2 = (np.exp(m*Length)- c ) / (np.exp(m*Length)-np.exp(-m*Length)) c1 = 1 -c2 theta = c1 * np.exp(m*x) + c2 * np.exp(-m*x) temp = (T2-Tinf)*theta + Tinf return temp |
グラフを欠いてみましょう。
1 2 3 4 5 6 | temp = temp_func(l_a, Area_a, h) plt.plot(x, temp, label=f'{h}[W/m2 K]') plt.grid() plt.xlabel('x[m]') plt.ylabel('Temp[K]') plt.legend() |
熱伝達は流れによるためパラメータとしていくつか振ってみましょう。
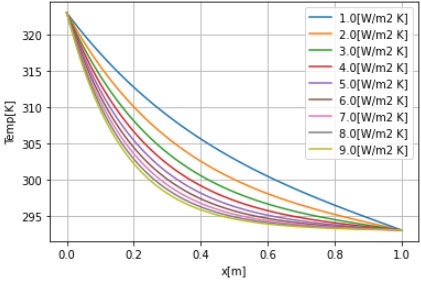
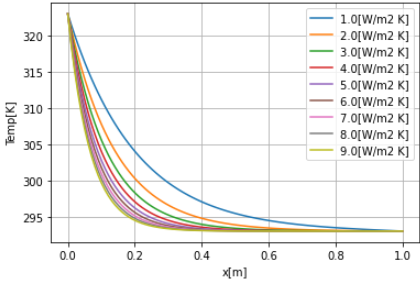
1 2 3 4 5 6 7 8 | h_list = np.arange(1.0,10.0,1.0) #熱伝達をパラメータにする for h_i in h_list: temp = temp_func(l_a, Area_a, h_i) plt.plot(x, temp, label=f'{h_i}[W/m2 K]') plt.grid() plt.xlabel('x[m]') plt.ylabel('Temp[K]') plt.legend() |
熱伝達率を変えることで結構結果が変わりますね。
今度は円筒形状で温度分布を見てみましょう。
今回も熱伝達率をパラメータにします。temp_funcの引数を円筒形状の「側面の周長」と「断面積」に変えるだけですね。
1 2 3 4 5 6 7 8 9 | # 円筒形状 h_list = np.arange(1.0,10.0,1.0) #熱伝達をパラメータにする for h_i in h_list: temp = temp_func(l_d, Area_d, h_i) plt.plot(x, temp, label=f'{h_i}[W/m2 K]') plt.grid() plt.xlabel('x[m]') plt.ylabel('Temp[K]') plt.legend() |
まとめ
今回は断面積が一様なフィンの温度分布の計算方法をまとめました。
$\theta=\frac{T-T_{\infty}}{T_{2}-T_{\infty}}$と置くと$\frac{d^2\theta}{dx^2}=m\theta$
※$m^2=\frac{hl}{kA}$
一般解は、$\theta(x)=C_{1}e^{mx}+C_{2}e^{-mx}$となります。
※境界条件は問題設定によります。
温度に戻したい場合は$T(x)=(T_{2}-T_{\infty})\theta (x) + T_{\infty}$とすれば良いですね。
左側だけを温度規定した場合は右側は温度勾配が0($\dot{Q}=-kA\frac{dT}{dx}=0$)の断熱とした境界条件を課して解を求めるのが良いでしょう。
\left\{\begin{matrix}
T=T_{2} &(x=0) \\
\frac{dT}{dx}=0 & (x=L)
\end{matrix}\right.
\end{align*}
参考書
実用的な内容も多く伝熱工学の基礎から解説をしている以下の参考書がお勧めです。
Follow @t_kun_kamakiri