こんにちは(@t_kun_kamakiri)
本記事では熱ひずみと熱応力について具体的な計算方法も合わせて解説を行います。
物体に熱を加えて温度変化すると、加えた温度に応じて膨張する現象を熱膨張といい、熱膨張に関する製品不具合を回避するための設計のことを熱設計と呼んだりするくらい重要な問題です。
熱設計に強くなるためには熱によって生じる熱ひずみと、熱ひずみによって生じる熱応力の基礎的な理論を押さえておく必要があります。本記事では、以下の内容をまとめています。
- 熱ひずみと熱応力とは
- 熱応力の具体的な計算方法の手順を知りたい方
自分自身が機械設計をする際には熱ひずみ(または熱変位)を意識する必要があり、熱に対する問題はとても大きいです。また、技術士1次試験の機械部門でも必ず出題される問題で機械設計者には切っても切れない関係でしょう。
本記事は、熱ひずみと熱応力をこれから学ぼうとしている方や技術士の1次試験対策をしている方などに向けて書いています。具体的な計算方法を示しながら解説を行いたいと思います。
- 熱ひずみと熱応力の基礎を学びたい方
- 技術士1次試験に出題する熱ひずみと熱応力の対策をしたい方
- 熱設計でお困りの方(製造業関係者)
熱ひずみとは
物体は温度変化によって膨張(または収縮)します。つまり物体が温まると伸びたり(または縮んだり)するということです。
問題を簡単にするために1次元で考えることにします。長さ$L$の物体が、温度$\Delta T$℃上昇したときの伸びを$\Delta L$とすると以下の式で表すことができます。
物体が温度変化したことと膨張したことを結びつける係数$\alpha$を導入すると、
\Delta L= \alpha L \Delta T\tag{1}
\end{align*}
という関係で表すことができます。ここで、単位長さあたりの伸び$\varepsilon_{t} = \frac{L}{\Delta L}$を導入すると、
\varepsilon_{t} = \alpha \Delta T\tag{2}
\end{align*}
と書くことができます。$\varepsilon_{t}$が熱ひずみです。
単位長さ当たりの伸ずのことを材料力学の用語でひずみといいますが、それが熱によって生じているため熱ひずみという言うわけですね。
ここで導入した$\alpha$を線膨張係数といいます。
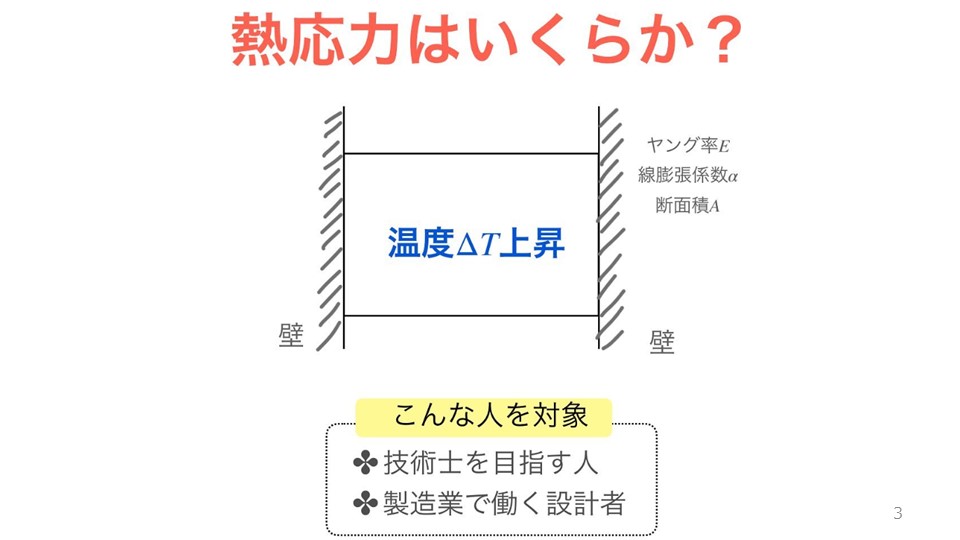
熱応力とは
もし、物体の温度上昇によって熱ひずみが発生したとしても物体が自由に膨張できる場合は熱応力が発生しませんが、多くの機械は固定部分があったり、異なる熱膨張係数どうしで結合していたりしています。ゆえに、自由に膨張できるというわけではなく、動きが制限されているため内部で応力が発生します。
それが熱応力です。
例えば以下のように長さ$L$の物体が両端固定された状態で温度上昇$\Delta T$したとします。
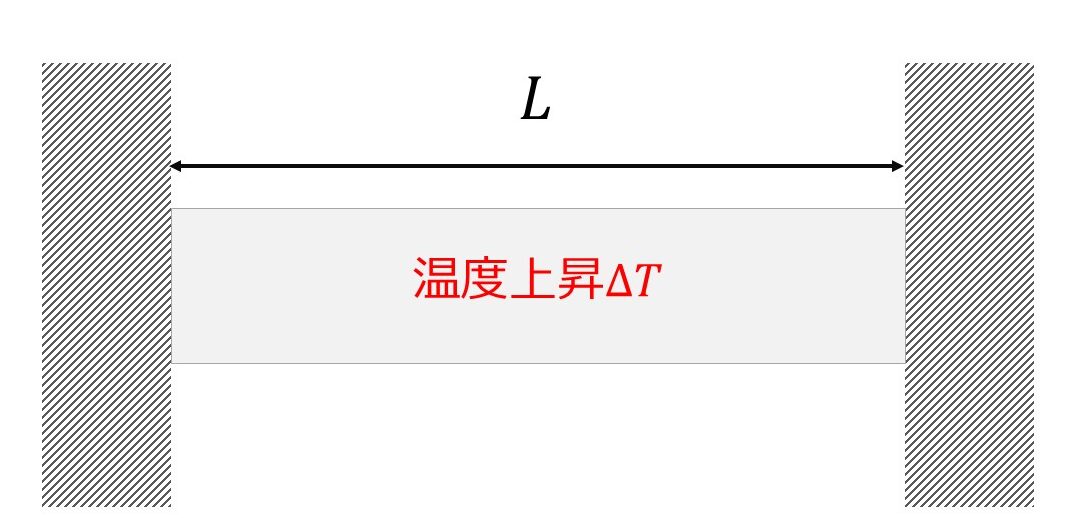
もし右側の固定部分がなければ物体は自由に膨張できるため熱膨張します。
- 熱膨張係数$\alpha[K^{-1}]$
- ヤング率$E [N/m^2]$

この場合は「熱ひずみ」で解説した単位長さあたりの伸び$\varepsilon_{t} = \frac{L}{\Delta L}$により$\varepsilon_{t} = \alpha \Delta T$の熱ひずみが生じることになります。
しかし、実際は右側は固定されているため物体が温度上昇に伴って伸びようとした分を阻止するように圧縮の応力が作用します。このとき、フックの法則$\sigma = E\varepsilon $により、ひずみは
\varepsilon = \frac{\sigma}{E}\tag{3}
\end{align*}
となります。
熱膨張によって熱ひずみが生じましたが、そのひずみをなくす方向の圧縮応力が生じているということです。
- 熱膨張による熱ひずみ:$\varepsilon_{t} = \alpha \Delta T$
- 膨張を圧縮する方向の伸び:$\varepsilon = \frac{\sigma}{E}$
物体は両端で固定されているため全体の伸びは0ということを考慮すると
\underset{熱ひずみ}{\varepsilon_{t}} +\underset{圧縮ひずみ}{\varepsilon} =0\\
&\Leftrightarrow\\
\alpha \Delta T+\frac{\sigma}{E} =0\\
&\Leftrightarrow\\
\sigma = -E\alpha\Delta T
\end{align*}
この$\sigma = -E\alpha\Delta T$が熱によって膨張した内部応力で熱応力です。
本来、引張り応力を正の方向としているため、圧縮である場合のフックの法則は$-\sigma = E\varepsilon $のように書く方が良いかもしれませんが、力の正負は力の方向を意味するため、何も気にせずにフックの法則$\sigma = E\varepsilon $を使うのが良いです。なぜなら、求めた$\sigma$がマイナスであれば圧縮だと解釈すれば良いので、立式する際には引張りか圧縮かを気にせずに全て引張りを正とした$\sigma = E\varepsilon $を使えば良いでしょう。
熱応力解析とは
実物のモノで熱設計を行う場合は今回のような単純形状ではないため、手計算で求めることは困難です。そうしたときには、モデル内で温度条件を与えることで、温度分布を知ることができます。
そして、物体の境界条件を与え温度分布を参照することで物体に生じる熱応力を計算することができます。このような解析を熱-構造解析といいます。
まとめ
今回は熱ひずみと熱応力の基本的な内容を解説しました。
熱膨張によって生じるひずみが熱ひずみ。その熱ひずみによって物体が自由に動けない場合に生じる応力が熱応力です。
参考書
技術士1次試験の問題は過去問+解説付きのこちらの参考書をきっちりやり込めば問題ありません。
材料力学の参考書としては以下の2冊を手元に置いて置けば良いでしょう。