こんにちは（@t_kun_kamakiri）(‘◇’)ゞ
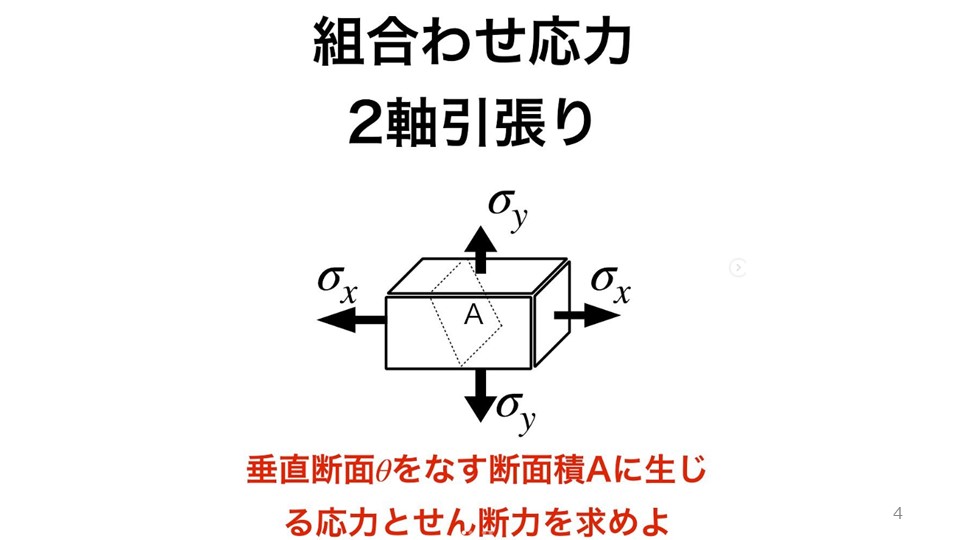
2軸引張りとせん断力による組み合わせ応力は、
\begin{align*}
\sigma &= \frac{\sigma_{x}+\sigma_{y}}{2}+\frac{\sigma_{x}-\sigma_{y}}{2}\cos 2\theta + \tau_{xy}\sin 2\theta\tag{1}\\
\tau &= \frac{\sigma_{x}-\sigma_{y}}{2}\sin 2\theta + \tau_{xy}\cos 2\theta\tag{2}
\end{align*}
\sigma &= \frac{\sigma_{x}+\sigma_{y}}{2}+\frac{\sigma_{x}-\sigma_{y}}{2}\cos 2\theta + \tau_{xy}\sin 2\theta\tag{1}\\
\tau &= \frac{\sigma_{x}-\sigma_{y}}{2}\sin 2\theta + \tau_{xy}\cos 2\theta\tag{2}
\end{align*}
となります。
(1)と(2)を使ってモールの応力円と呼ばれる式を使って、で物体の応力状態を図示することができます。
\begin{align*}
\bigg(\sigma-\frac{\sigma_{x}-\sigma_{y}}{2}\bigg)^2 + \tau^2 = \bigg(\frac{\sigma_{x}-\sigma_{y}}{2}\bigg)^2+\tau_{xy}^2\tag{3}
\end{align*}
\bigg(\sigma-\frac{\sigma_{x}-\sigma_{y}}{2}\bigg)^2 + \tau^2 = \bigg(\frac{\sigma_{x}-\sigma_{y}}{2}\bigg)^2+\tau_{xy}^2\tag{3}
\end{align*}
(3)は中心$\big(\frac{\sigma_{x}-\sigma_{y}}{2}, 0\big)$、半径$\sqrt{\big(\frac{\sigma_{x}-\sigma_{y}}{2}\big)^2+\tau_{xy}^2}$の円の方程式となります。
Follow @t_kun_kamakiri