有限体積法

1次元熱拡散方程式（熱伝導方程式）の有限体積法を解説(1)

こんにちは（@t_kun_kamakiri）

本記事では流体解析の離散化である有限体積法について基礎的な解説を行います。

有限体積法はOpenFOAMなど流体解析でも使われる離散化の方法です。流体解析用ソフトの多くが有限体積法を採用しており、人によってはプログラムを実装したことがないがために有限体積法のイメージが付かないという方も多いかと思います。

有限体積法のわかりやすい解説記事もなかなかないため、自身で勉強したことをわかりやすく解説する記事を残しておこうと思っています。

本記事の内容
  • 熱拡散方程式を有限体積法で離散化
  • 有限体積法を手計算で導出する

流体力学の基礎方程式のひとつである運動量保存則を数値的に取り扱う際の離散化方法のひとつが有限体積法です。有限体積法は領域をコントロールボリューム(以下CV)という領域で離散化して、数値的に解く手法です。

ナビエストークス方程式をいきなり扱って有限体積法を理解するのはハードルが高いでしょう。そこで、本記事では有限体積法の基礎を学ぶために、熱拡散方程式（熱伝導方程式とも呼ぶ）である以下の式を手計算で体験してみます。

\begin{align*}
\rho c\frac{\partial T}{\partial t} = \frac{\partial}{\partial x}\bigg(k\frac{\partial T}{\partial x}\bigg)\tag{1}
\end{align*}

熱拡散方程式は初期温度分布から時間が経つと高温から低温に温度が拡散するモデル式です。

あわせて読みたい

【1次元熱伝導方程式】Fortranからgnuplotでグラフの１次元アニメーション作成

いきなり難しいことを学ばずに、基礎固めをしっかりすることで楽しく学び続けることができるでしょう。

こんな方が対象
  • 数値流体の有限体積法の基礎を学びたい方
  • OpenFOAMで使われる有限体積法を学びたい方

最終的には流体の基礎方程式であるナビエストークス方程式をC++実装する解説記事やOpenFOAMでの解説記事を書きたいと思います。

C++を使った差分法の記事は以下に書きました。
オブジェクト指向を意識したため少々読みづらさはありますが、追加での実装は楽になったと思います。

あわせて読みたい

【オブジェクト指向C++】2次元ナビエストークス方程式(キャビティ流れ)の数値計算

本記事が有限体積法の第一歩として参考になれば幸いです。

目次
  1. 有限体積法とは
  2. 熱拡散方程式の有限体積法
  3. コントロールボリューム内で積分
  4. 有限時間で積分する
  5. 左辺：$\int_{t}^{t+\Delta t}\left [\int_{CV}\frac{\partial T}{\partial t}\,dV\, \right ]\,dt$
  6. 右辺：$\int_{t}^{t+\Delta t}\left [ \bigg(DA\frac{\partial T}{\partial x}\bigg)_{e}-\bigg(DA\frac{\partial T}{\partial x}\bigg)_{w}\right ]\, dt$
    1. 空間微分の離散化：$\frac{\partial T}{\partial x}$の空間微分をどのように表現するか？
    2. 時間積分：$\big(DA\frac{\partial T}{\partial x}\big)_{w}$や$\big(DA\frac{\partial T}{\partial x}\big)_{e}$をどの時間の$T$を使うか？
    3. 一般的な時間積分の形
  7. 空間微分の離散化と時間積分
  8. 境界での離散化の式
  9. 行列にまとめる
  10. まとめ
  11. 参考書

有限体積法とは

有限体積法(finite volume method＝FVMと略)は偏微分方程式の局所的な保存性に基づく離散化手法です。

以下のように計算領域をコントロールボリューム(以下CVと略）と呼ばれる領域に分けて各CVで積分を行い、流体の基礎式の移流項や拡散項はガウスの発散定理を利用してCVからの正味の流出量に書き直します。

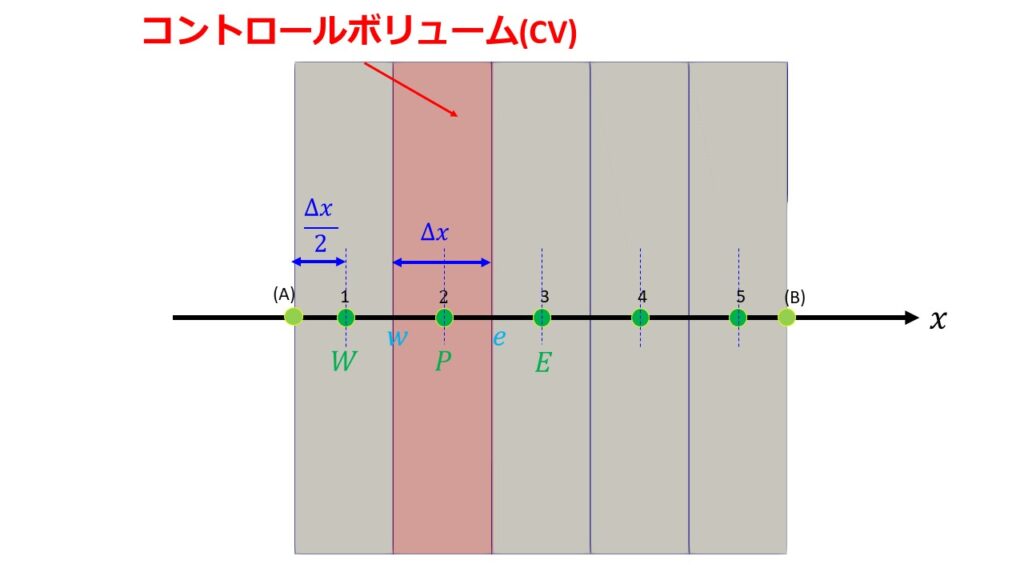
有限体積法は、差分法に比べて計算領域の形状に対する自由度が高く境界条件の扱いも容易であるため流体解析の離散化手法としてもよく用いられています。

熱拡散方程式の有限体積法

$k,c$は定数として、$D=\frac{k}{\rho c}$と置くことにより、

\begin{align*}
\frac{\partial T}{\partial t} = \frac{\partial}{\partial x}\bigg(D\frac{\partial T}{\partial x}\bigg)\tag{2}
\end{align*}

となります。

$D$は場所によって変わる場合もあります。ゆえに、微分の中に$D$を入れていた方が一般的な形ですが、本記事では有限体積法の基礎を理解することを目的としているため、後ほど具体的な値を用いて計算するときには$D$は一定値として扱います。

CV内での離散化を行うまでは、$D$は微分の中に入れたまま進めます。$D$が定数の場合は、微分の外に出せますので$D$が微分の中にあることはあまり気にしなくても良いでしょう。

コントロールボリューム内で積分

今回は有限体積法の基礎を理解するために1次元のコントロールボリューム（以下CV)について考えることにします。
計算領域は離散点1~5の5つとします。
CV内の格子点$P$に着目し、隣の格子点$W$と$E$、CVの界面の点を$w$と$e$とします。格子点$P$での物理量（温度$T$）の時間変化を求めることが目的です。

まずは、(2)においてCV内での積分を考えます。

\begin{align*}
\int_{CV}\frac{\partial T}{\partial t}dV = \int_{CV}\frac{\partial}{\partial x}\bigg(D\frac{\partial T}{\partial x}\bigg)dV\tag{3}
\end{align*}

左辺に対してはガウスの定理を用います。

ガウスの定理

\begin{align*}
\int \nabla \cdot \boldsymbol{F}\,dV = \int \boldsymbol{F}\cdot \boldsymbol{n}\,dS
\end{align*}

ガウスの定理は微小体積の変化量は、微小体積から流出した正味の量と等しいことを意味します。
ガウスの定理に従ってナブラ演算子$\nabla=\big(\frac{\partial }{\partial x},\frac{\partial }{\partial y},\frac{\partial }{\partial z}\big)$を使って展開します。

\begin{align*}
\int \bigg(\frac{\partial F_{x}}{\partial x}+\frac{\partial F_{y}}{\partial y}+\frac{\partial F_{z}}{\partial z}\bigg)dV = \int \big(F_{x}n_{x}+F_{y}n_{y}+F_{z}n_{z}\big)dS
\end{align*}

1次元であることを考慮すると$F_{y}=0,F_{z}=0$であり、$y$と$z$の微分は0になるので以下となります。

\begin{align*}
\int \frac{\partial F_{x}}{\partial x}dV = \int F_{x}n_{x}dS
\end{align*}

※2次元や3次元になるとCVの界面の法線ベクトルと格子間を結ぶベクトルが平行にならないときもあるため、上記の式のようにきれいな形にはなりません。今回は、CVの界面の法線ベクトルと格子間を結ぶベクトルが平行の場合であることに注意します。

そして左辺はCVの界面$w$と$e$から流出した正味の量ということになります。

$D\frac{\partial T}{\partial x}=F$と置けば、

\begin{align*}
\int_{CV}\frac{\partial }{\partial x}\bigg(D\frac{\partial T}{\partial x}\bigg)dV &= \int \bigg(D\frac{\partial T}{\partial x}n_{x}\bigg)dS\\
&=\bigg(DA\frac{\partial T}{\partial x}\bigg)_{e}-\bigg(DA\frac{\partial T}{\partial x}\bigg)_{w}\tag{4}
\end{align*}

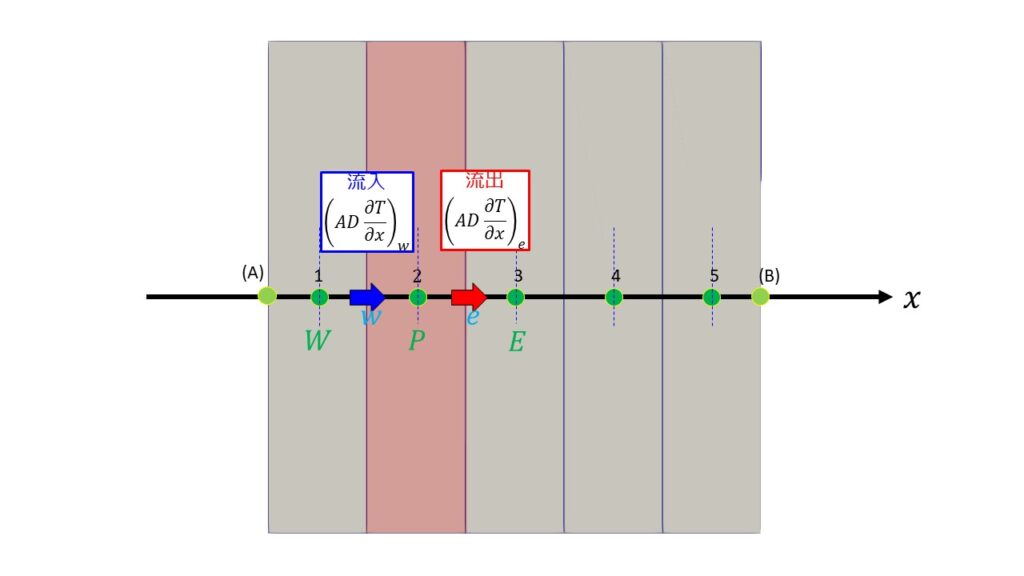
  • $P$：CVの中心の格子点
  • $W$：隣の西側（左側）の格子点
  • $E$：隣の東側（右側）の格子点
  • $w$：CV界面西側（左側）の格子点
  • $e$：CV界面東側（右側）の格子点
  • $A$：CV界面の面積

そして出てきた1階微分の$\frac{\partial T}{\partial x}$をどのように離散化するかがカギになります。

ガウスの定理を使ったCV内での式は以下となります。

\begin{align*}
\int_{CV}\frac{\partial T}{\partial t}dV = \bigg(DA\frac{\partial T}{\partial x}\bigg)_{e}-\bigg(DA\frac{\partial T}{\partial x}\bigg)_{w}\tag{5}
\end{align*}

有限時間で積分する

時間変化する非定常問題において有限時間$\Delta t$で積分をする必要があります。

\begin{align*}
\int_{t}^{t+\Delta t}\left [\int_{CV}\frac{\partial T}{\partial t}\,dV\, \right ]\,dt=\int_{t}^{t+\Delta t}\left [ \bigg(DA\frac{\partial T}{\partial x}\bigg)_{e}-\bigg(DA\frac{\partial T}{\partial x}\bigg)_{w}\right ]\, dt\tag{6}
\end{align*}

左辺と右辺をひとつずつ見ていきましょう。

左辺：$\int_{t}^{t+\Delta t}\left [\int_{CV}\frac{\partial T}{\partial t}\,dV\, \right ]\,dt$

右辺はCVでの積分はガウスの定理によりCV界面から流出する正味の量に置き換わったために積分はなくなっています。

左辺は有限の値にしかならないため、時間積分と空間積分を入れ替えることができます。
$\int_{t}^{t+\Delta t}\left [\int_{CV}\frac{\partial T}{\partial t}\,dV\, \right ]\,dt=\int_{CV}\left [\int_{t}^{t+\Delta t}\frac{\partial T}{\partial t}\, dt\, \right ]\,dV$

時間についても離散化する必要があります。
格子点$P$における温度の変化を知りたいので、$P$での温度は下付き文字で$T_{P}$と表ことにします。$t+\Delta t$における温度はそのまま$T_{P}$と書き、$t$における温度は$T^{o}_{P}$と表すことにします。
※上付き文字の$o$はoldの略です。
$t+\Delta t$から見ると$t$での値は古い値（old）だからですね。

  • $t+\Delta t$における温度：$T_{P}$
  • $t$における温度：$T^{o}_{P}$

時間微分に関しては$\frac{\partial T}{\partial t}=\frac{T_{P}-T_{P}^{o}}{\Delta t}$と離散化します。これは$\Delta t$が十分小さいとして、$t$~$t+\Delta t$の間は$t$における$T_{P}^{o}$と$t+\Delta t$における$T_{P}$の2点で微分を表現するという近似を行っています。

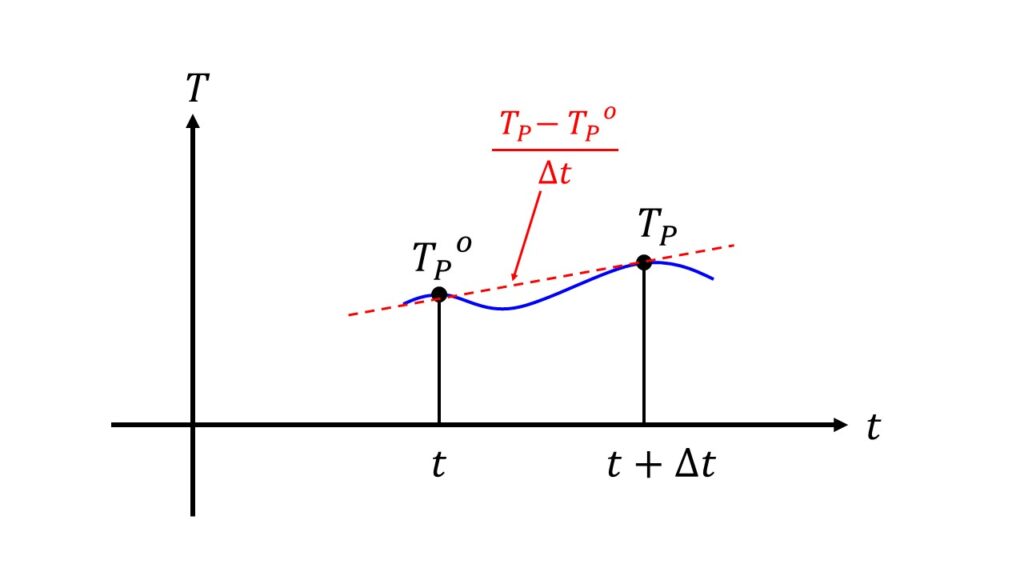
$\int_{t}^{t+\Delta t}\frac{\partial T}{\partial t}\, dt =\int_{t}^{t+\Delta t}\frac{T_{P}-T_{P}^{o}}{\Delta t}\, dt=\frac{T_{P}-T_{P}^{o}}{\Delta t}\Delta t$と書き直します。

さらに$\int_{CV} \,dV = \Delta V$であるため、

\begin{align*}
\int_{t}^{t+\Delta t}\left [\int_{CV}\frac{\partial T}{\partial t}\,dV\, \right ]\,dt = \frac{T_{P}-T_{P}^{o}}{\Delta t}\Delta t \Delta V\tag{7}
\end{align*}

となります。

右辺：$\int_{t}^{t+\Delta t}\left [ \bigg(DA\frac{\partial T}{\partial x}\bigg)_{e}-\bigg(DA\frac{\partial T}{\partial x}\bigg)_{w}\right ]\, dt$

$\int_{t}^{t+\Delta t}\left [ \bigg(DA\frac{\partial T}{\partial x}\bigg)_{e}-\bigg(DA\frac{\partial T}{\partial x}\bigg)_{w}\right ]\, dt$に関しては少々考えなければなりません。

偏微分を数値的に扱うためには格子点を使って離散化する必要があります。

  1. 空間微分の離散化：$\frac{\partial T}{\partial x}$の空間微分をどのように表現するか？
  2. 時間積分：$\big(DA\frac{\partial T}{\partial x}\big)_{w}$や$\big(DA\frac{\partial T}{\partial x}\big)_{e}$をどの時間の$T$を使うか？

この2つの問題に直面します。

では、まず一つ目の問題の「空間微分の離散化」について考えます。

空間微分の離散化：$\frac{\partial T}{\partial x}$の空間微分をどのように表現するか？

まずは$\frac{\partial T}{\partial x}$の空間微分について考えます。

$\big(\frac{\partial T}{\partial x}\big)_{e}$という下付き文字$e$はCVの右側界面での微分を意味します。この微分を離散点で表現する簡単な方法としては両隣のCVの格子点を使った方法があります。

つまり、$\big(DA\frac{\partial T}{\partial x}\big)_{e}=DA\frac{T_{E}-T_{P}}{\Delta x}$となります。

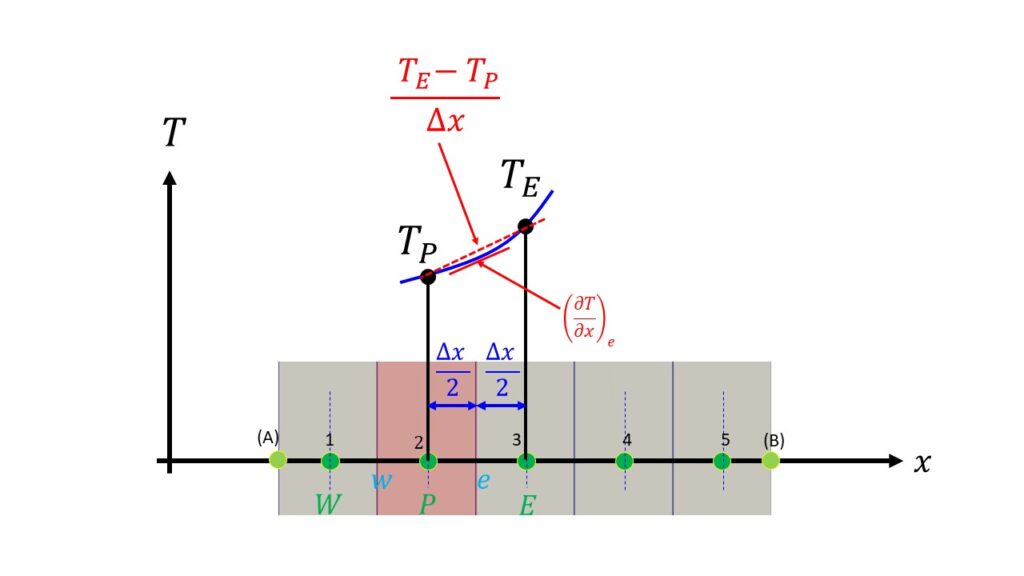
同様に$\big(DA\frac{\partial T}{\partial x}\big)_{w}$についても隣接する2つの格子点を使って表します。
$\big(DA\frac{\partial T}{\partial x}\big)_{w}=DA\frac{T_{P}-T_{W}}{\Delta x}$

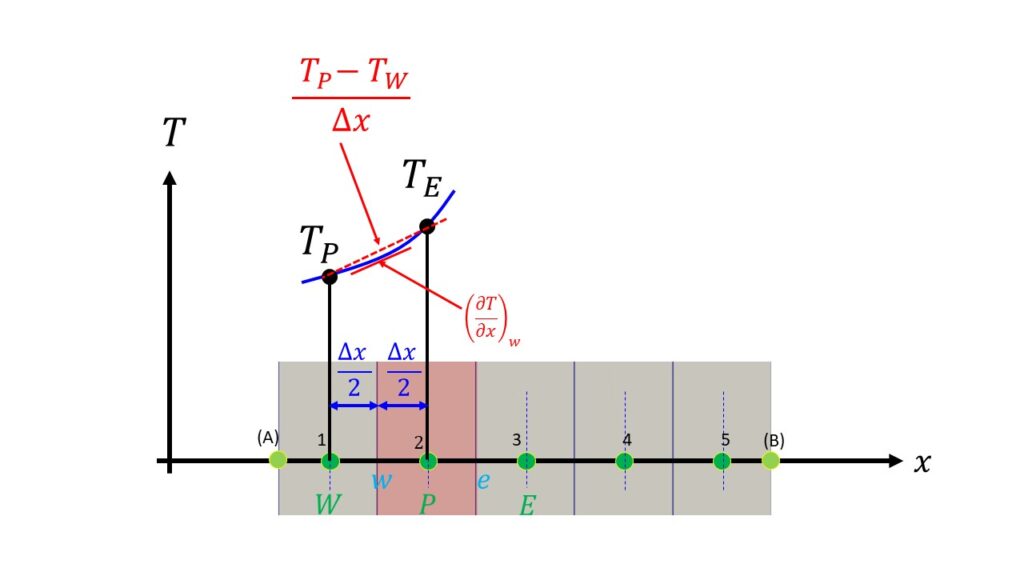
この離散化の方法は隣接する2つの格子点を使って間の微分を表現することから中心差分と呼ばれています。

では(5)の右辺をまとめると、

\begin{align*}
\int_{t}^{t+\Delta t}\left [\int_{CV}\frac{\partial T}{\partial t}\,dV\, \right ]\,dt &=\int_{t}^{t+\Delta t}\left [ \bigg(DA\frac{\partial T}{\partial x}\bigg)_{e}-\bigg(DA\frac{\partial T}{\partial x}\bigg)_{w}\right ]\, dt\\
&=\int_{t}^{t+\Delta t}\left [DA\frac{T_{E}-T_{P}}{\Delta x}-DA\frac{T_{P}-T_{W}}{\Delta x}\right ]\, dt\tag{8}
\end{align*}

となります。
今回は空間微分を中心差分で表現しましたが、前進差分や後退差分など離散化の方法は色々あり、どれも空間微分をテーラー展開した打切り誤差を含むため完ぺきなものはなく、どのように離散化するかによって解の精度や振る舞いが変わります。

中心差分についても精度と解の振る舞いについてはよく考察する必要があるため、次の記事で詳しく解説を行います。

次に時間積分に関する項について考えましょう。

時間積分：$\big(DA\frac{\partial T}{\partial x}\big)_{w}$や$\big(DA\frac{\partial T}{\partial x}\big)_{e}$をどの時間の$T$を使うか？

続いて、時間積分$\big(DA\frac{\partial T}{\partial x}\big)_{w}$や$\big(DA\frac{\partial T}{\partial x}\big)_{e}$をどの時間の$T$を使うか？という問題を考えます。

わかりやすくするために$DA\frac{\partial T}{\partial x}=F$と置いて考えまましょう。

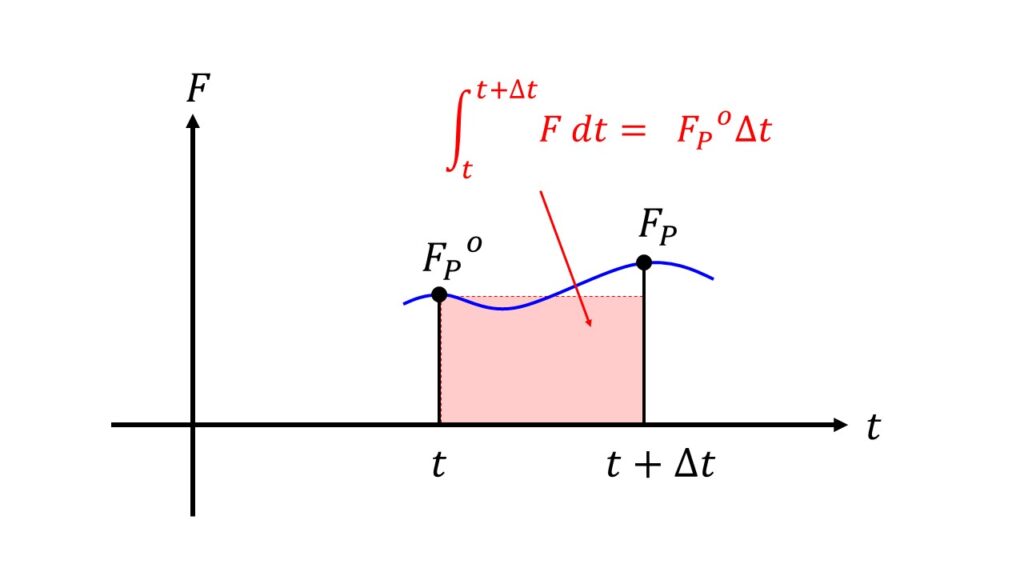
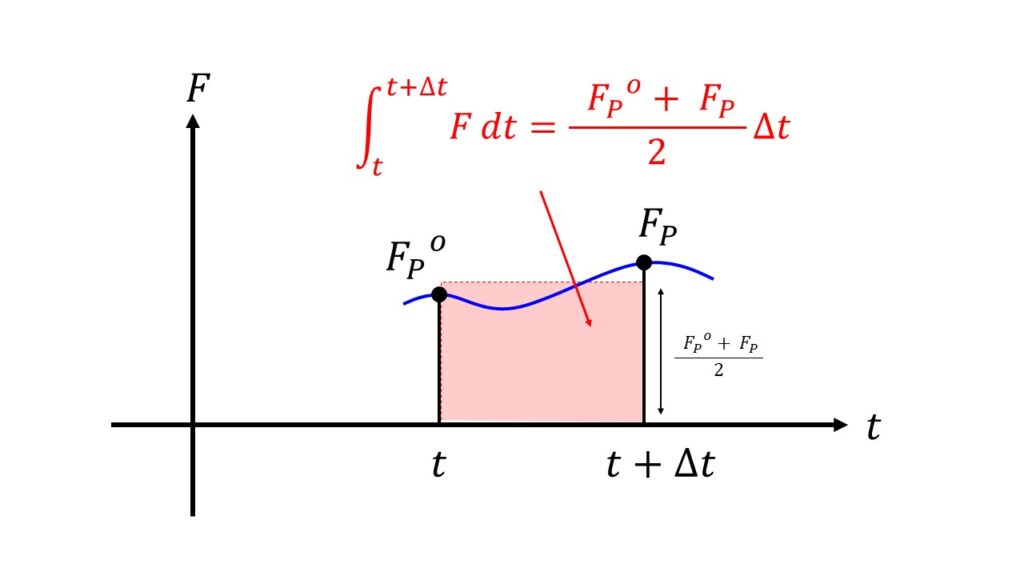
ということは、$\int_{t}^{t+\Delta t}\big(DA\frac{\partial T}{\partial x}\big)\,dt = \int_{t}^{t+\Delta t}F\,dt$を考えることになります。

本当は$t~\Delta t$までの$F(t)$も使って上の絵のように連続的に積分を行いたいのですが、あいにく時間に関しても離散的であるため$t$における$F_{p}^{o}$か$t+\Delta t$における$F_{p}$を使うしかありません。

その方法は色々とありますので以下に列挙します。

１．$t$における$F_{p}^{o}$を使う場合

２．$t+\Delta t$における$F_{p}$を使う場合

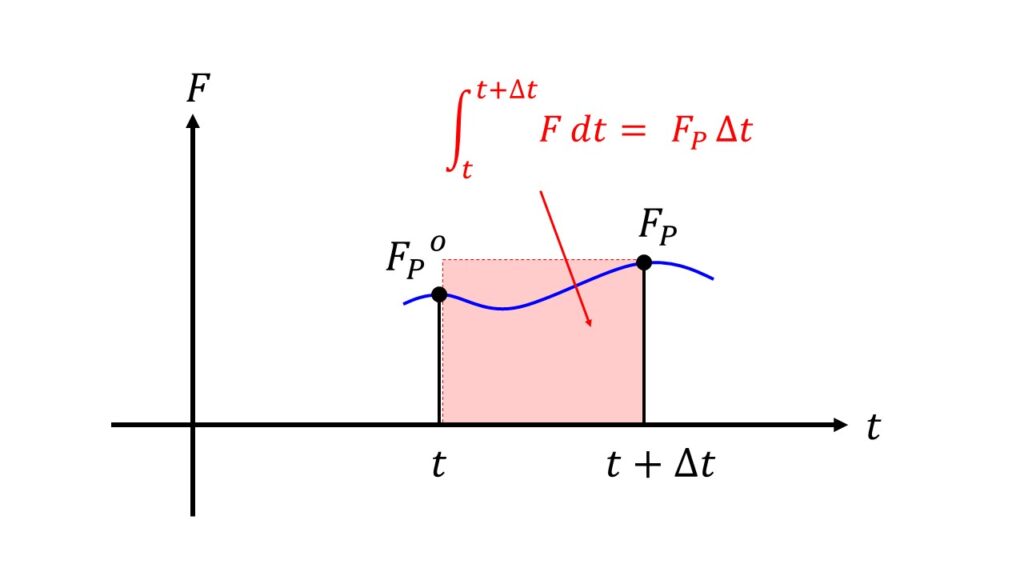
３．$t$における$F_{p}^{o}$と$t+\Delta t$における$F_{p}$を使う場合

以上、

\begin{align*}\int_{t}^{t+\Delta t}\left [\int_{CV}\frac{\partial T}{\partial t}\,dV\, \right ]\,dt=\int_{t}^{t+\Delta t}\left [ \bigg(DA\frac{\partial T}{\partial x}\bigg)_{e}-\bigg(DA\frac{\partial T}{\partial x}\bigg)_{w}\right ]\, dt\end{align*}
の離散化をまとめると以下のようになります。

(6)の離散化時間積分の解法
\begin{align*}\left [\big(F_{P}^{O}\big)_{e}-\big(F_{P}^{O}\big)_{w}\right ]\, \Delta t\end{align*}
陽解法
\begin{align*}\left [\big(F_{P}\big)_{e}-\big(F_{P}\big)_{w}\right ]\, \Delta t\end{align*}
完全陰解法
\begin{align*}\left [\bigg(\frac{F_{P}^{o}+F_{P}}{2}\bigg)_{e}-\bigg(\frac{F_{P}^{o}+F_{P}}{2}\bigg)_{w}\right ]\, \Delta t\end{align*}
陰解法
（クランクニコルソン法）

右辺に$t+\Delta t$における値$F_{P}$を含まない解法を陽解法、右辺に$t+\Delta t$における値$F_{P}$を含む解法を陰解法と呼びます。

一般的な時間積分の形

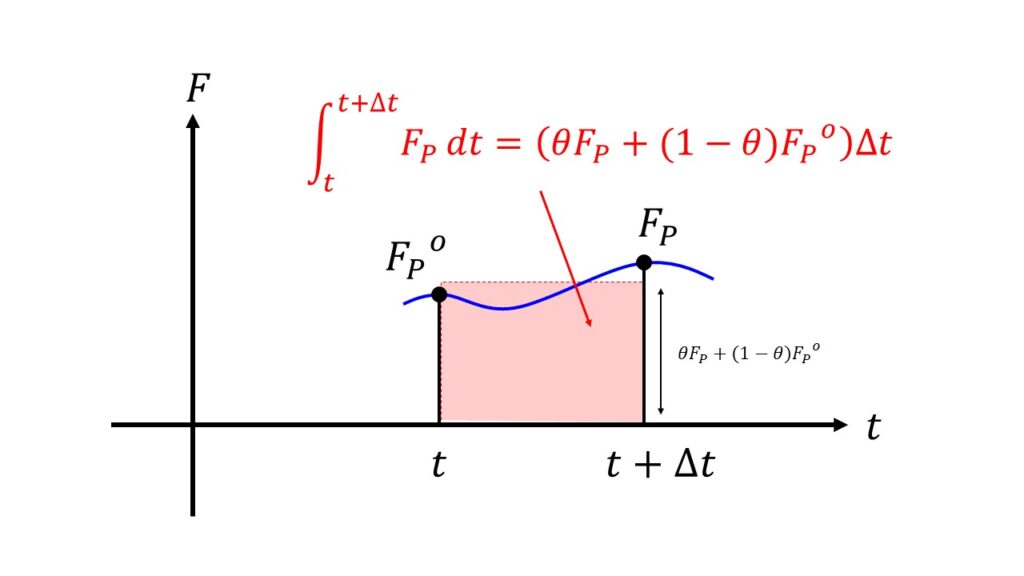
陽解法、陰解法、クランクニコルソン法など時間積分を近似する方法を紹介しました。

下の絵のように、連続する$F(t)$を、

  • $t+\Delta t$での値$F_{P}$の割合を$\theta$
  • $t$での値$F_{P}^{o}$の割合を$1-\theta$

という比率を使って表すことにより一般化した形で表現することができます。

\begin{align*}
\int_{t}^{t+\Delta t}F_{P}(t)\, dt &\simeq \int_{t}^{t+\Delta t}\bigg(\theta F_{P}+(1-\theta)F_{P}^{o}\bigg)\, dt\\
&=\big(\theta F_{P}+(1-\theta)F_{P}^{o}\big)\Delta t\tag{9}
\end{align*}

もう一度(6)

\begin{align*}\int_{t}^{t+\Delta t}\left [\int_{CV}\frac{\partial T}{\partial t}\,dV\, \right ]\,dt=\int_{t}^{t+\Delta t}\left [ \bigg(DA\frac{\partial T}{\partial x}\bigg)_{e}-\bigg(DA\frac{\partial T}{\partial x}\bigg)_{w}\right ]\, dt\end{align*}
の離散化を$\theta$も載せてまとめると

$\theta$(6)の離散化時間積分の解法
\begin{align*}\theta =0\end{align*}
\begin{align*}\left [\big(F_{P}^{O}\big)_{e}-\big(F_{P}^{O}\big)_{w}\right ]\, \Delta t\end{align*}
陽解法
\begin{align*}\theta =1\end{align*}
\begin{align*}\left [\big(F_{P}\big)_{e}-\big(F_{P}\big)_{w}\right ]\, \Delta t\end{align*}
完全陰解法
\begin{align*}\theta =\frac{1}{2}\end{align*}
\begin{align*}\left [\bigg(\frac{F_{P}+F_{P}^{o}}{2}\bigg)_{e}-\bigg(\frac{F_{P}+F_{P}^{o}}{2}\bigg)_{w}\right ]\, \Delta t\end{align*}
陰解法
（クランクニコルソン法）
\begin{align*}\theta\end{align*}
\begin{align*}\left [\bigg(\theta F_{P}+(1-\theta)F_{P}^{o}\bigg)_{e} \\
-\bigg(\theta F_{P}+(1-\theta)F_{P}^{o}\bigg)_{w}\right ]\, \Delta t\end{align*}
  • \begin{align*}\theta =0\end{align*}
    : 陽解法
  • \begin{align*}0 < \theta \leq 1\end{align*}
    : 陰解法

$\theta$に関しては、

\begin{align*}
\left\{\begin{matrix}
\theta =0 & 陽解法 \\
0 < \theta \leq 1 &　陰解法
\end{matrix}\right.
\end{align*}

となります。
ここで、$DA\frac{\partial T}{\partial x}=F$と置いたことを思い出すと以下のようにまとまります。

$\theta$(6)の離散化時間積分の解法
$\theta =0$
\begin{align*}\left [\bigg(DA\frac{\partial T_{P}^{o}}{\partial x}\bigg)_{e}-\bigg(DA\frac{\partial T_{P}^{o}}{\partial x}\bigg)_{w}\right ]\, \Delta t\end{align*}
陽解法
$\theta =1$
\begin{align*}\left [\bigg(DA\frac{\partial T_{P}}{\partial x}\bigg)_{e}-\bigg(DA\frac{\partial T_{P}}{\partial x}\bigg)_{w}\right ]\, \Delta t\end{align*}
完全陰解法
$\theta =\frac{1}{2}$
\begin{align*}
\left [\bigg(DA\frac{\frac{\partial T_{P}}{\partial x }+\frac{\partial T_{P}^{o}}{\partial x}}{2}\bigg)_{e}-\bigg( DA\frac{\frac{\partial T_{P}}{\partial x }+\frac{\partial T_{P}^{o}}{\partial x}}{2}\bigg)_{w}\right ]\, \Delta t\end{align*}
陰解法
（クランクニコルソン法）
$\theta$
\begin{align*}\left [\left\{\theta\bigg(DA\frac{\partial T_{P}}{\partial x}\bigg) +(1-\theta) \bigg(DA\frac{\partial T_{P}^{o}}{\partial x}\bigg)\right\}_{e} \\
-\left\{\theta\bigg( DA\frac{\partial T_{P}}{\partial x}\bigg) +(1-\theta) \bigg(DA\frac{\partial T_{P}^{o}}{\partial x}\bigg)\right\}_{w}\right ]\, \Delta t\end{align*}
  • \begin{align*}\theta =0\end{align*}
    : 陽解法
  • \begin{align*}0 < \theta \leq 1\end{align*}
    : 陰解法

今までの流れから得られた結果を整理すると以下のようになります。

\begin{align*}
\frac{T_{P}-T_{P}^{o}}{\Delta t}\Delta t \Delta V &= \left [\left\{\theta\bigg(DA\frac{\partial T_{P}}{\partial x}\bigg) +(1-\theta) \bigg(DA\frac{\partial T_{P}^{o}}{\partial x}\bigg)\right\}_{e} \\
-\left\{\theta\bigg( DA\frac{\partial T_{P}}{\partial x}\bigg) +(1-\theta) \bigg(DA\frac{\partial T_{P}^{o}}{\partial x}\bigg)\right\}_{w}\right ]\, \Delta t\tag{10}
\end{align*}

空間微分の離散化と時間積分

空間微分の離散化と時間項の積分をどのように扱うかを決めなければなりません。
そこで本記事では以下として取り扱います。

  1. 空間微分の離散化：$\frac{\partial T}{\partial x}$は中心差分
  2. 時間積分：$\theta=0$の陽解法

※上記の選択をどのようにするかによって数値解の振る舞いが変わってくることを意識する必要があります。

まずは(10)の$\theta=0$をすると右辺は$\frac{T_{P}-T_{P}^{o}}{\Delta t}\Delta t \Delta V = \left [\big(DA\frac{\partial T_{P}^{o}}{\partial x}\big)_{e} -\big(DA\frac{\partial T_{P}^{o}}{\partial x}\big)_{w}\right ]\, \Delta t$と簡単になります。

空間微分に関しては格子点$P$に対して両隣の格子点を使って表す中心差分を用いると、$\big(DA\frac{\partial T}{\partial x}\big)_{e}=DA\frac{T_{E}-T_{P}}{\Delta x}$、$\big(DA\frac{\partial T}{\partial x}\big)_{w}=DA\frac{T_{P}-T_{W}}{\Delta x}$という結果を用いると(10)は、

\begin{align*}
\frac{T_{P}-T_{P}^{o}}{\Delta t}\Delta t \Delta V = \left [DA\frac{T_{E}^{o}-T_{P}^{o}}{\Delta x} -DA\frac{T_{P}^{o}-T_{W}^{o}}{\Delta x}\right ]\, \Delta t\tag{11}
\end{align*}

右辺は$t$での温度$T^{o}$のみを使っていることに着目してください。
非定常の微分方程式（温度$T$が時間変化する）において、$t$から$t+\Delta t$での$T$、つまり$T_{P}$を求めることが必要になります。(11)の左辺のみに$T_{P}$があるため$T_{P}$について式を整理することができます。

ただし、(11)は境界面の隣の格子点以外での離散化であり、境界の格子点は(11)とは別の形で式を立てる必要があります。

境界での離散化の式

例えば以下の5つの格子点（5つのCV）を考えるとします。
格子点$P$が左の界面を含む場合、(11)を修正する必要があることがわかります。

\begin{align*}
\frac{T_{P}-T_{P}^{o}}{\Delta t}\Delta t \Delta V = \left [DA\frac{T_{E}^{o}-T_{P}^{o}}{\Delta x} -DA\frac{T_{P}^{o}-T_{W}^{o}}{\Delta x}\right ]\, \Delta t\tag{11}
\end{align*}

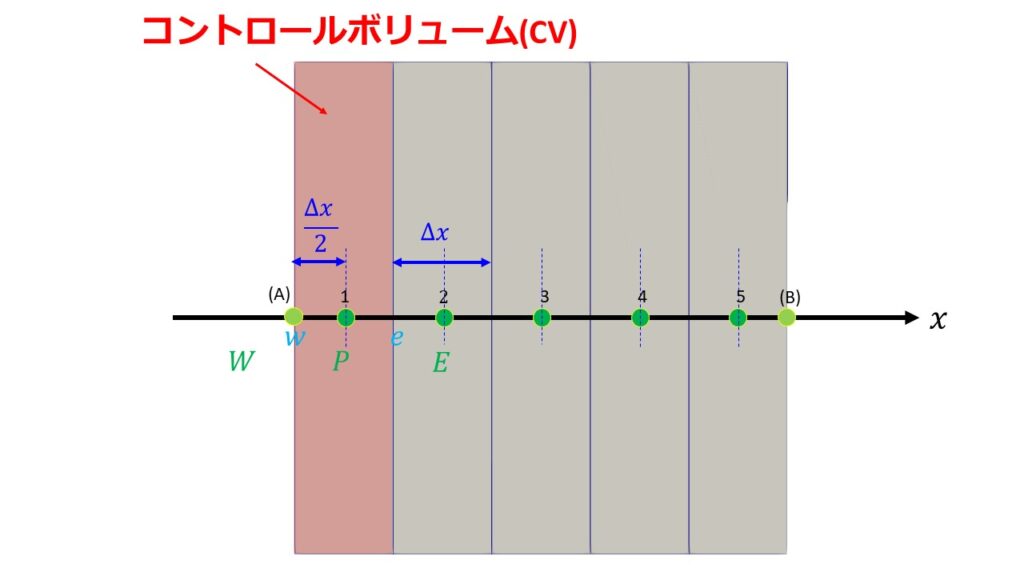
$T_{W}^{o}$が存在しないため、修正箇所は$T_{W}^{o}$を$T_{A}$に変え、$\Delta x$を$\frac{\Delta x}{2}$です。
つまり、格子点1に関して$\big(\frac{\partial T}{\partial x}\big)_{w}=\frac{T_{P}^{o}-T_{A}}{\Delta x /2}$と近似するということです。

\begin{align*}
\frac{T_{P}-T_{P}^{o}}{\Delta t}\Delta t \Delta V = \left [DA\frac{T_{E}^{o}-T_{P}^{o}}{\Delta x} -DA\frac{T_{P}^{o}-T_{A}}{\Delta x/2}\right ]\, \Delta t\tag{12}
\end{align*}

同様に、格子点$P$が右の界面を含む場合、(11)を修正する必要があることがわかります。

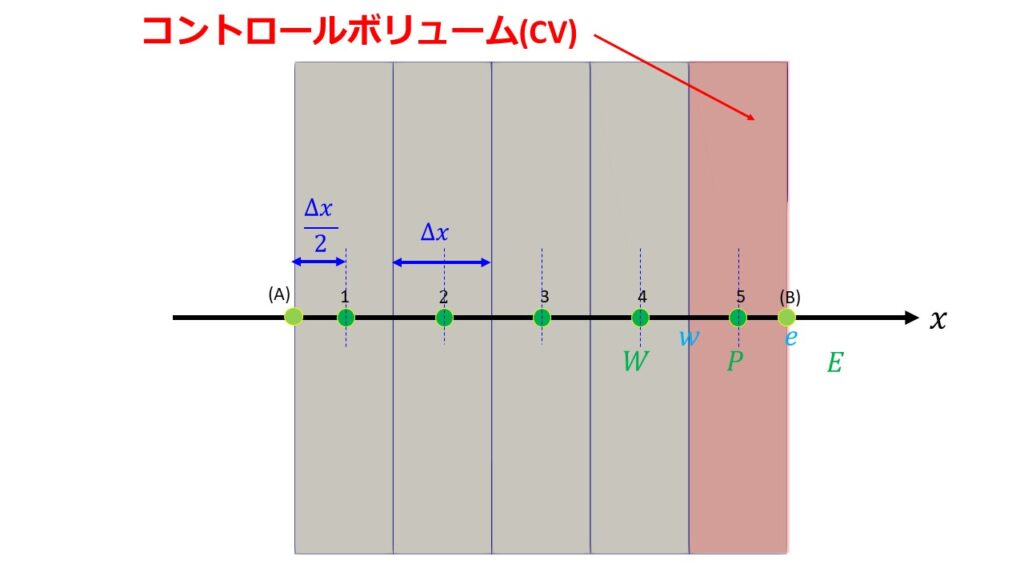
$T_{E}^{o}$が存在しないため、修正箇所は$T_{E}^{o}$を$T_{B}$に変え、$\Delta x$を$\frac{\Delta x}{2}$です。
つまり、格子点5に関して$\big(\frac{\partial T}{\partial x}\big)_{e}=\frac{T_{B}-T_{P}^{o}}{\Delta x /2}$と近似するということです。

\begin{align*}
\frac{T_{P}-T_{P}^{o}}{\Delta t}\Delta t \Delta V = \left [DA\frac{T_{B}-T_{P}^{o}}{\Delta x/2} -DA\frac{T_{P}^{o}-T_{W}^{o}}{\Delta x}\right ]\, \Delta t\tag{13}
\end{align*}

以上を界面を含むCVとそれ以外でまとめると、

格子点1
\begin{align*}
\frac{T_{P}-T_{P}^{o}}{\Delta t}\Delta t \Delta V \\
= \left [DA\frac{T_{E}^{o}-T_{P}^{o}}{\Delta x} -DA\frac{T_{P}^{o}-T_{A}}{\Delta x/2}\right ]\, \Delta t\end{align*}
格子点2~4
\begin{align*}
\frac{T_{P}-T_{P}^{o}}{\Delta t}\Delta t \Delta V\\
= \left [DA\frac{T_{E}^{o}-T_{P}^{o}}{\Delta x} -DA\frac{T_{P}^{o}-T_{W}^{o}}{\Delta x}\right ]\, \Delta t
\end{align*}
格子点5
\begin{align*}
\frac{T_{P}-T_{P}^{o}}{\Delta t}\Delta t \Delta V \\
= \left [DA\frac{T_{B}-T_{P}^{o}}{\Delta x/2} -DA\frac{T_{P}^{o}-T_{W}^{o}}{\Delta x}\right ]\, \Delta t
\end{align*}

行列にまとめる

求めるのは$t+\Delta t$における$T_{P}$の値であるため上記の表を整理します。

ここで、CVの界面の面積$A$や拡散係数$D$は定数とします。
※もちろん各CVの形が異なる場合や拡散係数が温度依存・空間依存する場合は定数ではなくなりますが、今回は定数として取り扱うことにします。
すると、$\Delta V=A\Delta x$であるため格子点2~4に関しては以下のようになります。

\begin{align*}
\frac{T_{P}-T_{P}^{o}}{\Delta t}\Delta t A\Delta x= DA\left [\bigg(\frac{T_{E}^{o}-T_{P}^{o}}{\Delta x}\bigg)_{e} -\bigg(\frac{T_{P}^{o}-T_{W}^{o}}{\Delta x}\bigg)_{w}\right ]\, \Delta t
\end{align*}

これを$T_{P}$を求める式にします。
格子点2~4

\begin{align*}
\bigg(\frac{\Delta x}{\Delta t}\bigg)T_{P}=\bigg(\frac{D}{\Delta x}\bigg)T_{W}^{o}+\bigg(\frac{D}{\Delta x}\bigg)T_{E}^{o}+\bigg(\frac{\Delta x}{\Delta t}-\frac{D}{\Delta x}-\frac{D}{\Delta x}\bigg)T_{P}^{o}\tag{14}
\end{align*}

同様に格子点1、5も$T_{P}$を求める式にします。

格子点1

\begin{align*}
\bigg(\frac{\Delta x}{\Delta t}\bigg)T_{P}=0+\bigg(\frac{D}{\Delta x}\bigg)T_{E}^{o}+\bigg(\frac{\Delta x}{\Delta t}-\frac{D}{\Delta x}\bigg)T_{P}^{o}+\frac{2D}{\Delta x}\big(-T_{P}^{o}+T_{A}\big)\tag{15}
\end{align*}

格子点5

\begin{align*}
\bigg(\frac{\Delta x}{\Delta t}\bigg)T_{P}=\bigg(\frac{D}{\Delta x}\bigg)T_{W}^{o}+0+\bigg(\frac{\Delta x}{\Delta t}-\frac{D}{\Delta x}\bigg)T_{P}^{o}+\frac{2D}{\Delta x}\big(T_{B}-T_{P}^{o}\big)\tag{16}
\end{align*}

となります。

これらを以下の形になるようにまとめます。

\begin{align*}
a_{P}T_{P}=a_{W}T_{W}^{o}+a_{E}T_{E}^{o}+\bigg(a_{P}^{o}-\big(a_{W}+a_{E}\big)\bigg)T_{P}^{o}+S_{u}\tag{17}
\end{align*}

以上をまとめると

\begin{align*}a_{P}=a_{P}^{o}\end{align*}
\begin{align*}a_{W}\end{align*}
\begin{align*}a_{E}\end{align*}
\begin{align*}a_{P}^{o}-\big(a_{W}+a_{W}\big)\end{align*}
\begin{align*}S_{u}\end{align*}
格子点1
\begin{align*}\frac{\Delta x}{\Delta t}\end{align*}
\begin{align*}\frac{D}{\Delta x}\end{align*}
0
\begin{align*}\frac{\Delta x}{\Delta t}-\frac{D}{\Delta x}\end{align*}
\begin{align*}\frac{2D}{\Delta x}\big(-T_{P}^{o}+T_{A}\big)\end{align*}
格子点2~4
\begin{align*}\frac{\Delta x}{\Delta t}\end{align*}
\begin{align*}\frac{D}{\Delta x}\end{align*}
\begin{align*}\frac{D}{\Delta x}\end{align*}
\begin{align*}\frac{\Delta x}{\Delta t}-\frac{D}{\Delta x}-\frac{D}{\Delta x}\end{align*}
0
格子点5
\begin{align*}\frac{\Delta x}{\Delta t}\end{align*}
0
\begin{align*}\frac{D}{\Delta x}\end{align*}
\begin{align*}\frac{\Delta x}{\Delta t}-\frac{D}{\Delta x}\end{align*}
\begin{align*}\frac{2D}{\Delta x}\big(T_{B}-T_{P}^{o}\big)\end{align*}

このようになります。

各係数はCVの形状や物性値によって決まっている値であるため定数です。
以上の表をもとに、行列計算を行い$T_{P}$の時間変化を求めることができます。

まとめ

今回は有限体積法の基礎的な理解のために1次元熱拡散方程式を有限体積法で求めるまでの流れを解説しました。

1次元熱拡散方程式

\begin{align*}
\frac{\partial T}{\partial t} = \frac{\partial}{\partial x}\bigg(D\frac{\partial T}{\partial x}\bigg)\tag{2}
\end{align*}

(2)を有限体積法で求めた離散化式は、界面を含むCVとそれ以外でまとめると、

格子点1
\begin{align*}
\frac{T_{P}-T_{P}^{o}}{\Delta t}\Delta t \Delta V \\
= \left [DA\frac{T_{E}^{o}-T_{P}^{o}}{\Delta x} -DA\frac{T_{P}^{o}-T_{A}}{\Delta x/2}\right ]\, \Delta t\end{align*}
格子点2~4
\begin{align*}
\frac{T_{P}-T_{P}^{o}}{\Delta t}\Delta t \Delta V\\
= \left [DA\frac{T_{E}^{o}-T_{P}^{o}}{\Delta x} -DA\frac{T_{P}^{o}-T_{W}^{o}}{\Delta x}\right ]\, \Delta t
\end{align*}
格子点5
\begin{align*}
\frac{T_{P}-T_{P}^{o}}{\Delta t}\Delta t \Delta V \\
= \left [DA\frac{T_{B}-T_{P}^{o}}{\Delta x/2} -DA\frac{T_{P}^{o}-T_{W}^{o}}{\Delta x}\right ]\, \Delta t
\end{align*}

となります。
ただし、以下のもとで行った離散化の式であることに注意する必要があります。

  1. 空間微分の離散化：$\frac{\partial T}{\partial x}$は中心差分
  2. 時間積分：$\theta=0$の陽解法

空間微分を中心差分とは異なる方法、時間積分は陰解法などで行った場合は上記の離散化式も形を変えますし、解の振る舞いも変わります。
連続な場に対しての偏微分方程式をどのように離散化して近似するかも重要だということです。

次回の記事では本記事で導いた1次元熱拡散方程式の有限体積法の離散化を具体的な境界条件で得られる計算について解説を行います。

次回の記事

【具体的な計算】1次元熱拡散方程式（熱伝導方程式）の有限体積法を解説(2)

参考書

有限体積法の勉強にはこの本で間違いないです。

数値流体力学 ［第2版］

数値流体力学 ［第2版］

H.K.Versteeg, W.Malalasekera
10,450円(04/19 21:24時点)

Amazon楽天市場Yahoo

Amazonの情報を掲載しています
関連記事もどうぞ

COMMENT

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です