こんにちは（@t_kun_kamakiri）
本記事では流体解析の離散化である有限体積法について基礎的な解説を行います。
有限体積法はOpenFOAMなど流体解析でも使われる離散化の方法です。流体解析用ソフトの多くが有限体積法を採用しており、人によってはプログラムを実装したことがないがために有限体積法のイメージが付かないという方も多いかと思います。
有限体積法のわかりやすい解説記事もなかなかないため、自身で勉強したことをわかりやすく解説する記事を残しておこうと思っています。
- 数値流体の有限体積法の基礎を学びたい方
- OpenFOAMで使われる有限体積法を学びたい方
前回の記事では1次元熱拡散方程式の有限体積法の離散化を行いました。
以下で簡単におさらいをしておきましょう。
1次元熱拡散方程式
\frac{\partial T}{\partial t} = \frac{\partial}{\partial x}\bigg(D\frac{\partial T}{\partial x}\bigg)\tag{1}
\end{align*}
有限体積法で求めた離散化式は、界面を含むCVとそれ以外でまとめると、
| 格子点1 | \begin{align*} \frac{T_{P}-T_{P}^{o}}{\Delta t}\Delta t \Delta V \\ = \left [DA\frac{T_{E}^{o}-T_{P}^{o}}{\Delta x} -DA\frac{T_{P}^{o}-T_{A}}{\Delta x/2}\right ]\, \Delta t\end{align*} |
| 格子点2~4 | \begin{align*} \frac{T_{P}-T_{P}^{o}}{\Delta t}\Delta t \Delta V\\ = \left [DA\frac{T_{E}^{o}-T_{P}^{o}}{\Delta x} -DA\frac{T_{P}^{o}-T_{W}^{o}}{\Delta x}\right ]\, \Delta t \end{align*} |
| 格子点5 | \begin{align*} \frac{T_{P}-T_{P}^{o}}{\Delta t}\Delta t \Delta V \\ = \left [DA\frac{T_{B}-T_{P}^{o}}{\Delta x/2} -DA\frac{T_{P}^{o}-T_{W}^{o}}{\Delta x}\right ]\, \Delta t \end{align*} |
となります。
ただし、以下のもとで行った離散化の式であることに注意する必要があります。
- 空間微分の離散化：$\frac{\partial T}{\partial x}$は中心差分
- 時間積分：$\theta=0$の陽解法
空間微分を中心差分とは異なる方法、時間積分は陰解法などで行った場合は上記の離散化式も形を変えますし、解の振る舞いも変わります。
連続な場に対しての偏微分方程式をどのように離散化して近似するかも重要だということです。
前回の記事では、以上のような結果を導きました。
今回はこちらの式を使ってより具体的な境界条件と物理量の設定を行い計算を行います。
有限体積法の基礎を体験するため、できるだけ手を動かしながら体験できるような内容にしています。
- 熱拡散方程式を有限体積法で離散化
- 有限体積法を手計算で導出する
本記事が有限体積法の第一歩として参考になれば幸いです。
条件設定
まずは解きたい問題を設定します。
長さ$L=2$cm$=2\times 10^{-2}$mで両端の境界条件は、左端は断熱条件とし、右端は温度規定$20^\circ C$とします。
断熱条件は、フーリエの法則より熱流束$\dot{q}=-k\frac{\partial T}{\partial x}$が0なので温度勾配$\frac{\partial T}{\partial x}$が0を意味します。
\left\{\begin{matrix}
x=0 & \frac{\partial T}{\partial x}=0\\
x=L & T_{B} =20^\circ C
\end{matrix}\right.
\end{align*}
解くべき方程式は1次元の熱拡散方程式（熱伝導方程式）で以下の式に従います。
1次元熱拡散方程式
\frac{\partial T}{\partial t} = \frac{\partial}{\partial x}\bigg(D\frac{\partial T}{\partial x}\bigg)\tag{1}
\end{align*}
物性値として、熱拡散係数$D=\frac{k}{\rho c}=10^{-6}$とします。
※$c[J/K\cdot kg]$は熱容量、$\rho[kg/m^{3}]$は密度。$\rho c = 10\times 10^{-6}[J/m^{3}\cdot K]$
※熱伝導率：$k=10[W/m\cdot k]$
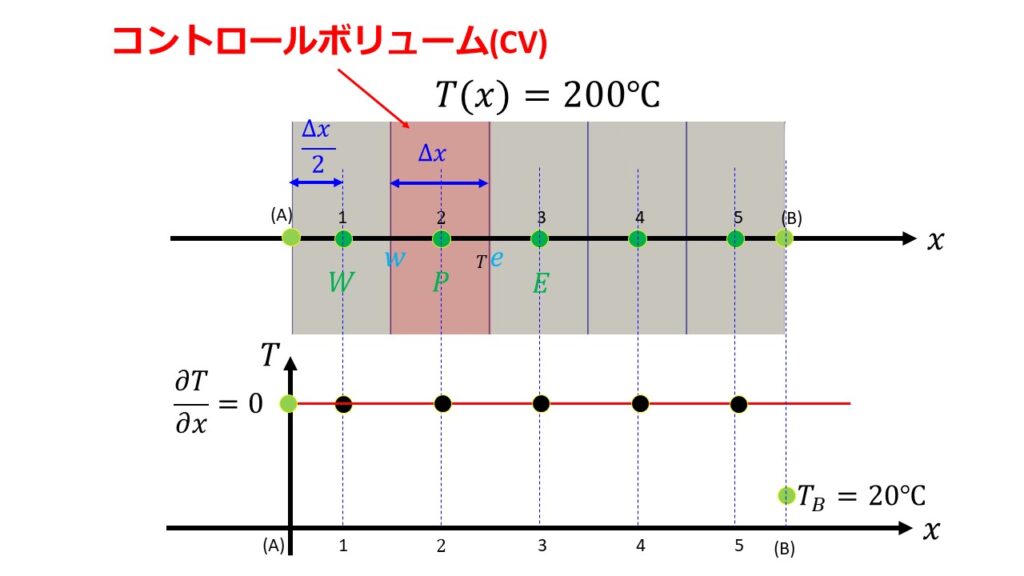
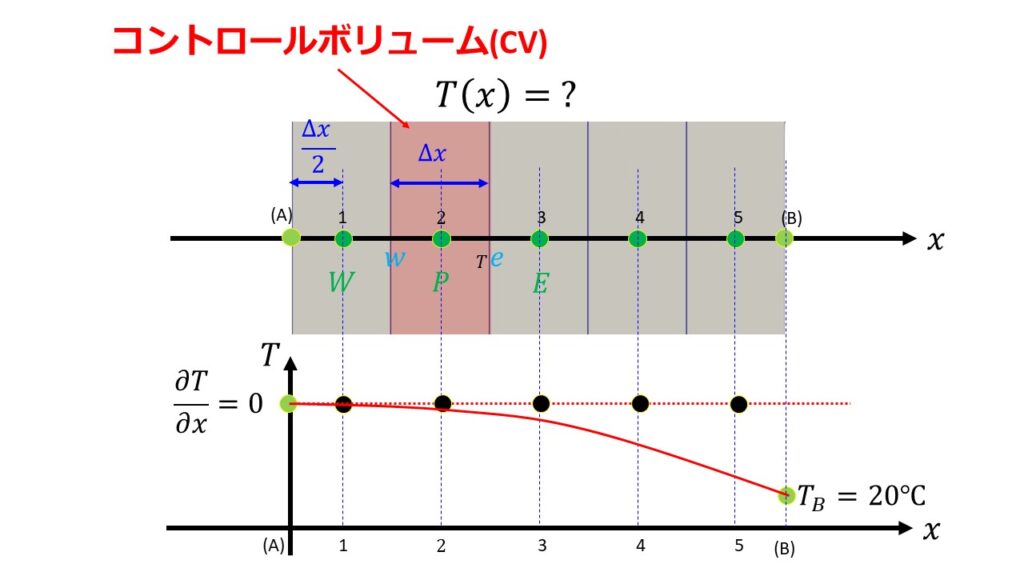
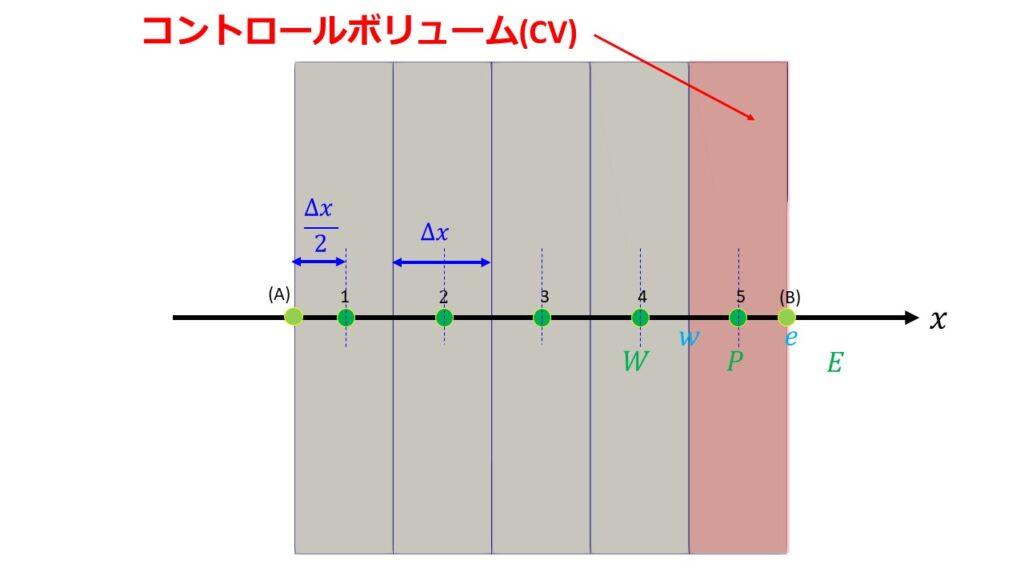
コントロールボリューム(以下CVと略す）は５つあり、格子点は1～5の5つの場合を考えます。
はじめに全体が温度$T=200^\circ C$と均一に保たれているとします。
そして、初期条件$t=0$で右端の温度を$T_{B}=20^\circ C$としたとき全体の温度分布が時間によってどのように変化するのか求めます。
- 分割幅$\Delta x=0.004[m]$
- 時間刻み$\Delta t=2$
本記事では手計算での結果を解説しますが、厳密解との比較も行います。
また、次回の記事ではOpenFOAMを使ったシミュレーションの結果との比較も行います。
解析設定をどのようにするのかによって結果が変わってくるのを体験することができるでしょう。
離散化
では、具体的な境界条件と物性値を有限体積法で離散化して得られた式に代入していきましょう。
ただし、以下の条件で離散化したということは意識する必要があります。
解析条件
- 空間微分の離散化：$\frac{\partial T}{\partial x}$は中心差分
- 時間積分：$\theta=0$の陽解法
境界条件に関しては、
- 格子点1の$\big(\frac{\partial T}{\partial x}\big)_{w}=\frac{T_{P}^{o}-T_{A}}{\Delta x/2}=0$
- 格子点5の$\big(\frac{\partial T}{\partial x}\big)_{e}=\frac{T_{B}-T_{P}^{o}}{\Delta x/2}$
※$T_{B}=20^\circ C$
有限体積法で求めた離散化式は、界面を含むCVとそれ以外でまとめると、
| 格子点1 | \begin{align*} \frac{T_{P}-T_{P}^{o}}{\Delta t}\Delta t \Delta V \\ = \left [DA\frac{T_{E}^{o}-T_{P}^{o}}{\Delta x} -0\right ]\, \Delta t\end{align*} |
| 格子点2~4 | \begin{align*} \frac{T_{P}-T_{P}^{o}}{\Delta t}\Delta t \Delta V\\ = \left [DA\frac{T_{E}^{o}-T_{P}^{o}}{\Delta x} -DA\frac{T_{P}^{o}-T_{W}^{o}}{\Delta x}\right ]\, \Delta t \end{align*} |
| 格子点5 | \begin{align*} \frac{T_{P}-T_{P}^{o}}{\Delta t}\Delta t \Delta V \\ = \left [DA\frac{T_{B}-T_{P}^{o}}{\Delta x/2} -DA\frac{T_{P}^{o}-T_{W}^{o}}{\Delta x}\right ]\, \Delta t \end{align*} |
これらを以下の形になるようにまとめます。
a_{P}T_{P}=a_{W}T_{W}^{o}+a_{E}T_{E}^{o}+\bigg(a_{P}^{o}-\big(a_{W}+a_{E}\big)\bigg)T_{P}^{o}+S_{u}\tag{2}
\end{align*}
以上をまとめると
\begin{align*}a_{P}=a_{P}^{o}\end{align*} |
\begin{align*}a_{W}\end{align*} |
\begin{align*}a_{E}\end{align*} |
\begin{align*}a_{P}^{o}-\big(a_{W}+a_{W}\big)\end{align*} |
\begin{align*}S_{u}\end{align*} |
|
| 格子点1 | \begin{align*}\frac{\Delta x}{\Delta t}\end{align*} |
\begin{align*}\frac{D}{\Delta x}\end{align*} |
0 | \begin{align*}\frac{\Delta x}{\Delta t}-\frac{D}{\Delta x}\end{align*} |
0 |
| 格子点2~4 | \begin{align*}\frac{\Delta x}{\Delta t}\end{align*} |
\begin{align*}\frac{D}{\Delta x}\end{align*} |
\begin{align*}\frac{D}{\Delta x}\end{align*} |
\begin{align*}\frac{\Delta x}{\Delta t}-\frac{D}{\Delta x}-\frac{D}{\Delta x}\end{align*} |
0 |
| 格子点5 | \begin{align*}\frac{\Delta x}{\Delta t}\end{align*} |
0 | \begin{align*}\frac{D}{\Delta x}\end{align*} |
\begin{align*}\frac{\Delta x}{\Delta t}-\frac{D}{\Delta x}\end{align*} |
\begin{align*}\frac{2D}{\Delta x}\big(T_{B}-T_{P}^{o}\big)\end{align*} |
このようになります。
さて、具体的な数値を代入して表にまとめましょう。
- $\frac{D}{\Delta x}=\frac{10^{-6}}{4\times 10^{-3}}$
- $\frac{\Delta x}{\Delta t}=\frac{4\times 10^{-3}}{2}$
※全体を$10^{5}$を掛けてまとめます。
\begin{align*}a_{P}=a_{P}^{o}\end{align*} |
\begin{align*}a_{W}\end{align*} |
\begin{align*}a_{E}\end{align*} |
\begin{align*}a_{P}^{o}-\big(a_{W}+a_{W}\big)\end{align*} |
\begin{align*}S_{u}\end{align*} |
|
| 格子点1 | 200 | 25 | 0 | 175 | 0 |
| 格子点2~4 | 200 | 25 | 25 | 150 | 0 |
| 格子点5 | 200 | 0 | 25 | 175 | \begin{align*}50\big(T_{B}-T_{P}^{o}\big)\end{align*} |
格子点5について、$S_{u}$の$T_{P}^{o}$があるので$a_{P}^{o}-\big(a_{W}+a_{W}\big)$の中にまとめることに注意すると、各格子点$T_{P}$については以下のようになります。
200T_{1}^{n+1}&=&0+25T_{2}^{n}+175T_{1}^{n}\\
200T_{2}^{n+1}&=&25T_{1}^{n}+25T_{3}^{n}+150T_{2}^{n} \\
200T_{3}^{n+1}&=&25T_{2}^{n}+25T_{4}^{n}+150T_{3}^{n} \\
200T_{4}^{n+1}&=&25T_{3}^{n}+25T_{5}^{n}+150T_{4}^{n} \\
200T_{5}^{n+1}&=&25T_{4}^{n}+0+125T_{5}^{n}-50\underset{20^\circ C}{T_{B}^{n}}
\end{matrix}\right.\tag{3}\end{align*}
$t+\Delta t$は$n+1$ステップ、$t$は$n$ステップに対応し上付き文字で表記しています。
(3)から$t+\Delta t$の温度$T_{P}$の値を求めるのに$t$での両隣の温度が必要であることがわかります。つまり、$n+1$ステップに対して$n$ステップでの温度が決まれば、時間に対しては温度$T_{P}$のまわりの温度で決まっていくということになります。
具体的な値を代入して結果を求める
以上の式をExcelに入力してグラフにしてみましょう。
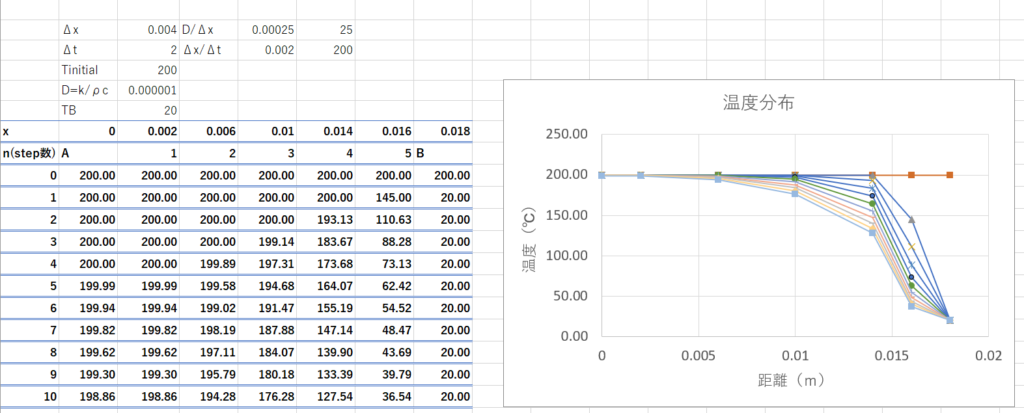
初期状態で全域で$T=200^\circ C$だったのが境界条件によって徐々に温度が拡散していっているのがわかります。
ただし、今回のような陽解法は空間刻み$\Delta x$と時間刻み$\Delta t$と物性値により不安定になることが知られています。結果だけを示すと以下の条件の安定条件がありうす。
\Delta t < \frac{(\Delta x)^2}{2D}=\frac{(0.004)^2}{2\times 10^{-6}}=8\tag{4}
\end{matrix}\right.\end{align*}
例えば以下のように$\Delta t = 8$と時間刻みを大きくすると以下のように解が振動します。
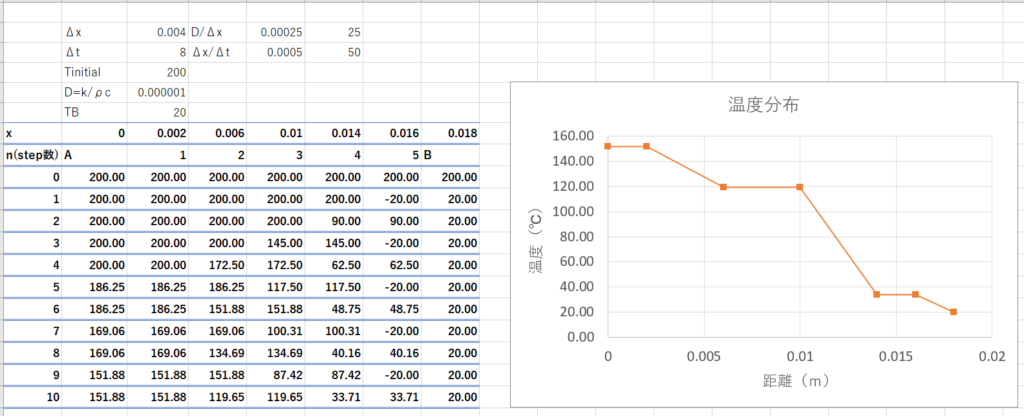つまり、解の安定性を考慮するならば$\Delta t <8$という条件が必要であるということです。
$T_{B}=0$ときの厳密解と比較
$T_{B}=0$の場合は厳密解を求めることができます。
$T_{B}=0$の場合はすぐにはわかりませんでしたので、どなたかわかる方いたらコメントください_(._.)_
厳密解は、
T(x,t)=T_{0}\frac{4}{\pi}\sum_{m=1}^{\infty}\frac{(-1)^{m+1}}{2m-1}\exp(-D\lambda_{m}^2t)\cos(\lambda_{m}x)\tag{5}
\end{align*}
※$\lambda_{m}=\frac{2m-1}{2L}$
まとめ
有限体積法で1次元熱拡散方程式を解きました。
解析設定や境界上によって結果が変わってくるということを意識しておく必要があります。
本記事で扱った条件は以下です。
解析条件
- 空間微分の離散化：$\frac{\partial T}{\partial x}$は中心差分
- 時間積分：$\theta=0$の陽解法
境界条件に関しては、
- 格子点1の$\big(\frac{\partial T}{\partial x}\big)_{w}=\frac{T_{P}^{o}-T_{A}}{\Delta x/2}=0$
- 格子点5の$\big(\frac{\partial T}{\partial x}\big)_{e}=\frac{T_{B}-T_{P}^{o}}{\Delta x/2}$
※$T_{B}=20^\circ C$
境界条件は物理的に現象が変わる重要な条件ですが、空間刻みや時間刻みによる解析条件によって解の振る舞いが変わってしまうというのは思わしくありません。
微分を離散化した際に近似して落とした項が、どのように精度や解の安定性に影響を及ぼすというのは十分に意識する必要があります。
参考書
有限体積法の勉強にはこの本で間違いないです。
Follow @t_kun_kamakiri
