こんにちは(@t_kun_kamakiri)
過去に書いたグロス・ピタエフスキー(GP)方程式のFortranコードを保存用として記載しておきます。GP方程式については下記の記事に詳しく書きましたのでご参考ください。
グロス・ピタエフスキー方程式(略してGP方程式)
i\hbar\frac{\partial \psi(\boldsymbol{r},t)}{\partial t}=-\frac{\hbar^2}{2m}\nabla^2\psi(\boldsymbol{r},t)+V_{ex}\psi(\boldsymbol{r},t)+g|\psi(\boldsymbol{r},t)|^2\psi(\boldsymbol{r},t)\tag{1}
\end{align*}
ただし、グロス・ピタエフスキー方程式は以下の状況を仮定していることに注意。
- ボース・アインシュタイ凝縮を起こしているので、大多数の粒子の状態をまとめて1つの波動関数\(\psi\)と書く。
- ボース・アインシュタイ凝縮を起こした大多数の粒子を捕獲ポテンシャルで捕獲する。
捕獲ポテンシャル:(\(V_{ext}=\frac{m\omega^2\boldsymbol{r}^2}{2}\)) - 粒子間の相互作用は近接でのみ作用する(\(U_{int}=g\delta(\boldsymbol{r_{1}}-\boldsymbol{r_{2}})\))
※近接のみ作用するというのは希薄な気体であるという意味です。
2次元ダークソリトンの渦への崩壊
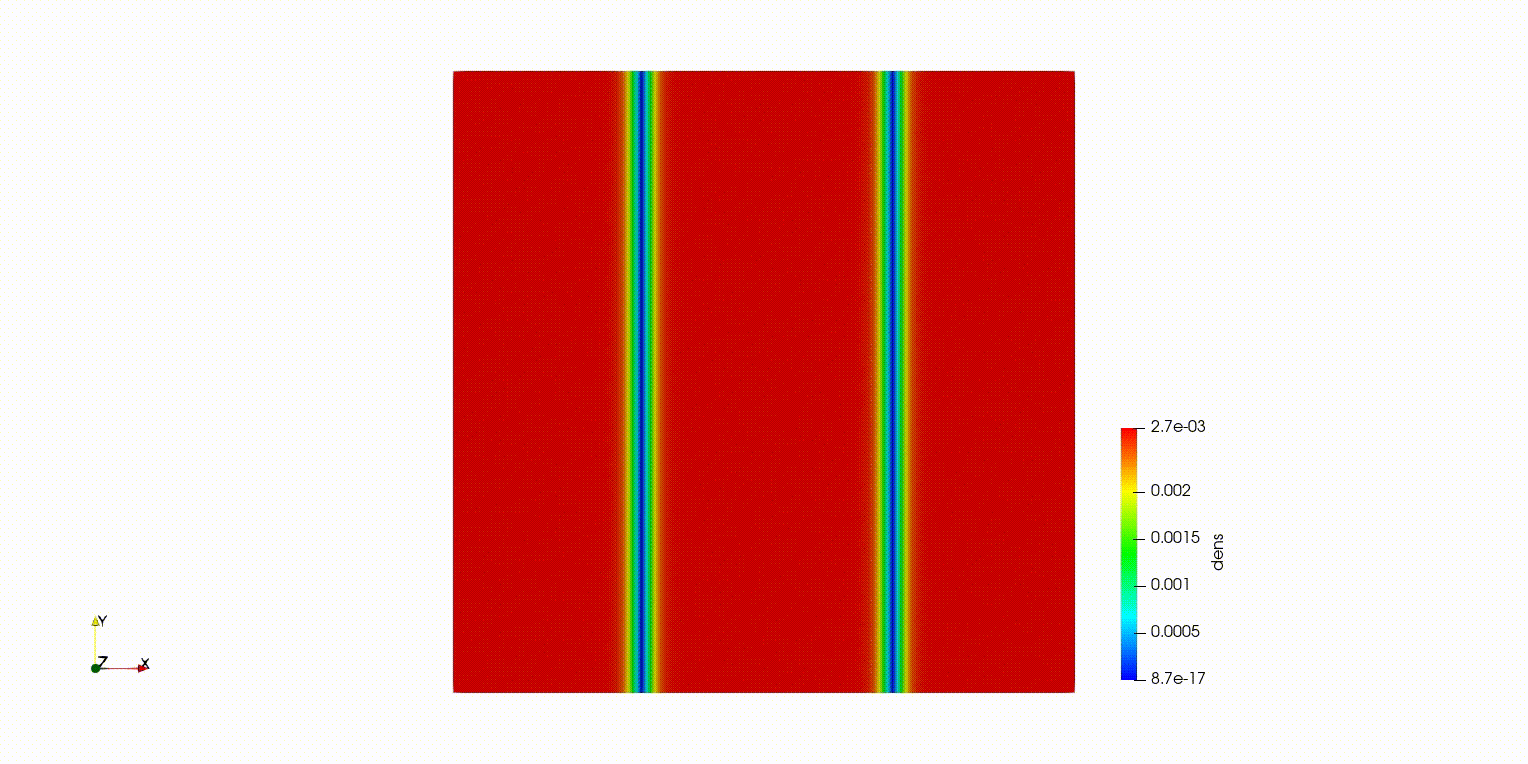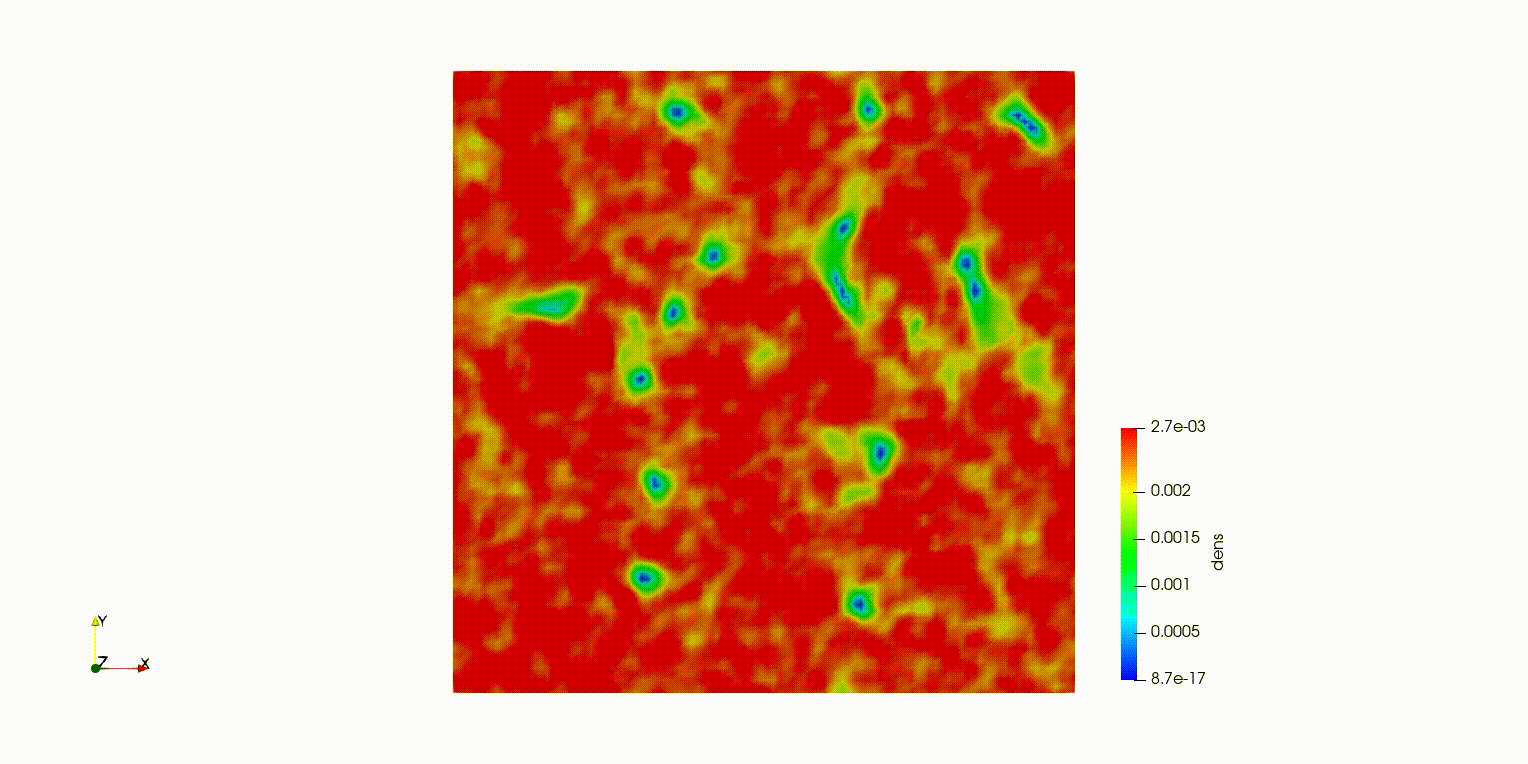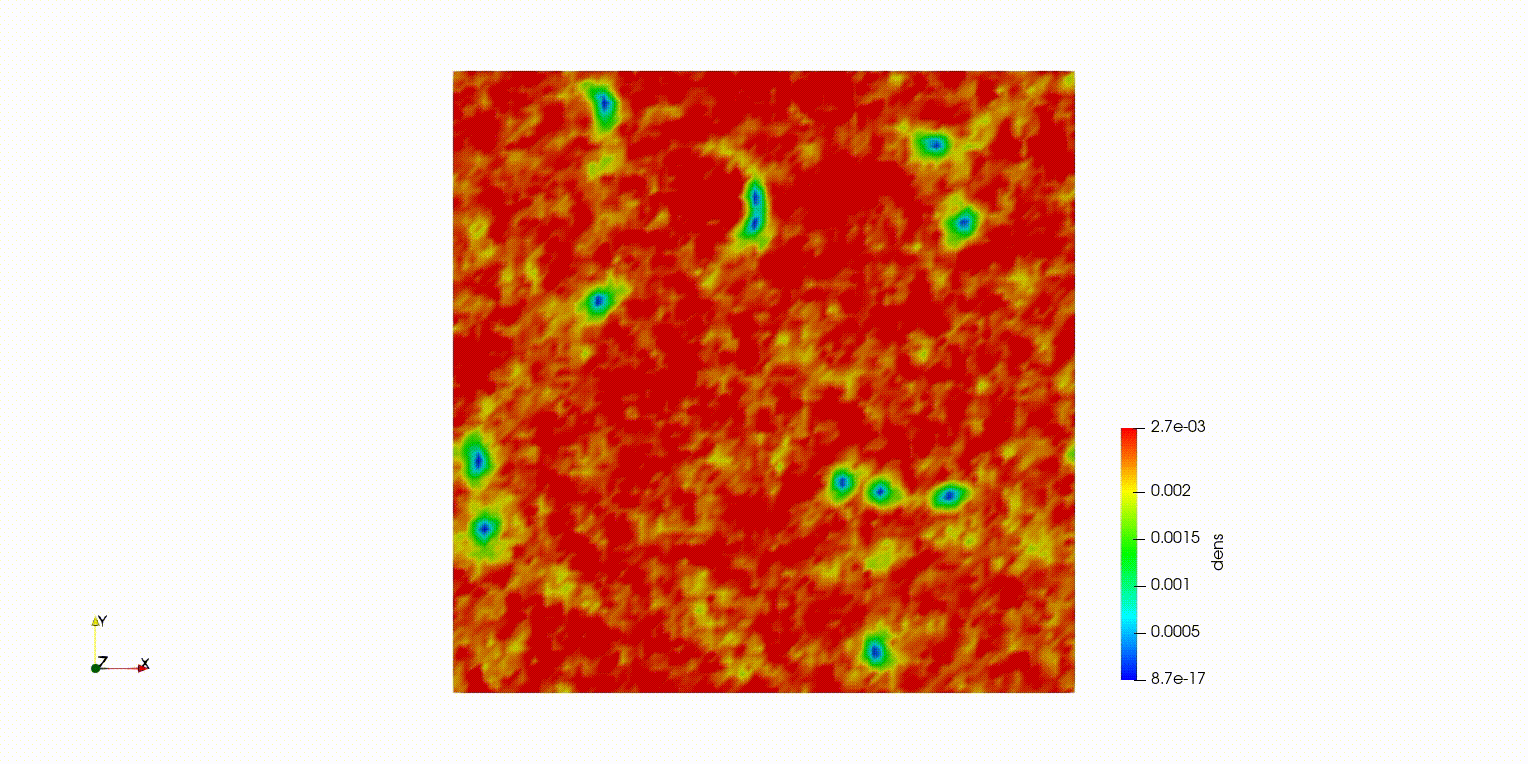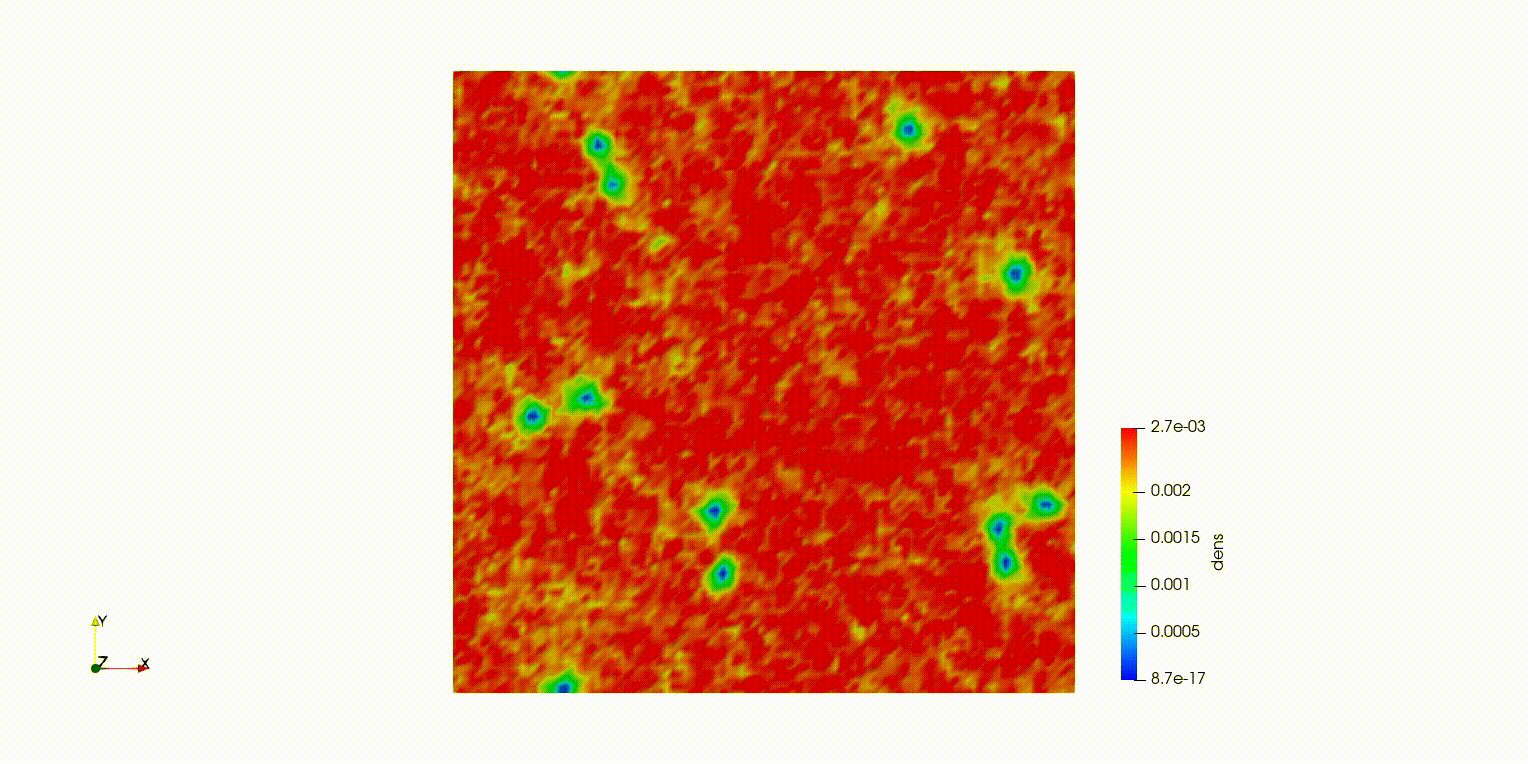
本記事で紹介するのは2次元で溝のような形をした波動関数を初期状態にして、時間発展で渦へと崩壊するというシミュレーションです。
ソリトンが崩壊して渦ができた( ^ω^)・・・
でも端の境界条件おかしい・・・Fortranで計算して、paraviewで可視化。
↓参考論文はこれ。https://t.co/ogSfPfSjoI pic.twitter.com/35BTlU6guS
— カマキリ🐲技術士勉強中 (@t_kun_kamakiri) April 15, 2019
Fortranコード
昔書いたとてもお粗末なコードがあったので後で修正するのを見越して添付しています。ところどころ古いFortranの記述もあるので見てられないですが、べた書きで凝ったことをしていません。
今改めて見ると同じ記述が何個もあったり、意味の塊でコードをまとめていなかったり、めちゃくちゃ醜いですね💦書き直したくなります・・・
参考書
Fortranの日本語書籍は数が多くないので以下自分が持っていて参考にしているものを紹介します。
以下2冊はFortran90/95で書かれたとてもわかりやすい参考書です。
基本的な文法は↓こちらで学んでおけば良いでしょう。
Fortranを使う場面はやはり数値計算でしょう。以下の参考書は微分方程式を数値的に解く際のサンプルコードが多く紹介されています。難しい記法を使わずに書いているので、わかりやすいです。
モダンなFortranに対応した参考書としては以下のものがあります。
あまり深く読めていません_(._.)_