こんにちは(@t_kun_kamakiri)
本記事では、気液混相流においてクーラン数による結果に違いが出るのかを検証します。
流体解析ツールOpenFOAMのinterFoamソルバを使います。
クーラン数による結果の違いを確認する。
OpenFOAM v2312(WSL2)
解析対象
解析の対象はこちらです。

右(実験)、左(数値計算)
こちらをOpenFOAMを使って再現します。
モデルの作り方は下記の記事に詳しく書いていますので、ご参考ください。
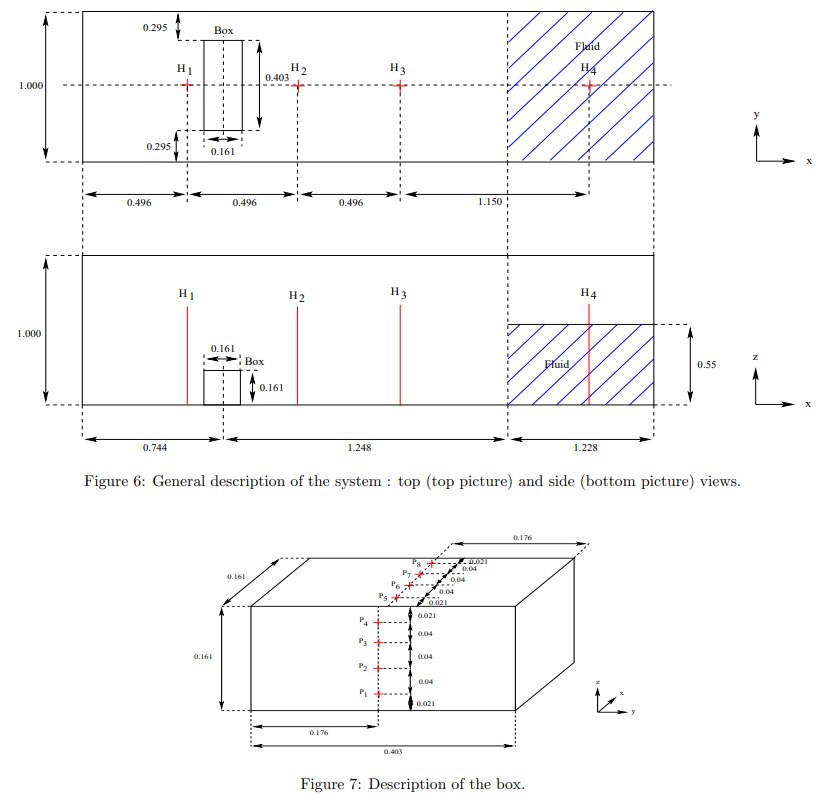

実験では初期状態で青斜線で囲まれた領域に水をセットし、時刻0秒で開放します。
その後水はBoxと書かれた障害物に当たり、水しぶきをあげます。
この時に実験データとして、
- p1~P8の座標で圧力の時刻歴
- H1~H4の座標での水面の高さの時刻歴
という時刻歴データを測定しています。
クーラン数について
interFoamソルバのクーラン数は、以下の2つの設定があります。
- maxAlphaCo
- maxCo
違いがよくわからなかったので、調べます。
- maxAlphaCo(相の場についてのクーラン数)
- maxCo(その他の場についてのクーラン数)
があり、どちらも0.5を超えないようにすることが推奨されているような記述があります。
しかし、クーラン数の大きさはそのまま時間刻みの大きさを決めるため、時間刻みが小さすぎる場合はメッシュを大きくするなど対応しないといけません。
差分法におけるクーラン数$C=\frac{u\Delta t}{\Delta x}$を考えるとイメージしやすいと思います。
$\Delta t$が小さくなりすぎる場合、
- 精度を無視してクーラン数$C$を大きくする
- メッシュサイズ$\Delta x$を大きくする
などが考えられます。
方程式の解き方として陽解法で解く場合は、クーラン数を1以下にしなければ、計算自体が不安定で発散を招きます。
一方、陰解法であればクーラン数による縛りはなく安定(発散しないわけではない)なので、クーラン数を大きくとるのもひとつの手です。
$\Delta t$を1より大きくとるのため、精度が悪くなります。また、発散する可能性も含んでいるので注意が必要です。
クーラン数違いによるスタディ
system/controlDict
|
1 2 3 4 5 |
adjustTimeStep yes; maxCo 0.5; maxAlphaCo 0.5; |





実験(右の動画)と比較するとOpenFOAMによるシミュレーションは全然水しぶきが立っていません。
interFoamはVOF法なので、メッシュによる解像度がかなり効いてくるので、これ以上水志簿記の挙動を合わせるのは厳しそうです。
水しぶきの挙動は全然違いますが、圧力と水位はどうでしょう。
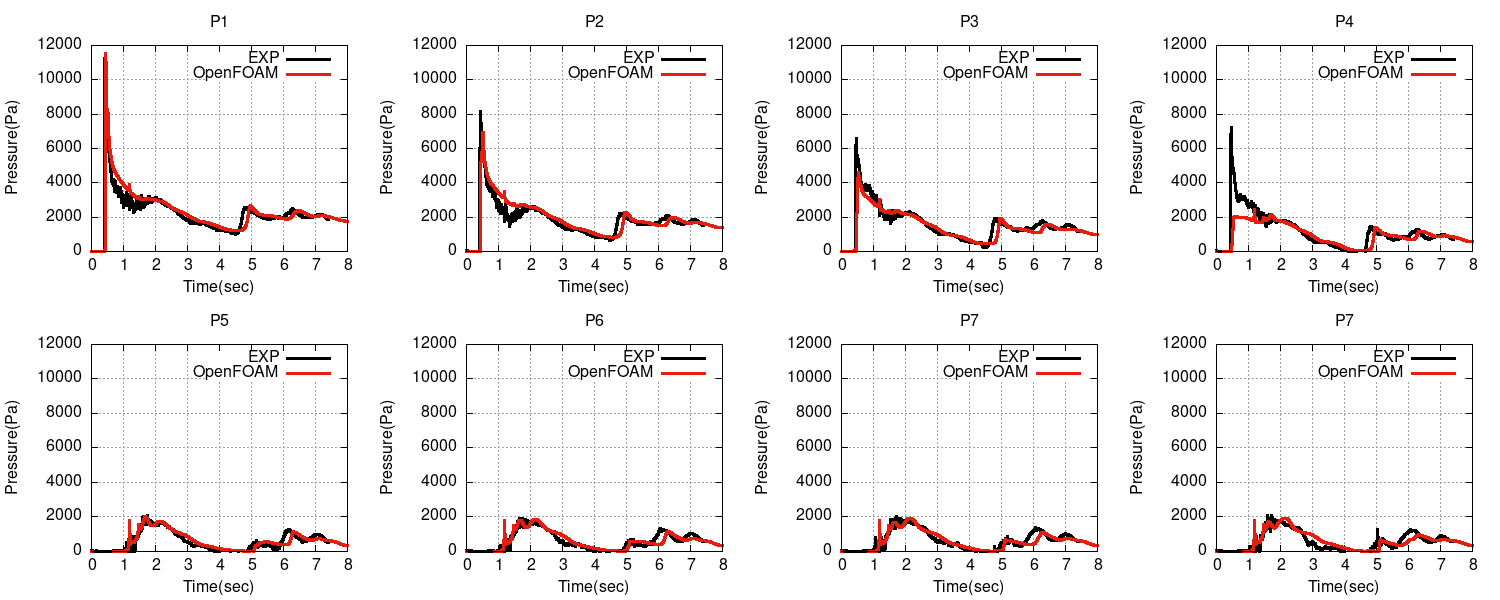
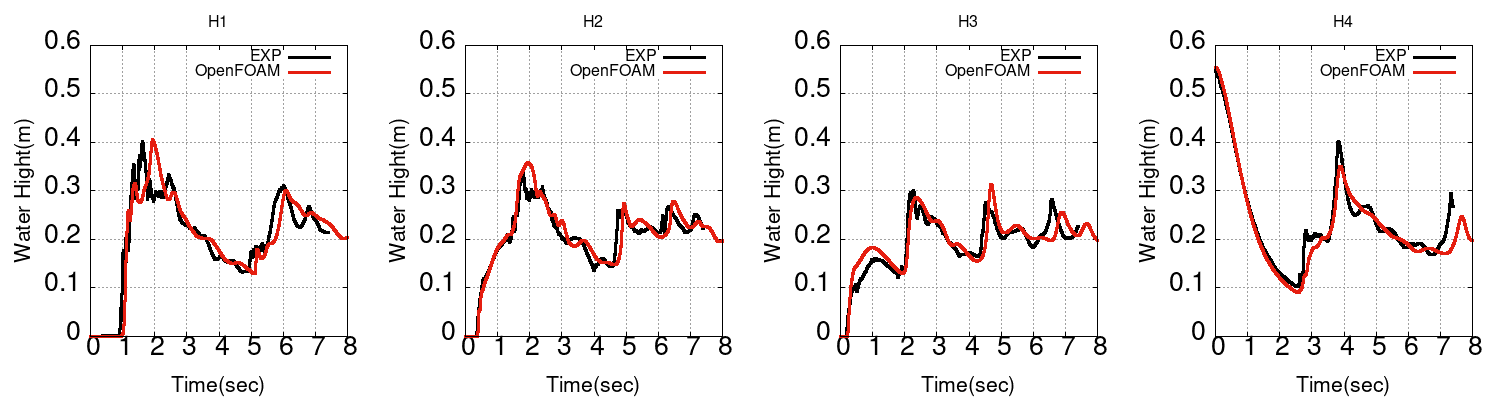
case000(maxCo 0.5、maxAlphaCo 0.5)
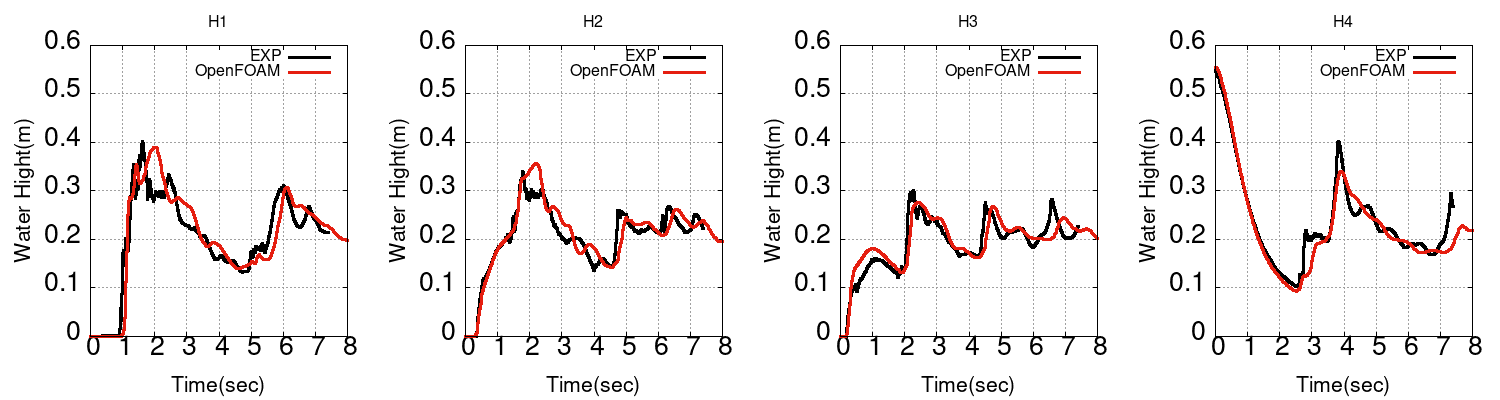
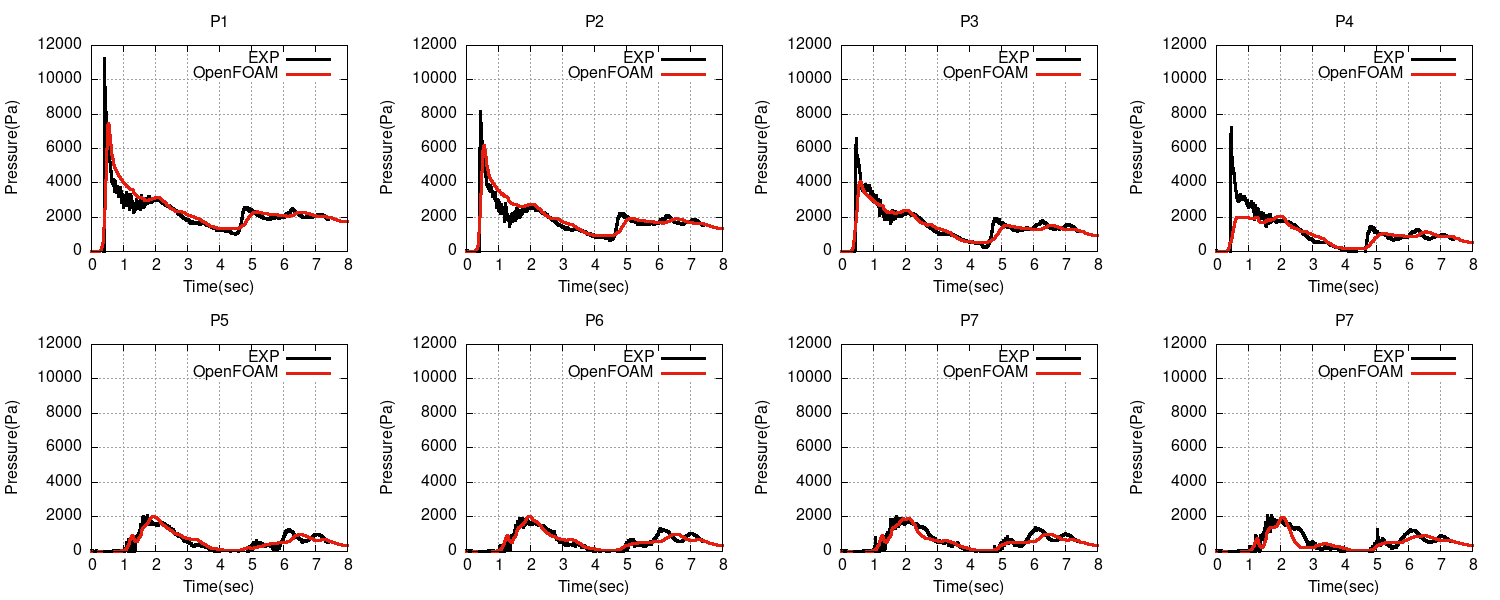
圧力と水位の時刻歴
圧力と水位はそこそこ合っていそうです。
上記「case000(maxCo 0.5、maxAlphaCo 0.5)」をベースにクーラン数を以下のように変えてみます。
| case001(左上) | maxCo 5.0; maxAlphaCo 0.5; |
| case002(右上) | maxCo 10.0; maxAlphaCo 0.5; |
| case003(左下) | maxCo 5.0; maxAlphaCo 5.0; |
| case004(右下) | maxCo 10.0; maxAlphaCo 10.0; |
こちらが結果。

水しぶきは相変わらず実験と違います。
圧力と水位をそれぞれ見てみます。
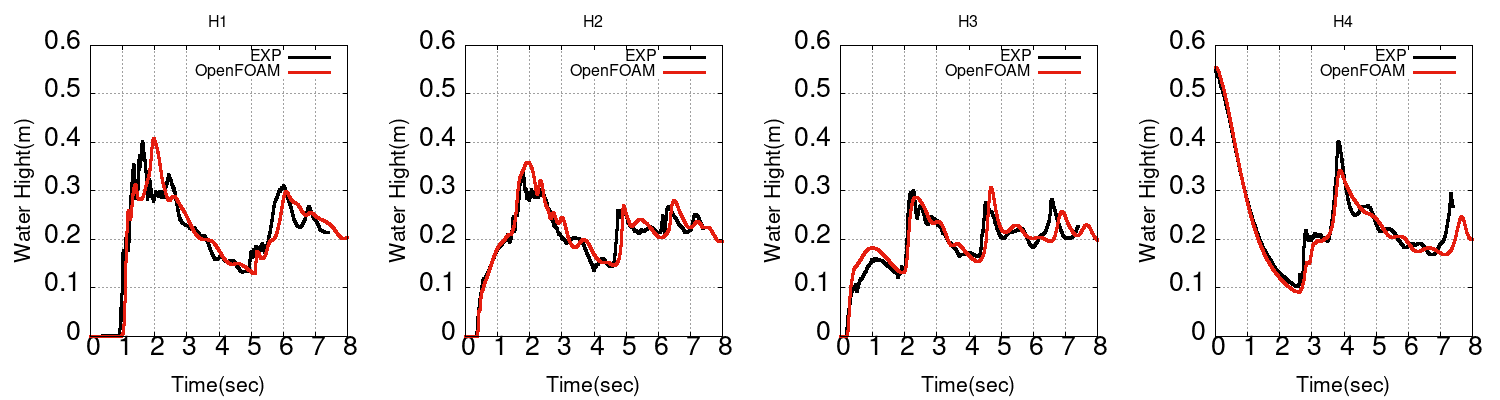
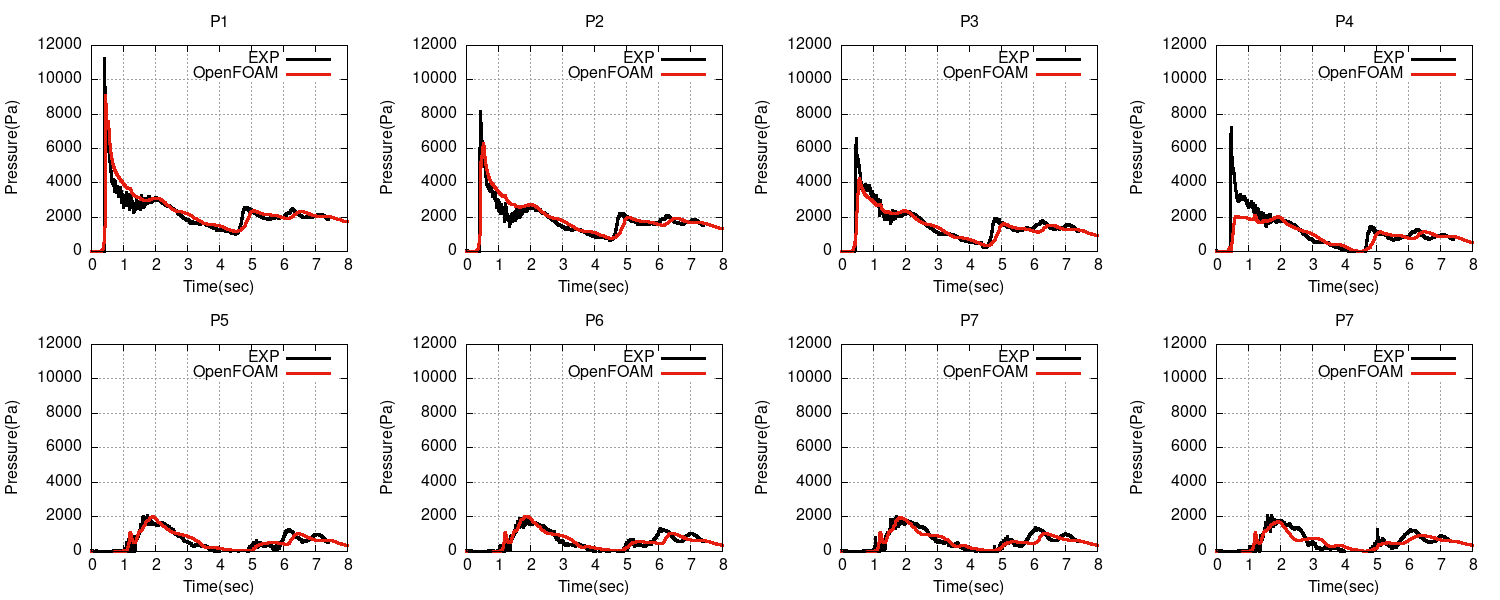
case001(maxCo 5.0、maxAlphaCo 0.5)
圧力と水位の時刻歴




それほど違いが見られません。
case002(maxCo 10.0、maxAlphaCo 0.5)
圧力と水位の時刻歴
case003(maxCo 5.0、maxAlphaCo 5.0)
圧力と水位の時刻歴
case004(maxCo 10.0、maxAlphaCo 10.0)
圧力と水位の時刻歴
case000と比較すると、case003とcase004は結果に違いが出ました。
しかし、case001とcase002で結果に違いが出ません。
おそらくクーラン数縛りの設定をしてますが効いておらず、$\Delta t$が変わっていないからと考えられます。
以下で、クーラン数を時刻歴で確認してみます。
クーラン数の確認
クーラン数の時刻歴変化を見てみます。
クーラン数の出力方法はこちらに書いていますので、ご参考ください。
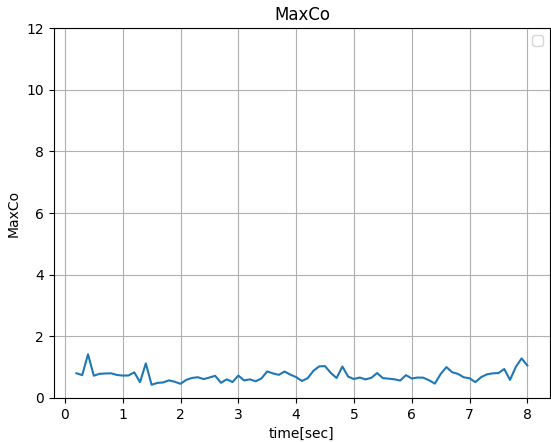
case001(maxCo 5.0、maxAlphaCo0.5)
MaxCo
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
ExecutionTime = 444.67 s ClockTime = 1514 s Courant Number mean: 0.0295328 max: 1.00618 Interface Courant Number mean: 0.00338096 max: 0.459985 deltaT = 0.00583673 Time = 7.99416 PIMPLE: iteration 1 smoothSolver: Solving for alpha.water, Initial residual = 0.000412801, Final residual = 1.09873e-09, No Iterations 2 Phase-1 volume fraction = 0.211769 Min(alpha.water) = -5.868e-07 Max(alpha.water) = 1.00003 MULES: Correcting alpha.water MULES: Correcting alpha.water Phase-1 volume fraction = 0.211769 Min(alpha.water) = -2.6557e-06 Max(alpha.water) = 1.00003 DICPCG: Solving for p_rgh, Initial residual = 0.00262326, Final residual = 5.90619e-05, No Iterations 2 time step continuity errors : sum local = 0.000186976, global = 5.03081e-08, cumulative = 0.00243923 DICPCG: Solving for p_rgh, Initial residual = 9.07816e-05, Final residual = 3.90669e-06, No Iterations 10 time step continuity errors : sum local = 1.23549e-05, global = 1.87299e-06, cumulative = 0.0024411 DICPCG: Solving for p_rgh, Initial residual = 1.23139e-05, Final residual = 7.39855e-08, No Iterations 28 time step continuity errors : sum local = 2.33905e-07, global = 2.68529e-08, cumulative = 0.00244113 ExecutionTime = 444.86 s ClockTime = 1515 s Courant Number mean: 0.0294103 max: 1.02874 Interface Courant Number mean: 0.00336109 max: 0.45668 deltaT = 0.00583673 Time = 8 |
設定は「maxCo 5.0」のはずがずっと1くらいです。
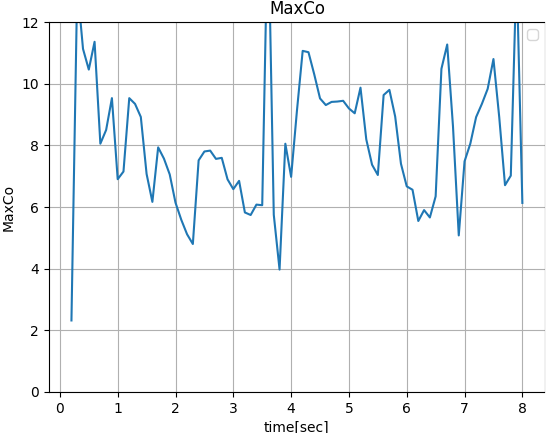
case002(maxCo 10.0、maxAlphaCo 0.5)
MaxCo


こちらも設定は「maxCo 10.0」のはずがずっと1くらいです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
Courant Number mean: 0.0295328 max: 1.00618 Interface Courant Number mean: 0.00338096 max: 0.459985 deltaT = 0.00583673 Time = 7.99416 PIMPLE: iteration 1 smoothSolver: Solving for alpha.water, Initial residual = 0.000412801, Final residual = 1.09873e-09, No Iterations 2 Phase-1 volume fraction = 0.211769 Min(alpha.water) = -5.868e-07 Max(alpha.water) = 1.00003 MULES: Correcting alpha.water MULES: Correcting alpha.water Phase-1 volume fraction = 0.211769 Min(alpha.water) = -2.6557e-06 Max(alpha.water) = 1.00003 DICPCG: Solving for p_rgh, Initial residual = 0.00262326, Final residual = 5.90619e-05, No Iterations 2 time step continuity errors : sum local = 0.000186976, global = 5.03081e-08, cumulative = 0.00243923 DICPCG: Solving for p_rgh, Initial residual = 9.07816e-05, Final residual = 3.90669e-06, No Iterations 10 time step continuity errors : sum local = 1.23549e-05, global = 1.87299e-06, cumulative = 0.0024411 DICPCG: Solving for p_rgh, Initial residual = 1.23139e-05, Final residual = 7.39855e-08, No Iterations 28 time step continuity errors : sum local = 2.33905e-07, global = 2.68529e-08, cumulative = 0.00244113 ExecutionTime = 444.51 s ClockTime = 1514 s Courant Number mean: 0.0294103 max: 1.02874 Interface Courant Number mean: 0.00336109 max: 0.45668 deltaT = 0.00583673 Time = 8 |
maxAlphaCo 0.5縛りによって、maxCoを大きくとれていないですね。
それゆえに、時間刻みも小さいままです。
だから、圧力や水位の時刻歴においてcase000との違いが出なかったということです。
case003(maxCo 5.0、maxAlphaCo 5.0)
MaxCo
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
Courant Number mean: 0.189035 max: 5.03542 Interface Courant Number mean: 0.0210549 max: 3.02185 deltaT = 0.0333333 Time = 7.96667 PIMPLE: iteration 1 smoothSolver: Solving for alpha.water, Initial residual = 0.00184151, Final residual = 1.14069e-09, No Iterations 5 Phase-1 volume fraction = 0.211509 Min(alpha.water) = -6.98059e-05 Max(alpha.water) = 1.00015 MULES: Correcting alpha.water MULES: Correcting alpha.water Phase-1 volume fraction = 0.211509 Min(alpha.water) = -0.000314536 Max(alpha.water) = 1.00133 DICPCG: Solving for p_rgh, Initial residual = 0.00654128, Final residual = 0.000188384, No Iterations 2 time step continuity errors : sum local = 0.0151257, global = -4.8725e-05, cumulative = 0.0422917 DICPCG: Solving for p_rgh, Initial residual = 0.000276112, Final residual = 1.33488e-05, No Iterations 9 time step continuity errors : sum local = 0.00106436, global = 0.000209138, cumulative = 0.0425008 DICPCG: Solving for p_rgh, Initial residual = 7.22407e-05, Final residual = 9.37697e-08, No Iterations 35 time step continuity errors : sum local = 7.45577e-06, global = -2.55728e-07, cumulative = 0.0425006 ExecutionTime = 94.38 s ClockTime = 376 s Courant Number mean: 0.185345 max: 7.24439 Interface Courant Number mean: 0.0200729 max: 1.87555 deltaT = 0.0333333 Time = 8 |
maxAlphaCo 5.0にすることで、maxCoを大きくとれています。
それゆえに、時間刻みも大きめになっています。
時間刻みが大きくなっているので、精度が落ちて圧力P1の時刻歴が実験データと合わなくなってきたということですね。
case004(maxCo 10.0、maxAlphaCo 10.0)
MaxCo
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
DICPCG: Solving for p_rgh, Initial residual = 8.22201e-05, Final residual = 7.73108e-08, No Iterations 35 time step continuity errors : sum local = 5.55676e-06, global = -4.41755e-07, cumulative = 0.0688766 ExecutionTime = 55.53 s ClockTime = 185 s Courant Number mean: 0.224018 max: 6.3044 Interface Courant Number mean: 0.0216694 max: 2.29178 deltaT = 0.0333333 Time = 7.96667 PIMPLE: iteration 1 smoothSolver: Solving for alpha.water, Initial residual = 0.001657, Final residual = 6.00192e-09, No Iterations 5 Phase-1 volume fraction = 0.211218 Min(alpha.water) = -0.00026623 Max(alpha.water) = 1.00001 MULES: Correcting alpha.water MULES: Correcting alpha.water Phase-1 volume fraction = 0.211218 Min(alpha.water) = -0.0044743 Max(alpha.water) = 1.00023 DICPCG: Solving for p_rgh, Initial residual = 0.00711339, Final residual = 0.000217433, No Iterations 2 time step continuity errors : sum local = 0.0159052, global = 6.23523e-05, cumulative = 0.0689389 DICPCG: Solving for p_rgh, Initial residual = 0.000320344, Final residual = 1.39753e-05, No Iterations 9 time step continuity errors : sum local = 0.00101415, global = 0.000230766, cumulative = 0.0691697 DICPCG: Solving for p_rgh, Initial residual = 8.18283e-05, Final residual = 9.68297e-08, No Iterations 35 time step continuity errors : sum local = 7.00384e-06, global = -5.04597e-07, cumulative = 0.0691692 ExecutionTime = 55.75 s ClockTime = 186 s Courant Number mean: 0.218453 max: 6.16746 Interface Courant Number mean: 0.0208167 max: 2.12081 deltaT = 0.0333333 Time = 8 |
こちらもクーラン数については設定どおりです。
時間刻みが大きいですね。
クーラン数のソースコードの確認
OpenFOAMはオープンソースゆえにコードの中身を覗くことができます。
今回はsystem/controlDictのこちらの2つの設定から、どのようにクーラン数を計算しているのかを確認します。
|
1 2 |
maxCo 0.5; maxAlphaCo 0.5; |
CourantNoに詳しく式が書いているので確認。
OpenFOAMは有限体積法なので、差分法のクーラン数$C=\frac{u\Delta t}{\Delta x}$の式と異なりますが、お気持ちは何となくわかりますね。
ソースコードを見ると確かにそのようになっています。
maxCoについて
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
scalar CoNum = 0.0; scalar meanCoNum = 0.0; if (mesh.nInternalFaces()) { surfaceScalarField phiMask(localMin<scalar>(mesh).interpolate(cellMask)); scalarField sumPhi ( fvc::surfaceSum(mag(phiMask*phi))().internalField() ); CoNum = 0.5*gMax(sumPhi/mesh.V().field())*runTime.deltaTValue(); meanCoNum = 0.5*(gSum(sumPhi)/gSum(mesh.V().field()))*runTime.deltaTValue(); } Info<< "Courant Number mean: " << meanCoNum << " max: " << CoNum << endl; |
maxAlphaCoについて
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
scalar maxAlphaCo ( runTime.controlDict().get<scalar>("maxAlphaCo") ); scalar alphaCoNum = 0.0; scalar meanAlphaCoNum = 0.0; if (mesh.nInternalFaces()) { surfaceScalarField phiMask(localMin<scalar>(mesh).interpolate(cellMask)); scalarField sumPhi ( mixture.nearInterface()().internalField() *fvc::surfaceSum(mag(phiMask*phi))().internalField() ); alphaCoNum = 0.5*gMax(sumPhi/mesh.V().field())*runTime.deltaTValue(); meanAlphaCoNum = 0.5*(gSum(sumPhi)/gSum(mesh.V().field()))*runTime.deltaTValue(); } Info<< "Interface Courant Number mean: " << meanAlphaCoNum << " max: " << alphaCoNum << endl; |
合わせて確認しておくと良いでしょう。
まとめ
本記事は気液混相流ソルバinterFoamのクーラン数違いによる結果の比較を行いました。
- 時間刻みを大きくすると精度が落ちるが計算時間は短縮できる。
- 時間刻みを小さくすると、精度は高まるが計算時間が延びる。
彼方立てれば此方が立たぬ。
手元のPCのスペック次第で、どこまで精度を見るか、どれだけ解析時間に工数を割けるかに依って上手く対応する必要がありそうです。
interFoamで$\Deltat=1e-7$とかになったら、他にどんな対処方法があるだろうか?
参考書
PENGUINさんサイトを体系的に学べる書籍となっています。ネット記事でも十分勉強できるのですが、OpenFOAMの初学者でOpenFOAMをインストール済みであれば一冊持って置き、体系的に学ぶのが良いでしょう。
あとは初心者向けに丁寧に解説がされているこちらの書籍もお勧めです。最後の章にはオーバーセットメッシュ(重合メッシュ)の機能を使った解析を最後まで丁寧に解説しているので挫折することはないでしょう。
こちらはFoundation版によるOpenFOAMの辞書的役割を担う参考書ですが、非常に参考になります。