すこ~しづつ「ランダウ=リフシッツ”力学”」を読み進めています(笑)
ここ最近は、「対称性があると保存則があるよ」というのを見てきました。
これは一般的にはネーターの定理と呼ばれるものです(^^)
本記事は
「対称性があると保存則がある」というのをまとめます。
プラス、個人的に思ったことを最後に書いています。
ネーターの定理の説明
ネーターの定理
「系に連続的な対称性がある場合はそれに対応する保存則が存在する」と述べる定理である。
ドイツの数学者エミー・ネーターによって1915年に証明され、1918年に公表された。
解析力学や場の理論における重要な定理であります。
これだけ覚えておけば良いでしょう(^^)/
「対称性が何によるかによって保存則が決まっている」ということです。
具体例まとめ
下記のサイトにひとつひとつまとめました。
| 要請 | 結果 | ↓サイト | |
| 対称性 | 保存量 | ||
| 時間対称性 |
ラグランジアン\(L\)が 時間\(t\)に依存しない |
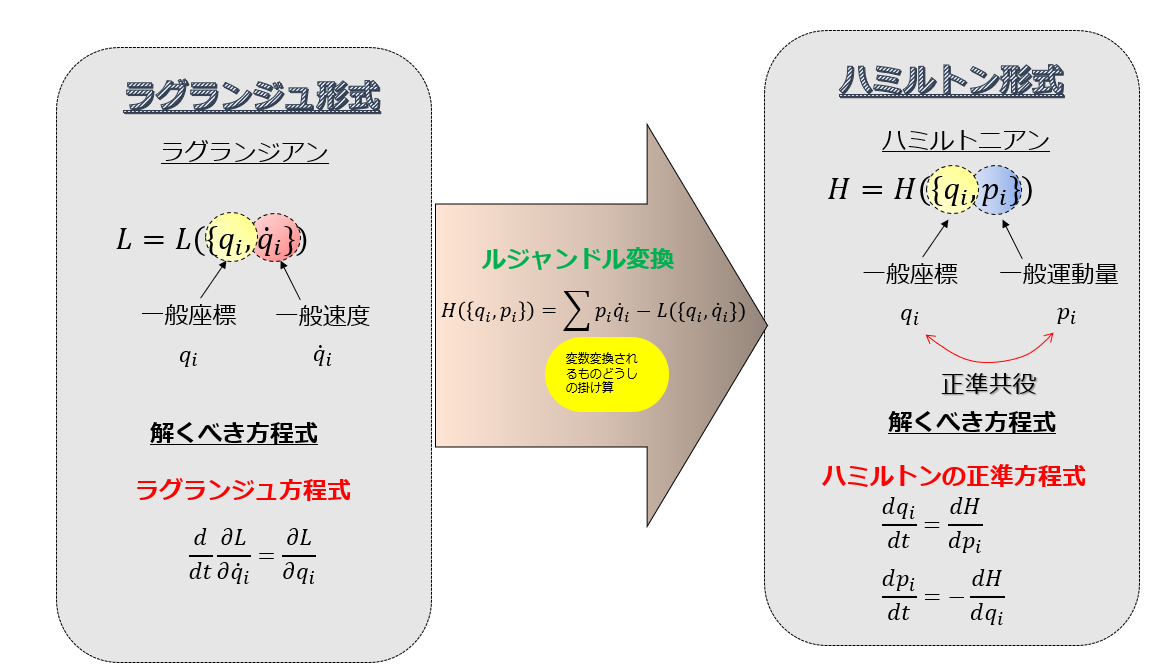
エネルギー保存 \(E=\sum_{i}\frac{\partial L}{\partial \dot{q}_{i}}\dot{q}_{i}-L\) \(\frac{dE}{dt}=0\) |
エネルギー保存則:時間対称 |
| 並進対称性 |
系全体を微小変位\(\epsilon\)だけ動かしても、 ラグランジアン\(L\)が変わらない |
運動量保存則 \(\boldsymbol{P}=\sum_{a}\frac{\partial L}{\partial \boldsymbol{v}_{a}}\) \(\frac{d \boldsymbol{P}}{dt}=0\) |
運動量保存則:並進対称 |
| 回転対称性 |
系全体を微小角度\(\delta \phi\)だけ動かしても、 ラグランジアン\(L\)が変わらない |
角運動量保存則 \(\boldsymbol{M}=\sum_{a}\big(\boldsymbol{r}_{a}\times\boldsymbol{P}\big)\) \(\frac{d\boldsymbol{M}}{dt}=0\) |
角運動量保存則:回転対称 |
見通しが良くなってきました(^^)
次回
上の表のもっと一般的な議論をしたいですね。
つまり、ネータの定理そのものを証明して、「対称性が時間なら・・・エネルギーが保存」、「対称性が並進対称なら・・・運動量が保存」という具合にしたいです。
ところで・・・
気になったことをいくつか挙げます。
ひとつ目
ところで、上記のようで「~の対称性を要請したら」・・・・「~の保存則」が見いだせる・・・
という具合にしましたが、
「~対称性の要請」って誰が決めたのでしょうかね?笑
もし、この要請をしなかったら何も保存則が見いだせないのではないか?と思ってしまいます。
もう少し具体的に言うと、「~の対称性を要請したら」というのは言い換えると、「~の対称性による力学的性質が変わらないとしたら」となります。
逆に、「対称性が要請できない」場合というのはどういった状況でしょうか。
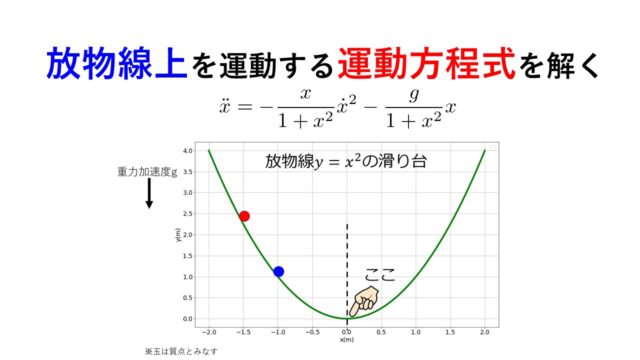
それは運動方程式で考えると余分な項が付いている状態です。
※明示的に\(F\)と書きました。
つまり、余分な項とは外力の事ですね。
ただ、外力が全てそうだとも言えないです。
例えば、もし\(F\)がポテンシャルエネルギーである場合は、
となります。
両辺に\(v=\frac{dx}{dt}\)を掛けると、
となってエネルギーの保存が出ます。
この例だと、明らかにエネルギーは時間に対して依存しない(時間に対して対称である)結果となってしまいました。
ポテンシャルエネルギーでは必然的に対称性を要請している結果となってしまいました。
「対称性が要請できない」場合の良い例が思いつかないですが、明らかなのは\(F(t)\)が時間に依存する場合ですかね。
この場合だと、時間に対してエネルギーは変動するので、エネルギーが時間に対して対称性があるとは言えない状況です。
こんなイメージであっているのだろうか?(笑)
ふたつ目
上記の表が一般的にネーターの定理で証明できるであれば、空間(回転も?)も時間も同等に扱えるということでしょうかね?
そうすると、運動量とエネルギーも同等に扱えるのでしょうかね?
そう言えば、空間も時間も同じ土俵で扱っている分野があったことを思い出しました。
相対性理論です。
相対性理論は詳細は述べませんが、運動量とエネルギーの保存則は、
エネルギー運動量テンソルを用いて統一的に、
と書けたはずです。
ん~・・・・
この辺も少し勉強して記事にしていきたいですね。