本記事
大学受験の物理のための基礎的な考え方を紹介します。
いよいよ新学期が始まりますね。みなさん受験シーズンって本当に嫌ですよね(^^;)
特に苦手な科目の場合、なかなか点数が伸びず足を引っ張ってしまいます。
もしかしてその苦手科目「物理」だったりしますか?
僕は、大学受験で物理を得意科目とし武器にし、某有名私立大学の物理は満点(実は1問間違いだったかも)でありました。
国公立の2次試験でも物理は相変わらずの切り札で、得点源以外の何物でもありませんでした。(逆に「国語」「英語」は散々なものでしたが・・・)
物理は、偏差値でいうと一番貢献している科目でしたね。
(偏差値ってなんだ?って方はこちらをお読みください。。。結構ちゃんと解説しました)
逆にこのように考えている人はいませんか?
物理が嫌い・不得意・・・・でも大学受験で必要だから勉強しないといけない。
もしくは、これから物理を学ぶけど、物理って難しいと聞く・・・
ご安心あれ(^^)
そんなあなたを、僕があなたを救いましょうーーー(^^)
実は物理はとても覚えることが少なく、数学ほど高度な発想がいらないのです。基礎固めから始めればきっと満点(に近い点数)がとれます。
- 物理のお勧め参考書の紹介
- 物理の初学者が一番最初に習う力学の基本方針について解説
※内容が難しくなったかもしれないですが、お勧めの参考書だけでも有益な情報かと(笑)
適切な参考書選び
はっきり言いましょう(^^)
学校の教科書は使ってはいけなません!!!
誤解を生むので、もう少し丁寧に言うと、
学校の「教科書+指導者の指導」があって意味があるのです。
でも、
感覚的に世に出ているわかりやすい参考書は、
「参考書>学校の教科書」
ですので、参考書を買ってしまった方がいいのですよ。
どうして学校の教科書がいけないのかって?
色々書いてあってわけがわからないのです。興味を持つように身近なものに置き換えたりしてるからですかね。
物理の力は問題演習をして感覚が養われていくので、長々と回りくどく説明されては余計複雑に感じてしまいます。
それが学校の教科書なのです。
ちなみに僕は浪人してから物理を学んだので、学校の教科書を読んでいません。
僕が重宝していたのはこちらです。
基礎固め
「物理はイメージだ!」とアドバイスする著者だからこそ、ふんだんに絵を使ってとてもわかりやすく解説しています。
1冊がとても薄く、基本的内容の説明の後にすぐに演習があり、すぐに「物理ができる!!」と実感できる参考書です。
演習問題集
これがとてもいい!!
すべての問題を網羅していると言っても過言ではありません。
そして、難しい問題に対しては穴埋め形式にしてあり、学習している者のハードルをいくぶんか下げてくれて理解がしやすいです。
僕はこの問題集を5周くらいはやりましたね!(^^)!
国公立2次、私立難関校へ
最後はこれで腕試しですね。
これだけ難問題を集めた参考書は少ないので、試験をイメージして腕試ししてはいかがですか。
僕もすべての問題を解いたわけではないですが、少し受験当日をイメージする際には、この問題集を使わせていただきました。
ただ、「絶対全部解かないといけない!!」と意気込んではだめです(笑)
上で挙げた「体系物理をきっちり」やってちょっとこの問題気になる程度に使うのがミソです。
こんな難しい問題を全部するほど受験生は暇ではないですからね。
力学の基本法則は3つだけ
ニュートンの力学の三法則
- 第一法則:慣性の法則
物体が力を受けていない場合、静止しているものは静止し続け、運動しているものは等速直線運動を続ける。- 第二法則:運動方程式\(ma=F\)
物体が力の作用を受けるときは、その力の向きにその大きさに比例した加速度が生じる。- 第三法則:作用反作用の法則
物体が他の物体から力を作用させるとき、その力の向きにその物体から同じ大きさで反対向きに反作用を受ける。
これだけです。
エネルギー保存則とか習ったよという人もいるでしょうが、ご安心ください。
第二法則から導かれたのが、エネルギー保存則です。
(ただ証明はちびっと難しくなるので、後日記事を書きますので乞うご期待(^^))
運動量保存とか習ったよ。
ご安心ください。
第二法則から導かれたのが、運動量保存則です。
(ただ証明はちびっと難しくなるので、後日記事を書きますので乞うご期待(^^))
数学でいうところの内積と深く関わっておりますね。
モーメントの保存とか習ったよ
はいはい・・。
モーメントの保存も第二法則から導かれるんですよ。
(ただ証明はちびっと難しくなるので、後日記事を書きますので乞うご期待(^^))
数学でいうところの外積と深く関わっておりますね。
力のつり合いは??
力が釣り合って物体が止まっているからma=Fのa=0として考えればよろしい。
物理の本質は色々な法則があるけども、
美しいほどシンプルなひとつの法則で理解できるのではないかという探究であると言えます。
なのでそんなに覚えることあってはいけないのです。
ですので、この3つの法則だけで基本物理の問題を解けると思っておきましょう。
電磁気学の問題も?熱力学の問題も?
はい(^^)
基本はこの3つの法則だけですね。
基本はね。
あとはポイントは3つだけ
- 力を矢印で書く 物体同士が接触しているところには必ず力が発生している。
- 力を分解する
- 運動方程式を立てる
法則3つ、ポイント3つってことです(^^)
1.力を矢印で書く
物理の問題を解くときは絶対絵を書きましょう。
逆に絵を描かずに解く問題を教えてほしいくらいです。
だいたい何の絵を描けばいいのかいな?
例:力学の問題
物体が角度θの斜面を滑り降りる時の物体の加速度aを求める問題
物体の質量m、動摩擦係数μ、斜面角度θ、重力加速度g
※空気抵抗なし
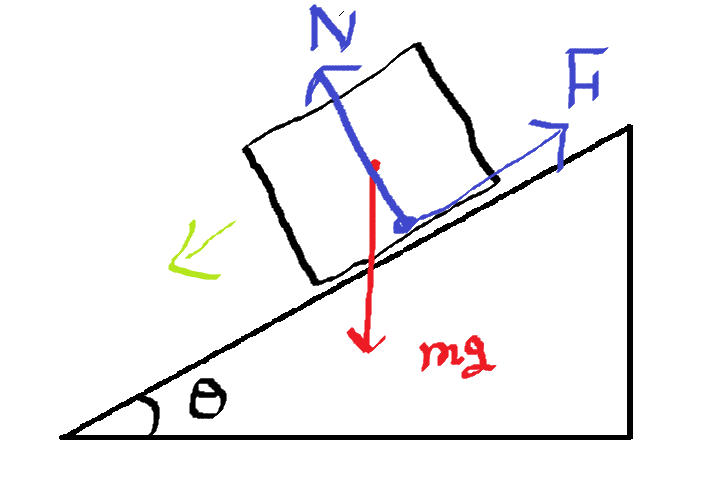
こんな感じの絵ですね。
力の矢印の書き方ですが、どこに力が発生しているか考えないといけないですね。
接触している点には全て力があり
上の絵の青色の矢印で書いたところです。
Nが垂直抗力
Fが摩擦力:動摩擦力は垂直抗力に比例するのでF=μN
2.力は絶対に分解する
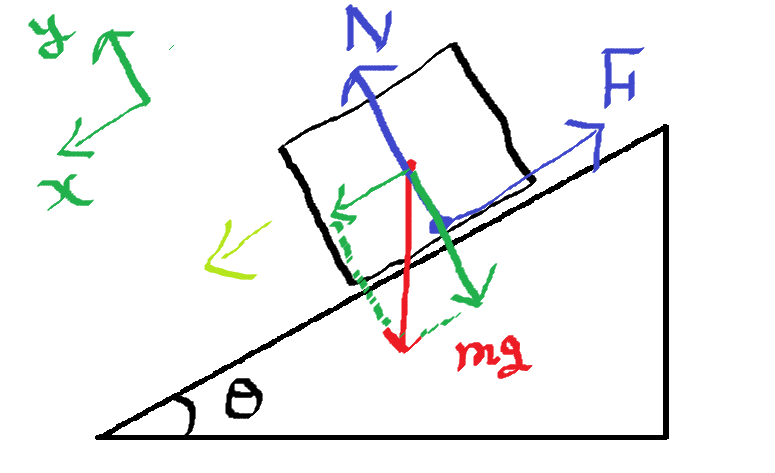
上の絵の緑矢印のように力を分解しましょう。
この後に運動方程式を立てるのですが、運動方程式は各方向に対して式を立てるのが基本です。
数学で言ったらベクトル(方向)の事ですかね。
複雑な問題になると、あっちこっち力の矢印向いているのは考えにくいからです。
上の絵の緑矢印ようにx方向、y方向を分解しても良いですが、2つの直交している向きに分解すれば良いので上の絵でなくても良いです。
自分が解きやすいと思う方向に、矢印を分解しましょう。
基本は、物体が動いている方向に分解すれば問題が考えやすくなります。
3.運動方程式を立てる
さて上の絵で分解したそれぞれの方向(x方向、y方向)で運動方程式を立てたら、後は腕力で解きます。
一応、運動方程式を立てるとこんな感じ
運動方程式
x方向:\(ma=mg\sin\theta-F\)・・・(1)
y方向:\(0=N-mg\cos\theta\)・・・(2)
あとは、
摩擦は、摩擦係数を使って垂直抗力に比例する:\(F=\mu N\)・・・(3)
置いた文字の数(未知数)=立てた方程式の数
であれば方程式は原理的に必ず解ける。
用いた文字は、\(F\)、\(N\)、\(a\)で立てた式は3つなので、あとは腕力でゴリゴリ計算します。
そうすると、加速度\(a\)が求まります↓。
\(a=g\sin\theta-\mu g\cos\theta\)・・・・☆
単位は絶対に確認しておきましょう
上で導き出した答え(☆)くらいなら、全然計算間違いのしようがないですが、物理には単位(次元ともいう)が存在しますので、答え合わせとまではいきませんが、間違っていないかのチェックができます。
上の答え(☆)の場合は、左辺が加速度\(a\)\((m/s^{2})\)・・
であれば右辺も加速度\((m/s^{2})\)の単位のはず。
\(\mu\)と\(\theta\)は無次元量(単位がない)なので、重力加速度\(g\)\((m/s^{2})\)だけが単位となります。
では、左辺と右辺の単位を比較しましょう。
$$左辺の単位=右辺の単位$$
なので答えとしてよさそうです。
これが、\(a=g\sin\theta-\mu mg\cos\theta\)とかだと、変だなってことになりますので、
単位は必ず、ささっとチェックしましょう(^^)/
すべての導いた式について単位を確認する必要はありません。
何度も問題を解いているうちに、不自然な物理量が分母やルートの中に来ていたりすると、答えが間違っているのではないかと疑ってほしいという意味です。
例えば、得られた答えとして・・・
速度\(v\)が、
$$v=\sqrt{2mgh}$$
※\(g\)[m/s2]:重力加速度
※\(h\)[m]:高さ
※\(m\)[kg]:質量
こうなりました。
ここで、「あれ?こんな形になるっけ?」
って思って式を見直すような訓練を日ごろからしておいた方が良いってことです。
「ま~導出過程は複雑だったし、これであっているだろ」って思ったらダメです!!
惜しくも何ともなくて、これに関しては100%答えが間違っています。
※単位を考えたらどれかの文字がいらないですよね。
最後に
いかがですか?
物理は難しく考えてはいけない。
シンプルに考えれば確実に点数が稼げる科目になります。
高校生のみなさんは、新学期が始まりますので、是非物理満点狙ってください(^^)