こんにちは(@t_kun_kamakiri)。
皆さん、偏差値って聞いたことありますよね?
おそらくこの記事を読んでいる方は、偏差値の具体的な計算方法や偏差値の意味について知りたい人だと思います。
そこで・・・・
- 偏差の計算方法を知りたい人
- 偏差値の具体的な計算を知りたい人
- 偏差値の統計学の理論の話を知りたい人
是非、楽しみながら読んでください(^^♪
そこで、本記事の主題
- 偏差値の計算方法
- テストの点数をそのまま語るのが、なぜ公平ではないのか?
- 公平でない要因として、何があるのか?
- 偏差値はどのように計算されているのか?
これらの疑問にお答えしましょう(^^)/
以下の順番で解説を進めていきます。
前半は絵を使いながら非常に丁寧に、後半は数学を使いながらより具体的な計算をしたいと思います。
前半部分で、「へ~」って思っていただければ、よし!!って感じです。
偏差値のイメージ
偏差値が高い=テストの成績が良い
こんなイメージでしょうか。
って言いますけど、ところで・・・
どうしてわざわざテストの点数で言わずに、偏差値で皆さん語るのでしょうかね?
理由は、皆さんも何となくわかっているでしょう(^^)
定量的に公平に判断できるようにもの、
それが偏差値だからですね。
異なる科目や、同じ科目でも異なる集団で受けたテスト(模試が違う)など・・・点数そのものを比較するのはナンセンスです。
偏差値とは
偏差値とはある集団の中での自分の位置を示すものです。
たとえ科目が変わっても(平均点、受験数が異なっても)公平に「あなたは全体でこのくらいの位置にいます」と示しているが偏差値です。
「平均点が低い科目」と「平均点が高い科目」の点数自体をを比較しても、どちらが良い結果なのか判断がでません。
ですので、”統計的にあなたはここくらいの位置にいます”と示してくれるように便利にしたものが偏差値です。
偏差値の計算方法

では、偏差値の計算方法について見てみましょう。
偏差値の計算方法
偏差値=10*(個人の成績 – 平均点)÷(その科目の標準偏差)+50
こちらが偏差値の計算方法です。
テストを受けたとき、個人の成績はわかっていますよね。
偏差値をするために、
- 個人の成績
- 平均点
- 標準偏差
この3つを知り、上の公式に代入すれば偏差値が計算できます!
偏差値の具体的な計算をしてみよう


ここでは、偏差値の具体的な計算を行いたいと思います。
偏差値の計算には以下の2つの統計的な数を使います。
- 平均点
- 標準偏差
標準偏差とは、その科目の「バラツキ具合」を示します。
具体的に計算して理解しましょう!
数学の点数(5人)
| Aさん | 50点 |
| Bさん | 65点 |
| Cさん | 82点 |
| Dさん | 45点 |
| Eさん | 72点 |
平均点
&=\frac{50+65+82+45+72}{5}\\
&=62.8
\end{align*}
上の例だと、平均点:62.8点
標準偏差
&=\frac{(50-62.8)^2+(65-62.8)^2+(82-62.8)^2+(45-62.8)^2+(72-62.8)^2}{5}\\
&=13.7
\end{align*}
上の例だと、標準偏差:13.7
簡単に言うと、「平均点62.8で、13.7点の広がりのある分布」
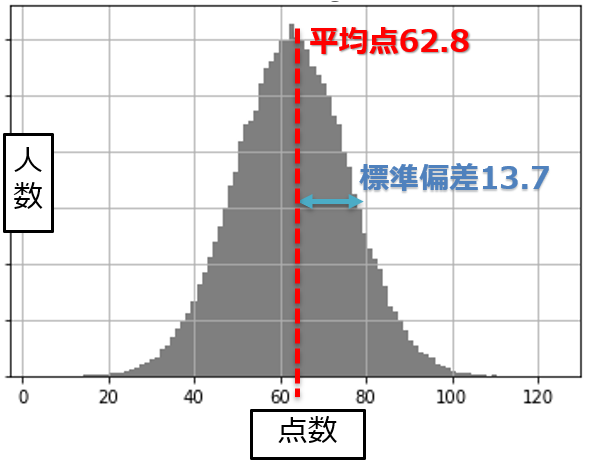
上の例では、サンプル数(人数)が少なすぎるので、本当に分布が上のようなものになるかはかなり怪しいです。
十分な人数がいて、それが正規分布に従っているのであれば、上記のようなグラフ分布であることが望めます。
ですので、偏差値の利用価値が高いのは、サンプルの数値の分布が正規分布に近い状態の時であります。
正規分布ってなんだ?って言う人はこちらをどうぞ。
正規分布
そこで、偏差値の理解しやすくするためにテストの点数の分布が正規分布に従っているとして話を進めます。
※「正規分布でないとどうなるのか?」については最後に少し触れることとします。
偏差値を見ると何がわかる?
ここでは「偏差値の数値を見たら何がわかるのか?」を解説します。
下記のグラフを見てみましょう。
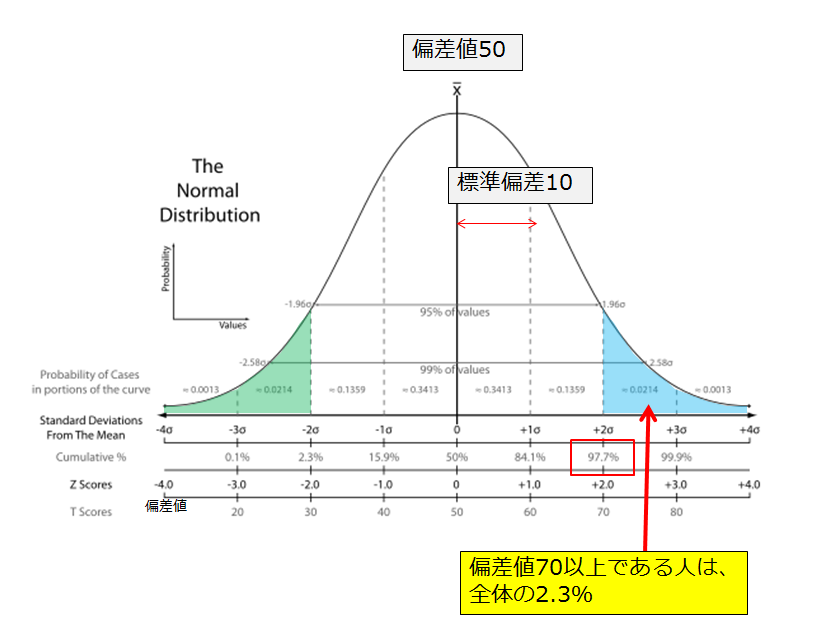

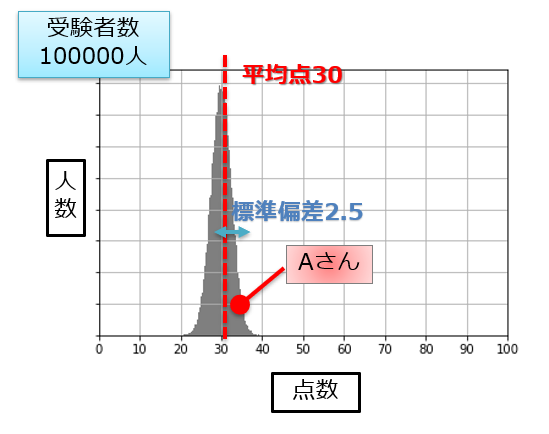
仮に、「偏差値が70以上である」と言っている人がいるとします。
上のグラフは、偏差値70以下の人で97.7%を占めています。
言い換えると、偏差値が70以上の人はその集団の中のわずか2.3%以内に入っている!!
1000人いたら20位くらいってことです。
おー、すごいのかすごくないのか(笑)
優秀な部類ではありますね。
偏差値を導入する理由
続いて偏差値を導入する理由を解説します。
逆に、偏差値という指標がない場合に何が起こるのかを見ればわかるかと思います。
2人の人がこんな会話をしてたとします。


Bくんの受けた試験での分布(●がBくん)



こういう分布を見せられると、Aさんの方が全体の中で優れているように見えます。
では、具体的に数値で表す(偏差値)にはどのようにすればよいかを以降で解説します。
公平でなくしている要因は?
- 人数
- 幅
- 平均値
これらが違う二つのテストの点数自体を比較するのはナンセンス!!
平均点も違うし受けている人数も違うのでは、比較のしようがありません。
平均点が違うと比較しても意味がないのはわかりやすいですが、
仮に平均点が同じであっても、受けている人数が違うだけで、分布は変わります。
たとえば人数が多いと分布は平均点のまわりでシャープになります。
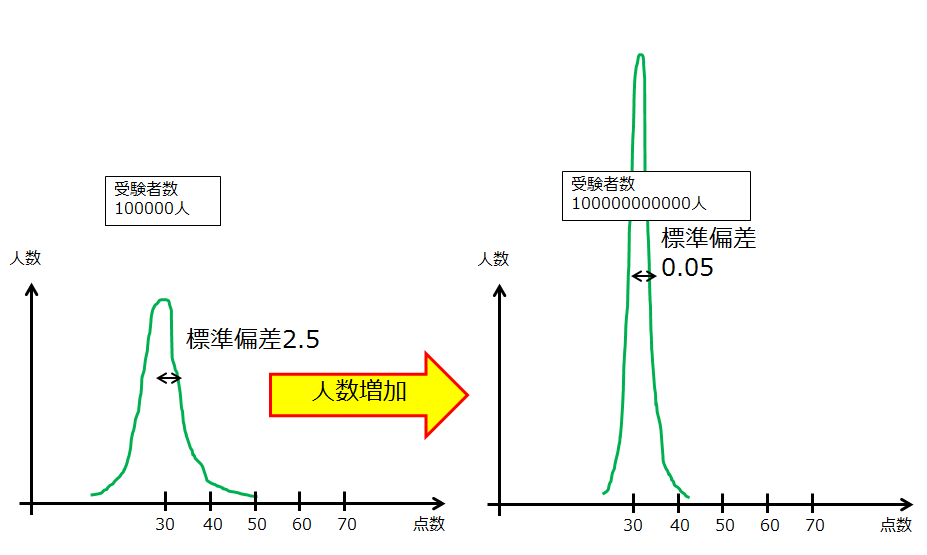

※標準偏差はあくまで例です。
人数が多いだけで標準偏差が小さくなるという意味です。
「平均点のまわりで人数が多いので、そこが際立つ」と考えても良いですし、
標準偏差が\(\sigma=\sqrt{\frac{1}{N}\sum_{i=1}^{N}(x_{i}-\mu_{x})^{2}}\)なので、サンプル数Nが多くなると標準偏差は小さくなるというようにも理解できます。
これらを公平に判断できるように条件でそろえて数値として判断できるようにしたのが偏差値です。
ここでいう「条件をそろえる」とは、決まり事を決めるということです。
公平にするための決まり事を決めよう
では、偏差値とはどのように計算するのでしょうか?
偏差値の計算方法は以下の3点を抑えておく必要があります。
- 人数をそろえる ➡ 合計が1
- バラツキ具合(幅)をそろえる ➡ 標準偏差を10
- 平均値をそろえる ➡ 平均値50
これが偏差値の計算のポイントです。
以上で、偏差値の具体的な計算方法のお話は終わりです(^^)/
偏差値について計算方法も含めて理解が深まったかと思います。
次から、テストの分布が正規分布に従うとして、上記の3条件になるように統計学の理論を使ってガシガシ式変形していきます。
さてここらで、前半戦の終了です(^^)/
このあとは、数式だらけです!
それでは、後半戦にいきます↓
テストの分布を正規分布だと思って分布を正規化しよう

偏差値の計算方法ですが、もう一度おさらいしておきます。
偏差値=10*(個人の成績 – 平均点)÷(その科目の標準偏差)+50
こちらの計算方法はどうやって出てきたのかは気になりますよね。
ここで、統計学の知識を使って「偏差値の計算方法」がどうやって導出されたのかを示したいと思います。
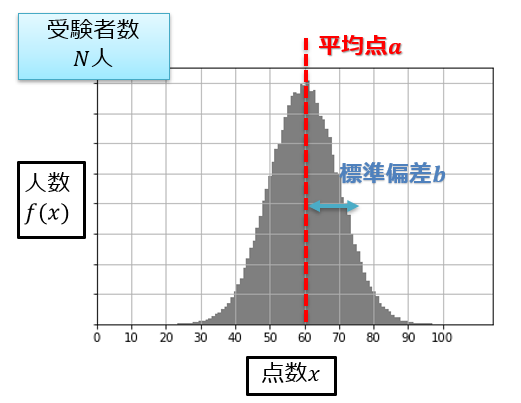

さて、上記のような分布があり、これが正規分布に従っているならば、
f(x)=N\frac{1}{\sqrt{2\pi b^2}}e^{-\frac{(x-a)^{2}}{2b^{2}}}
\end{align*}
と書けます。
ちゃんと、\(N=\int_{-\infty}^{\infty}f(x)dx\)となっていることを各自ご確認下さい。
(人数を積算すると、合計人数である)
そこで、上記3条件「合計が1」「標準偏差が10」「平均値が50」となっている関数を\(g(X)\)とすると、
1=\int_{-\infty}^{\infty}g(X)dX\tag{1}
\end{align*}
となっているはずです。各自確かめてみましょう。
※\(x\)ではなく\(X\)(大文字)ですので注意。
つまり、
$$g(X)=\frac{1}{\sqrt{2\pi \sigma^2}}e^{-\frac{(X-\mu)^{2}}{2\sigma^{2}}}$$
※後で\(\mu=50\),\(\sigma=10\)とします。
となっているように、\(f(x)\)を\(g(X)\)に変換したい。
分布\(f(x)\)の幅も高さも変えて、\(g(X)\)にするのですから、
$$g(X)=Cf(x)$$
とおいて(1)を満たすような、\(X\)や\(C\)を決めるのもよいです。
ここでは簡単に以下のようにして\(X\)や\(C\)を決めます。
\(f(x)\)の条件として、
がありました。
(2)の両辺をNで割って、\(1=\int_{-\infty}^{\infty}\frac{1}{N}f(x)\frac{dx}{dX}dX\)とします。
※\(dX=\frac{dx}{dX}dX\)としました。
(1)式の\(1=\int_{-\infty}^{\infty}g(X)dX\)と比較すると、
であることがわかります。
この(3)式を満たすような、\(x\)と\(X\)の関係は何かを考えます。
であることから、指数部分の\(\frac{X-\mu}{\sigma}=\frac{x-a}{b}\)とすれば(3)式を満たしそうですよね。
一応、(3)式の右辺に代入して左辺と等しくなるかを確認してみます。
ちゃんと(3)の等式が成り立っています。
ゆえに、
あるテストの点数の分布\(f(x)\)を
- 人数をそろえる ➡ 合計が1
- バラツキ具合(幅)をそろえる ➡ 標準偏差を10
- 平均値をそろえる ➡ 平均値50
となるような分布\(g(X)\)を得るために、\(\frac{X-\mu}{\sigma}=\frac{x-a}{b}\)、すなわち
と変換すれば、偏差値\(X\)が計算できる。
※\(\mu=50\)、\(\sigma=10\)
おー!!
序盤で言った、
偏差値=10*(個人の成績-平均点)÷(その科目の標準偏差)+50
これではないか!!
これで「偏差値の計算方法」を統計学から導けましたね(^^)
2人の生徒はどちらが偏差値が高いか?
さて、先ほど例に出した「Aさん」と「Bくんの」偏差値を計算してみましょう。



Aさんの偏差値=\(\frac{10\times(38-30)}{2.5}+50=82\)
なんと偏差値82(笑)
Bくんの受けた試験での分布(●がBくん)



Bくんの偏差値=\(\frac{10\times(50-60)}{10}+50=40\)
偏差値40(笑)
正規分布でない場合は偏差値の利用価値は小さい?
さきほどから正規分布でお話を進めてきましたが、正規分布でない場合は偏差値そのものの利用価値がとても薄くなります。
2つ山がある場合(「優秀な集団」と「おばかさん集団」を集めてテスト)
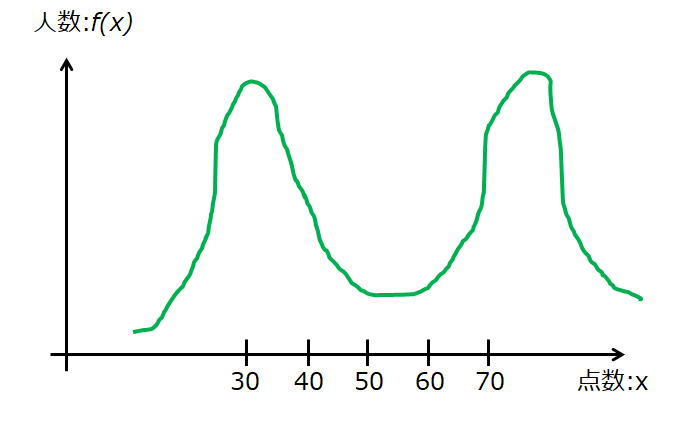

成績上位にいくにつれて一定数になってい場合
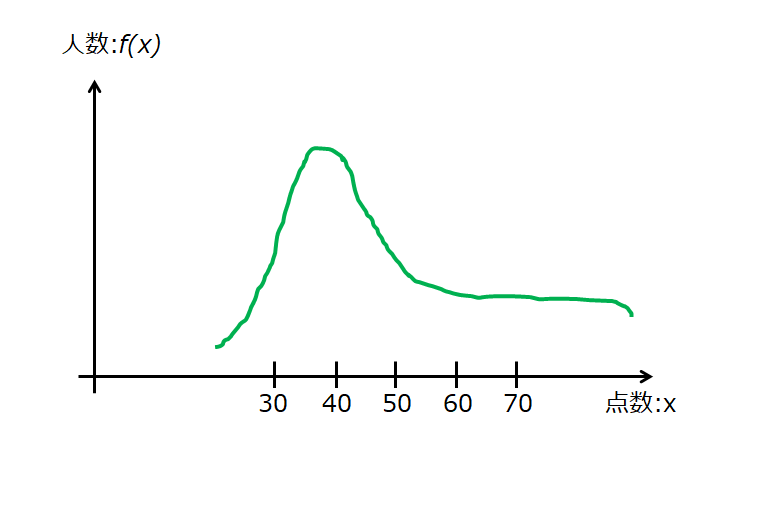

こういった場合は、正規分布ではないので上での式変形などが意味がないですね。
「統計的にあなたはここくらいの位置にいます」という解釈ができなくなります。
偏差値100とったらすごい?
満点とっても偏差値100になるケースの方が稀です。
偏差値100をとったら、むしろ「あなたがその集団に適していなかった」という見方もできます。
たとえば偏差値は学校内でもできるし、小規模であっても偏差値は原理的に計算は可能です。
塾のあるコース内でのテストで偏差値85など出た場合はどうすれば良いのかというと、すぐにその集団が自分にとって適した場所じゃないと考えてもうひとつ上のコースに移ることを進めます(‘ω’)ノ
まとめ
偏差値は世代を超えて利用価値が高い数値であると言えますが、あくまでも「その集団におけるあなたの位置はどこか?」というものになりますので、どのような集団でのテストの偏差値かは非常に重要です。
上を見ればキリがないですが、大手予備校の模試のテストで偏差値で70以上であれば、あなたは受験者の中で相当稀な存在(優秀)であるということです。
逆に偏差値30以下の人も相当レアな存在です(笑)
くれぐれも「勉強してないのに偏差値20もあった」なんて言わないように(笑)
「勉強していないから偏差値20だった」と言いましょう!!
その場合はテストの点で言うと、「0点」である可能性もあります(笑)
おすすめの参考書
偏差値を理解するためには統計学を学ぶ必要があります。
数冊おすすめの参考書を挙げておきたいと思います。
こちらは高校の予備校講師が書いた大学向けの統計学の参考書ですが、大学数学レベルの内容を書きつつ高校生でもわかるように解説した奇跡の参考書です!
↓Python統計分析入門
統計学がは使ってこそ理解が深まるものだと思われます。
同時にPythonというプログラミング言語を学びつつコードを書いて統計学に触れれば学習効果は抜群です。































[…] 【偏差値とは何か】をわかりやすく解説!!「偏差値70以上」は受験者の中でとても優秀!! こんにちは(@t_kun_kamakiri)。 皆さん、偏差値って聞いたことありますよね? 偏差値が高 […]