☆本記事☆
下記の記事で「バスケットボールは45°で投げれば飛距離が伸びるよ」という話をしました。
本記事では、その内容をプログラミング言語Pythonを使って検証をします。
僕のパソコンの環境
Windows10
python3.6.4
Pythonを使った結果
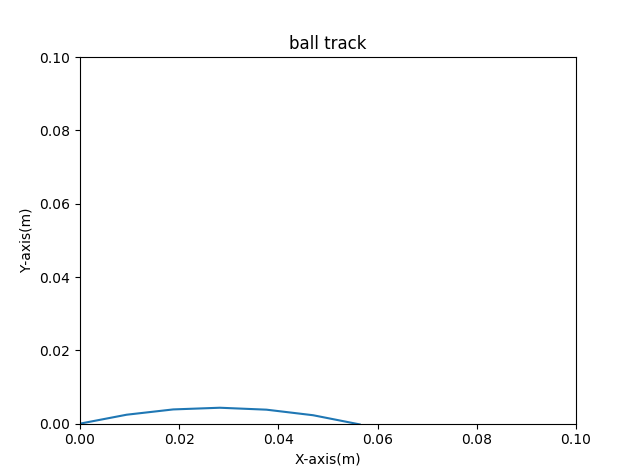
投げ角度20°の軌跡
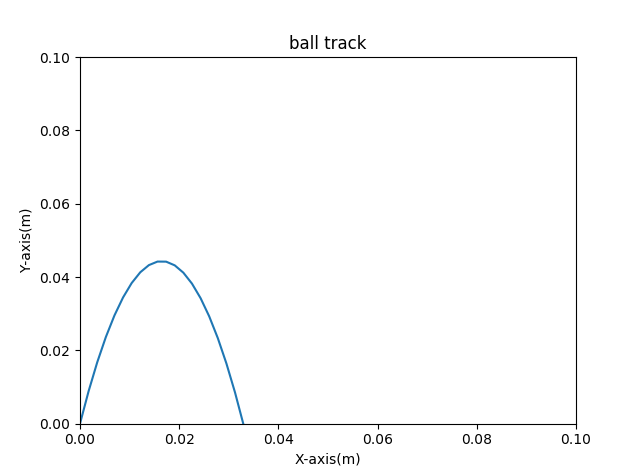
投げ角度80°の軌跡
そして・・・・
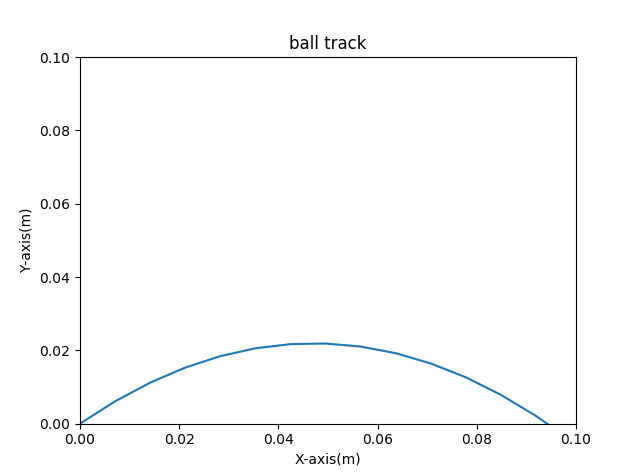
投げ角度45°の軌跡
おお!!めっちゃ飛びますね(笑)
以上です(^^)/
本当は、投げ角度45°が一番飛ぶことを、繰り返し計算でグラフィカルに示したかったのですが、
Pythonは見習い程度なので今日はこんなところで。
また、プログラムが書けたらアップします。
本記事で使ったPythonコードを記載しておきますので、ご自由に改良して下さい。
Pythonコード
Pythonがインストールされていれば、下記のコードを使用することで計算実行できます。
※外部モジュールである「numpy」と「matplotlib」もインストールしておく必要があります。
※下記のプログラムはPython3系での書き方ですので、Python2系をお使いの方はご注意ください。
インストールをしていない人は、本記事の後半をご参照ください。
※文字コードはUTF-8
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 |
""" ある角度θで投げた時の飛距離の計算 """ import math import numpy as np import matplotlib.pyplot as plt #重力加速度 g=9.87 #初期時刻 t=0.0 #時間刻み delta_t=0.01 #y方向の初期高さ y=0.0 #x方向の初期位置 x=0.0 #初速度 v=1.0 #投げる角度θ sita=float(input("投げる角度θの入力:")) #角度をラジアンに変換 rad=math.radians(sita) vx=v*np.cos(rad) vy=v*np.sin(rad) print("現在の位置:",x) print("現在の高さ:",y) print("初速度:",v) #リスト化する tlist=[t] xlist=[x] ylist=[y] #高さyが0以下になるまで計算を繰り返す while y>=0: t+=delta_t vy-=g*delta_t x+=vx*delta_t y+=vy*delta_t #リストに追加 tlist.append(t) xlist.append(x) ylist.append(y) #グラフの表示 plt.plot(xlist,ylist) plt.legend() plt.xlim([0,0.1]) plt.ylim([0,0.1]) plt.title("ball track") plt.xlabel("X-axis(m)") plt.ylabel("Y-axis(m)") plt.show() |
pythonのインストール
↓Pythonは下記のサイトを参照にインストールしましょう。
↓Pythonのおおもとのインストールサイトは下記になりますので、何も参考にしなくてもできる人はこちらから直接アクセスしてインストールしてください。
https://www.python.org/downloads/
外部モジュール「numpy」と「matplotlib」のインストール
本記事で使ったプログラムの中には、外部モジュールである「numpy」と「matplotlib」がインポートされています。
そちらをPythonのインストールが完了したら合わせてインストールしておく必要があります。
↓参考になるサイトのリンクを書きに示しておきます。
(1)numpyのインストール
https://qiita.com/kenichi-t/items/7319b3876ae7f0d3817c
(2)matplotlibのインストール
https://qiita.com/Morio/items/d75159bac916174e7654