どうも(@t_kun_kamakiri)(^^)/
自宅でCAE解析をしたいと思ったことはありませんかね?
そんな人には・・・・
フリーのCAE解析ソフトElmerがおすすめです♪
このフリーソフトのCAE解析ソフトElmerを使って、自宅で無料でCAE解析を行いたいと思います。
※こちらの記事を読んでいることが大前提です(^^)/
CAE解析の中でも、本記事は流体解析について紹介したいと思います。
- 趣味で流体解析を自宅でしたい人
- Elmerを使ってみたいけど使い方がわからない人
本記事のElmerを使った解析結果はこんな感じです↓

※PCの環境
- Windows10
- Intel Core i7@2.50GHz 2.6GHz
- メモリ8G
※Elmerのversion
- Elmer 8.3
Elmerのホームページから理論解説のドキュメントを入手
Elmerに関するドキュメントはホームページのこちらから入手することができます。
↓ホームページ
https://www.csc.fi/web/elmer
Elmerのチュートリアル9:バックステップ流れ
ここからはElmerのチュートリアルを参考に、バックステップ流れをやっていきたいと思います。
↓下記のドキュメントのP.45を参考にしてください。
http://www.nic.funet.fi/pub/sci/physics/elmer/doc/ElmerTutorials.pdf
バックステップ流れとは?
バックステップ流れというのは、左から流れ場が入ってきて途中で段差がある場合に、段差の後ろで渦ができるような流れのことを言います。

段差で流れが壁から剥がれて、段差の後ろで渦ができ、ある距離進むとまた壁に沿って流れるようになります。
しかし、レイノルズ数が小さいような層流的な流れでは、渦は生成しにくいので解析条件としては十分大きなレイノルズ数になるように設定しておく必要があります。
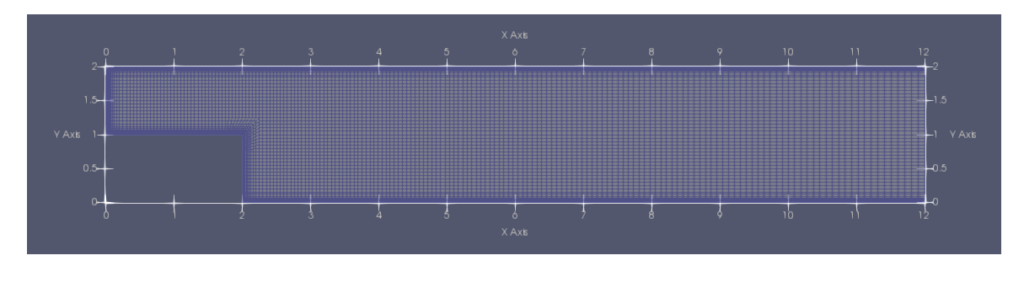
解析条件
- サイズとメッシュ
解くべき方程式
運動量保存則
\rho(\vec{u}\cdot\nabla)\vec{u}=-\nabla p +\nabla\cdot\big(2\mu\bar{\bar{\epsilon}}\big)\tag{1}
\end{align*}
\epsilon_{ij}=\frac{1}{2}\bigg(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\bigg)\tag{2}
\end{align*}
質量保存則
\nabla\cdot \vec{u}=0\tag{3}
\end{align*}
※↑これは密度変化を考慮しないという仮定から導かれた非圧縮仮定の式ですね。
境界条件
流入条件(inlet):\(v_{x}=6(y-1)(2-y)\)

その他の条件
- 乱流モデル無し
- 定常解析
- 粘性係数:0.01[Pa⋅s=kg/m s]
- 密度:1.0[kg/m3]
- 2次元の解析
レイノルズ数
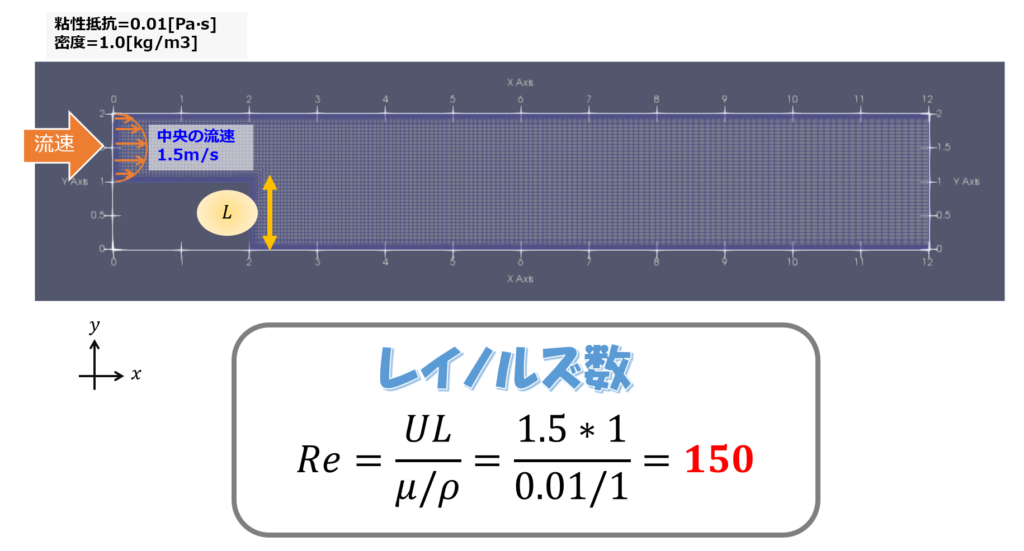
レイノルズ数は150とかです。
操作方法の動画
これを見て皆さんもCAE解析を自宅でお楽しみください・・・・
まとめ
今回は、フリーのCAE解析ソフトElmerを使って流体解析を自宅のPCで行ってみました。
感想は、英語ですがドキュメントが豊富でチュートリアルも充実しているので無償とは思えないほど簡単に流体解析を体験することができました。
【メリット】
- 理論解説とチュートリアルが充実しているので簡単にCAE解析が体験できる。
(サンプルモデル有) - 基本はGUIでの操作での設定なので、初心者のハードルを下げている。
- CAE解析がタダでできる。
【デメリット】
- 日本語のドキュメントが少ない(ほとんどない)。
- GUIはあるが解析設定がフローのようになっていないので少しわかりづらい。
- 複雑な設定はまだ他の商用ソフトに比べると少ないです。
今後はこのような使いやすくて、無料でCAE解析ができるツールが増えていってほしいなと思います。










[…] 領域は計算の検証のため、カマキリさんの記事の計算結果と合わせました。 […]
大変有益な情報をありがとうございます。初心者向けに丁寧に解説があって素晴らしいです。
コメントありがとうございます。
お役に立てたようで嬉しいです。
今後ともよろしくお願いいたします。