こんにちは(@t_kun_kamakiri)(‘◇’)ゞ
本内容は、「比熱の温度依存性の理解のため」のための記事です。
シリーズ化していますので「なぜ比熱に温度依存性があるのか?」を知りたい方は、以下のシリーズを読んで頂ければ理解できると思います。
量子力学における基礎式であるシュレディンガー方程式を使うことになります(^^)/
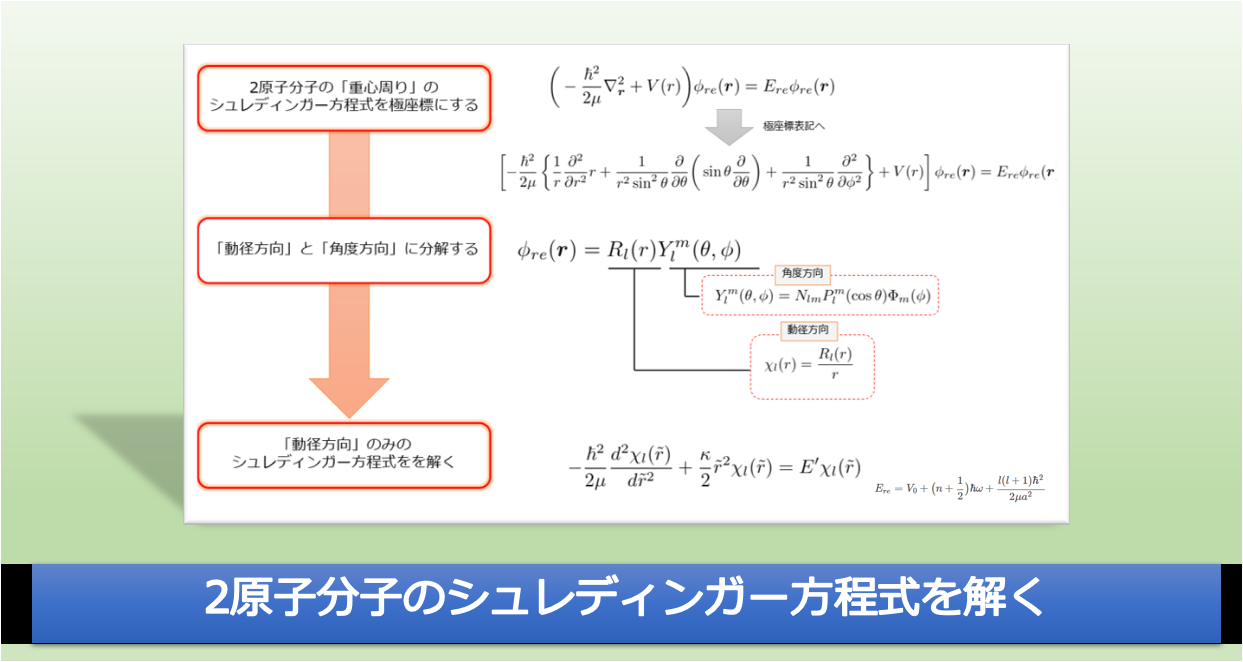
今回の記事では「2原子の分子のシュレディンガー方程式」の形式を示すだけにとどめて、具体的にシュレディンガー方程式を解く過程というのは次回の記事で解説したいと思います。
本記事を読むにあたって詳細の計算まで踏み込んで議論していては、時間がかかりすぎるため前提にしている知識が3つあります。
- 古典力学
- 統計力学(平衡)
- じゃっかんの量子力学の知識
前回の復習:古典統計力学の近似を使って比熱を計算した
まずは前回の復習をさらっとやりましょう。
前回は何をやったかというと、「古典統計力学の近似(準古典近似)」を使って、2原子分子の運動(「重心運動」「2原子間の振動運動」「重心周りの回転運動」に分解)による分配関数を計算し、比熱を求めました。
| エネルギー | 自由度 | |
| 重心運動 | 重心の並進運動エネルギー \(\frac{\boldsymbol{p_{M}}^2}{2M}\) |
3 |
| 2原子間の振動運動 | 運動エネルギー+振動エネルギー \(\frac{p_{r}^2}{2\mu}+\frac{\kappa^2}{2}r^2\) |
2 |
| 重心周りに回転運動 | 回転運動エネルギー \(\frac{1}{2I}\bigg(p_{\theta}^2+\frac{p_{\phi}^2}{\sin^2\theta}\bigg)\) |
2 |
自由度は「位置」or「運動量」の2乗の項が何個あるのかで決まっています。
2原子分子の自由度\(f\)が、\(f=7\)なので、
比熱は\(c=\frac{f}{2}k_B=\frac{7}{2}k_B\)
という結果になります。
といった。。。以上が、量子論を用いない場合(古典論)での話での結果であります。
今回から、量子論を使って比熱を計算していく手順を解説していきたいと思います(^^)/
比熱を求めるまでの手順(今回はおさらいだけ)
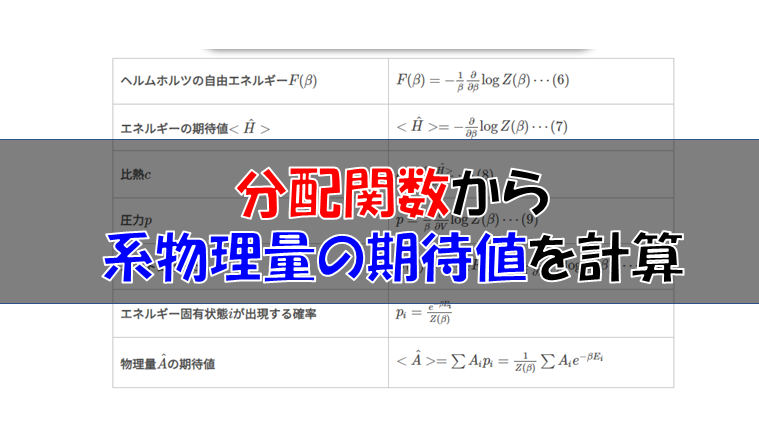
統計力学において物理量の期待値を求めるための手順は、古典論(準古典近似)でも量子論でも同じです。
以下の手順を必ず踏みます。
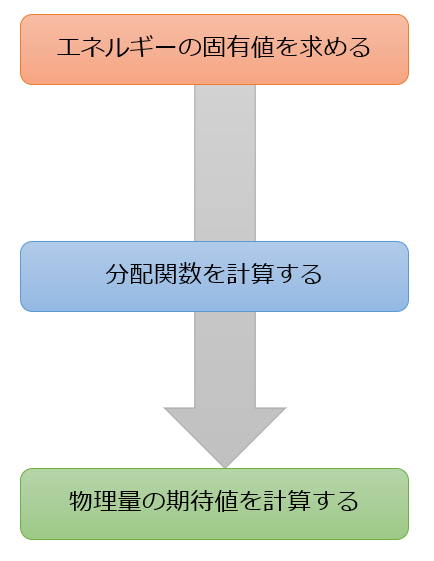

分配関数を求めることができれば物理量の期待値は求めることができるのですね(‘ω’)
分配関数を求めるためには、エネルギー固有値(準古典近似の場合はハミルトニアンそのもの)を知れば良いということになるので、さっそくエネルギー固有値を計算してみましょう。
エネルギー固有値はシュレディンガー方程式を解くことで得られる
といっても、エネルギー固有値を求めるためには解くべき方程式が明確でないといけません。
今回は2原子分子のシュレディンガー方程式を記述するところから始めます。
(というかこの記事ではそれしかしません。)
では、シュレディンガー方程式はどのように作れば良いのかというと・・・
以下のように波動関数\(\psi\)にハミルトニアン演算子を作用させたときに出てくる固有値を求めるという式を立てることでシュレディンガー方程式が作られます。
\hat{H}\psi=E\psi
\end{align*}
このように量子力学的な取り扱いを行うためにはハミルトニアン\(H\)も量子力学での演算子\(\hat{H}\)として扱う必要があります。
量子力学的な取り扱いというと何だか難しいそうだなと思うかもしれませんが、難しいことは考えずに高校物理から馴染んでいる古典力学から量子力学への変更は、以下の手続きを踏むだけだということを覚えておきましょう(^^)/
とするだけで、古典力学から量子力学への取り扱いに変更したことになります。
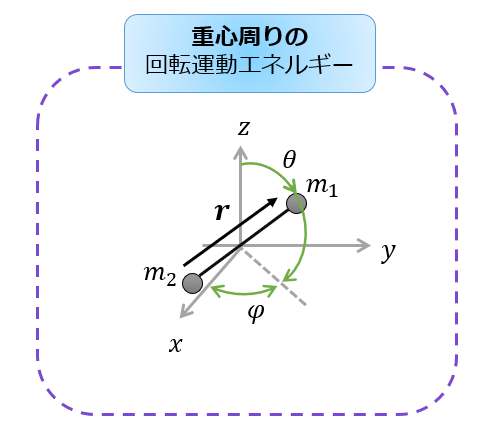
では、まず古典力学での2原子分子のハミルトニアンを書いてみます(これは前回の記事の内容と同じです)
H=\frac{|\boldsymbol{p^{(1)}}|^2}{2m_{1}}+\frac{|\boldsymbol{p^{(2)}}|^2}{2m_{2}}+V(q)\tag{1}
\end{align*}
- 重心の質量:\(M=m_1+m_2\)
- 重心のベクトル:\(\boldsymbol{r_{M}}=\frac{m_1\boldsymbol{r}_{1}+m_2\boldsymbol{r_{2}}}{m_1+m_2}\)
- 相対位置:\(\boldsymbol{r}=\boldsymbol{r_{1}}-\boldsymbol{r_{2}}\)
※\(q=r\) - 換算質量:\(\mu=\frac{m_1 m_2}{m_1+m_2}\)

古典論でのハミルトニアン
古典論での2原子分子のハミルトニアンは、
H &= \frac{|\boldsymbol{p^{(1)}}|^2}{2m_{1}}+\frac{|\boldsymbol{p^{(2)}}|^2}{2m_{2}}+V(q) \\
&= \frac{|\boldsymbol{p_{M}}|^2}{2M}+\frac{|\boldsymbol{p_{re}}|^2}{2\mu}+V(q) \\
&=H_{M}+H_{re}\tag{2}
\end{align*}
となります。
2つ目の式で「重心運動に依るハミルトニアン」と「重心周りの相対運動のハミルトニアン」に分解しました。
「重心運動に依るハミルトニアン」
H_{M} =\frac{|\boldsymbol{p_{M}}|^2}{2M}\tag{3}
\end{align*}
「重心周りの相対運動のハミルトニアン」
H_{re}=\frac{|\boldsymbol{p}|^2}{2\mu}+V(q)\tag{4}
\end{align*}
これにて古典力学でのハミルトニアンを知ることができました。
量子論でのハミルトニアンに変更する
量子力学への変更の手続きは、運動量に対して運動量演算子に変更する(\(\hat{p}\rightarrow -i\hbar\nabla\))だけですね。
「重心運動に依るハミルトニアン」量子力学的取り扱い
H_{M} =\frac{|\boldsymbol{p_{M}}|^2}{2M}\rightarrow-\frac{\hbar^2}{2M}\nabla_{\boldsymbol{R}}^2\tag{5}
\end{align*}
「重心周りの相対運動のハミルトニアン」量子力学的取り扱い
H_{re}=\frac{|\boldsymbol{p}|^2}{2\mu}+V(q)\rightarrow -\frac{\hbar^2}{2\mu}\nabla_{\boldsymbol{r}}^2+V(r)\tag{6}
\end{align*}
つまり、
\hat{H} &=\hat{H}_{M}+\hat{H}_{re}\\
&=-\frac{\hbar^2}{2M}\nabla_{\boldsymbol{R}}^2-\frac{\hbar^2}{2\mu}\nabla_{\boldsymbol{r}}^2+V(r)\tag{7}
\end{align*}
となります。
今から何をしたいかというと、ハミルトニアンからエネルギー固有値を得たいのですよね。
そのためには、量子力学的な状態変数\(\Phi(\boldsymbol{r})\)にハミルトニアン演算子を作用させることで、エネルギー固有値を求めることができます。
\hat{H}\Phi(\boldsymbol{r})=E\Phi(\boldsymbol{r})\tag{8}
\end{align*}
重心運動と相対運動に分けると以下のようになります。
\bigg(\hat{H}_{M}+\hat{H}_{re}\bigg)\Phi(\boldsymbol{r})=\bigg({E}_{M}+{E}_{re}\bigg)\Phi(\boldsymbol{r})\tag{9}
\end{align*}
全エネルギーを「重心の並進運動エネルギー固有値」と「重心周りのエネルギー固有値」に分けました。
\underset{全エネルギー}{\underline{E}}=\underset{重心の並進運動エネルギー固有値}{\underline{E_M}}+\underset{重心周りのエネルギー固有値}{\underline{E_{re}}}
\end{align*}
ハミルトニアン演算子の重心に対する微分\(\nabla_{\boldsymbol{R}}\)と、相対位置に対する微分\(\nabla_{\boldsymbol{r}}\)は独立であるため、以下の交換関係が成り立ちます。
[\hat{H}_{M},\hat{H}_{re}]=\hat{H}_{M}\hat{H}_{re}-\hat{H}_{re}\hat{H}_{M}=0\tag{10}
\end{align*}
ということは、
[\hat{H},\hat{H}_{M}]=[\hat{H},\hat{H}_{re}]=0\tag{11}
\end{align*}
(10)(11)式が何を意味しているのかというと、ハミルトニアン演算子\(\hat{H}\)と\(\hat{H}_{M}\)と\(\hat{H}_{re}\)に対する同時固有関数が存在するということです。
つまり、
\left\{\begin{matrix}
\hat{H}\Phi=E\Phi\\
\hat{H}_{M}\Phi=E_{M}\Phi\\
\hat{H}_{re}\Phi=E_{re}\Phi
\end{matrix}\right.\tag{12}
\end{align*}
と書けるわけですね。
※\(E=E_M+E_{re}\)
このように書けるとき、シュレディンガー方程式\(\hat{H}\Phi=E\Phi\)の解は、
\Phi=\psi_{M}(\boldsymbol{R})\phi_{re}(\boldsymbol{r})\tag{13}
\end{align*}
と変数分離できる解を持ちます。
※実際に(13)式を(12)式に代入して確かめてください。
変数分離した解(13)式を用いると、
「重心運動に依るハミルトニアン」量子力学的取り扱い
\hat{H}_{M}\psi_{M}(\boldsymbol{R}) & =& E_{R}\psi_{M}(\boldsymbol{R})\\
\Leftrightarrow \\
-\frac{\hbar^2}{2M}\nabla_{\boldsymbol{R}}^2\psi_{M}(\boldsymbol{R}) &=& E_{R}\psi_{M}(\boldsymbol{R}) \tag{14}
\end{align*}
「重心周りの相対運動のハミルトニアン」量子力学的取り扱い
\hat{H}_{re}\phi_{re}(\boldsymbol{r}) & =& E_{re}\phi_{re}(\boldsymbol{r})\\
\Leftrightarrow \\
\bigg(-\frac{\hbar^2}{2\mu}\nabla_{\boldsymbol{r}}^2+V(r)\bigg)\phi_{re}(\boldsymbol{r}) &=& E_{re}\phi_{re}(\boldsymbol{r}) \tag{15}
\end{align*}
これで、偏微分方程式になったので(12)(13)式を解くことで、エネルギー固有値\(E_M\)と\(E_{re}\)を求めることができます。
まとめ
今回は、2原子分子のハミルトニアン演算子\(\hat{H}\)、
\hat{H} &=\hat{H}_{M}+\hat{H}_{re}\\
&=-\frac{\hbar^2}{2M}\nabla_{\boldsymbol{R}}^2-\frac{\hbar^2}{2\mu}\nabla_{\boldsymbol{r}}^2+V(r)\tag{7}
\end{align*}
におけるシュレディンガー方程式を「重心運動」と「重心周りの相対運動」に分離させました。
結果は以下です(‘◇’)ゞ
「重心運動に依るハミルトニアン」量子力学的取り扱い
-\frac{\hbar^2}{2M}\nabla_{\boldsymbol{R}}^2\psi_{M}(\boldsymbol{R}) = E_{R}\psi_{M}(\boldsymbol{R}) \tag{14}
\end{align*}
「重心周りの相対運動のハミルトニアン」量子力学的取り扱い
\bigg(-\frac{\hbar^2}{2\mu}\nabla_{\boldsymbol{r}}^2+V(r)\bigg)\phi_{re}(\boldsymbol{r}) = E_{re}\phi_{re}(\boldsymbol{r}) \tag{15}
\end{align*}
比熱の期待値を求めるためには、(12)(13)式の偏微分方程式を解くしかないのですが、それは次回の記事で書くとしましょう(^^)/
お勧めの参考書
お勧めの参考書を紹介しておきます。
統計力学
今回は量子力学の知識も必要になってくるので、以下の参考書がとても分かりやすいです。
(今回の2原子分子の変数分離の話もあります)