こんにちは(@t_kun_kamakiri)(‘◇’)ゞ
本内容は、「比熱の温度依存性の理解のため」のための記事です。
シリーズ化していますので「なぜ比熱に温度依存性があるのか?」を知りたい方は、以下のシリーズを読んで頂ければ理解できると思います。
本記事を読むにあたって詳細の計算まで踏み込んで議論していては、時間がかかりすぎるため前提にしている知識が3つあります。
必要とする前提知識
- 古典力学
- 統計力学(平衡)
- じゃっかんの量子力学の知識
前回の記事の内容
前回の記事内容のまとめを書いておきます。
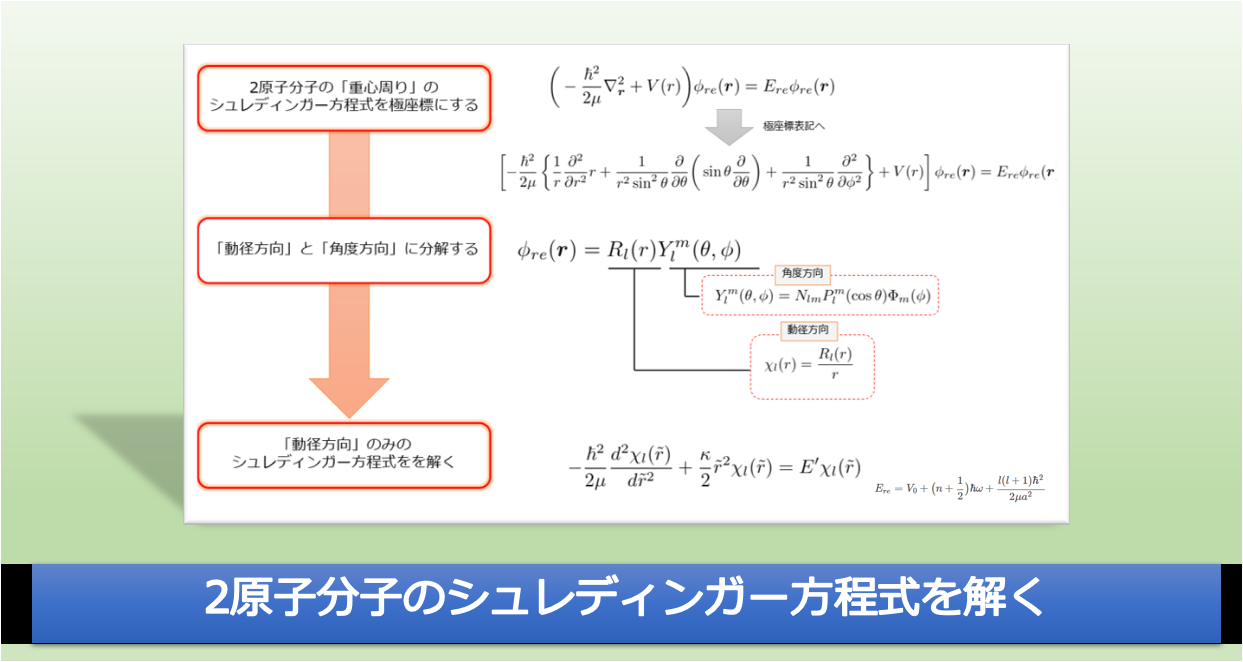
前回の記事では、古典近似から2原子分子の比熱を求めました!
求め方の流れは以下です。
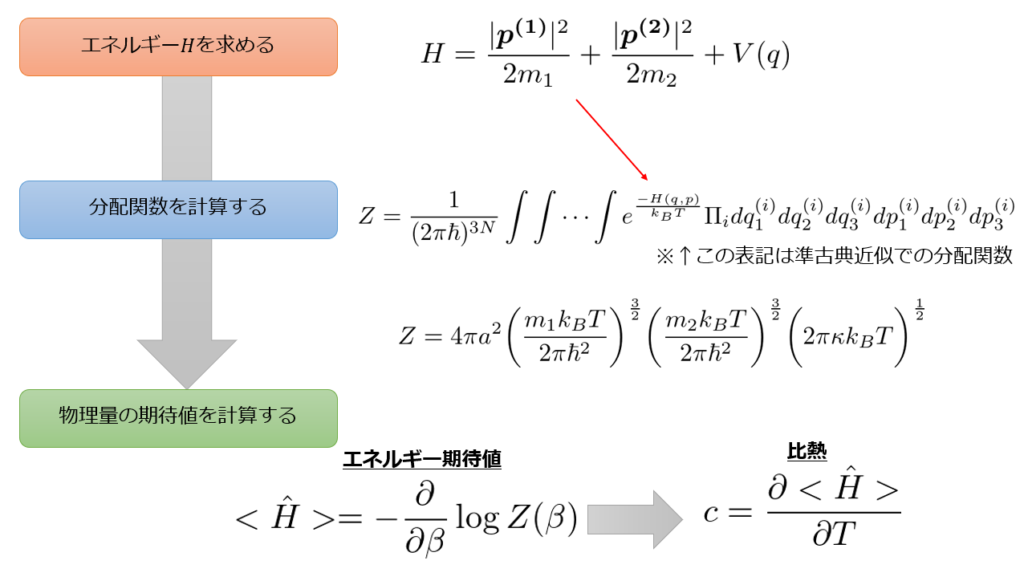
以上の流れで「古典近似における2原子分子の比熱」が計算でき、結果は・・・
古典近似における2原子分子の比熱
c=\frac{7}{2} k_B
\end{align*}
※実はこの「2原子分子の比熱」は実験値とは一致していません。
以下の2点が実験事実です。
- 2原子分子の比熱は\(\frac{5}{2}k_B \)に近い
- 比熱は温度の広い範囲で一定値であるが、温度依存性を持っている
この2点は「古典力学」の範疇では答えることができません。
「なぜ古典力学から理論的に求めた比熱」と「実験値の比熱」が異なるのか、また比熱になぜ温度依存性があるのかについては量子力学の知識が必要となるわけです(‘ω’)
本記事では比熱が運動の自由度から来ているということをもう少し探っていきます。
2原子分子のハミルトニアンを「重心運動」と「相対運動」に分ける
比熱が運動の自由度から来ているという意味をもう少し深く考えることにします。
例えば、単原子分子はひとつの原子として運動するため、並進運動しかありません。
(もちろん分子に大きさがあると考えると、原子核の回転エネルギーを考える必要があります。しかし、そのエネルギーはとても大きいためほとんんどの温度領域で基底状態にいるためエネルギーの自由度としてはカウントする必要がありません。)
2原子分子は、分子の並進運動だけでなく分子の空間的な運動(回転運動、振動運動)のような分子内部構造も熱力学的な性質(比熱など・・・)に影響を与えます。
今、2原子分子の原子間の相互作用(バネのような相互作用ポテンシャル)は考えますが、分子間の相互作用は無視できるもの(理想気体を想定)とします。
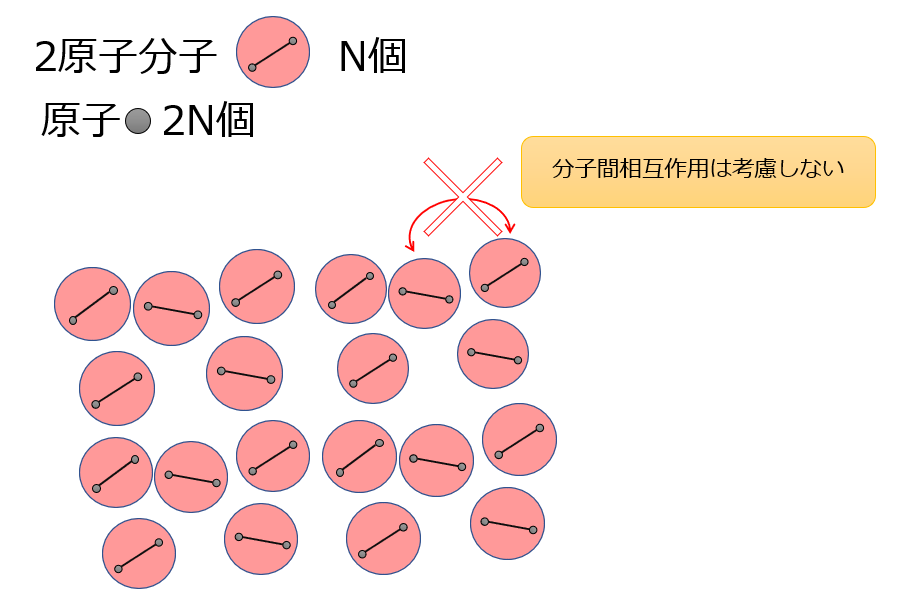

分子間力を考慮しないということは、各分子は独立に運動している者と考えることができるため、比熱についてはひとつの2原子分子を考えるだけで情報としては十分です。
(※ひとつの2原子分子から求めた比熱を\(N\)倍するだけで良いため)
分子の内部構造(内部自由度)を理解しやすくするために、
2原子分子をあたかも単原子分子の運動のように扱うために、2原子分子のハミルトニアン
H=\frac{|\boldsymbol{p^{(1)}}|^2}{2m_{1}}+\frac{|\boldsymbol{p^{(2)}}|^2}{2m_{2}}+V(q)\tag{1}
\end{align*}
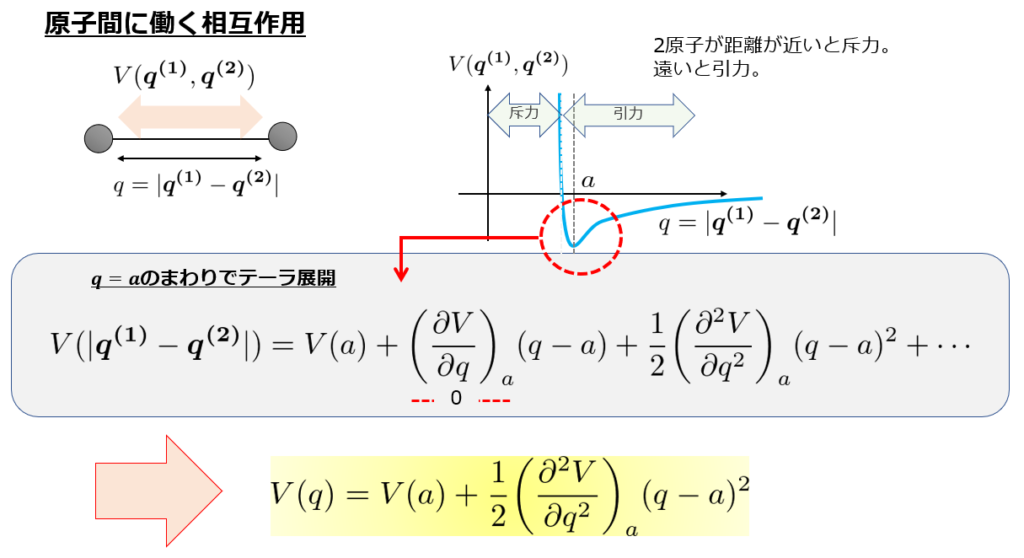

原子間の相互作用ポテンシャルについては、\(V(q)=\frac{\kappa}{2}(q-a)^2\)とします。
2原子分子の「重心運動」と「重心まわりの相対運動」に分解するとわかりやすくなります。
その分解する手続きを示しておきましょう。
まず絵のように2原子のベクトル(\(\boldsymbol{r_{1}},\boldsymbol{r_{2}}\))と、2原子の重心ベクトルを定義します。
- 重心の質量:\(M=m_1+m_2\)
- 重心のベクトル:\(\boldsymbol{r_{M}}=\frac{m_1\boldsymbol{r}_{1}+m_2\boldsymbol{r_{2}}}{m_1+m_2}\)
- 相対位置:\(\boldsymbol{r}=\boldsymbol{r_{1}}-\boldsymbol{r_{2}}\)
※\(q=r\) - 換算質量:\(\mu=\frac{m_1 m_2}{m_1+m_2}\)
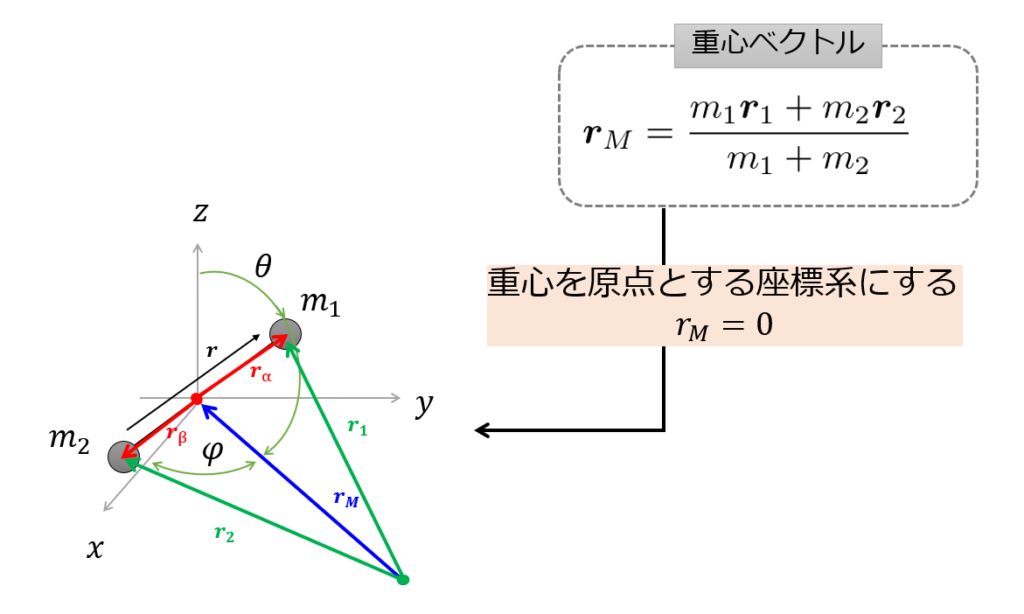

そうすると重心を基準にしたときの、各原子のベクトル(\(\boldsymbol{r_{\alpha}},\boldsymbol{r_{\beta}}\))が、
\(\boldsymbol{r_{\alpha}}=\frac{m_2}{M}\boldsymbol{r}\),\(\boldsymbol{r_{\beta}}=-\frac{m_1}{M}\boldsymbol{r}\)のように逆比で書くことができます。
2原子の運動エネルギーは、(1)式の2項までですが、位置の時間微分で書くと、
K &= \frac{m_1}{2}\dot{\boldsymbol{r_1}}^2+\frac{m_2}{2}\dot{\boldsymbol{r_2}}^2 \\
&= \frac{m_1}{2}\big(\dot{\boldsymbol{r_M}}^2+\dot{\boldsymbol{r_{\alpha}}}\big)^2+\frac{m_1}{2}\big(\dot{\boldsymbol{r_M}}+\dot{\boldsymbol{r_{\beta}}}\big)^2 \\
&=\frac{m_1+m_2}{2}\dot{\boldsymbol{r_M}}+m_1\dot{\boldsymbol{r_M}}\dot{\boldsymbol{r_{\alpha}}}+m_2\dot{\boldsymbol{r_M}}\dot{\boldsymbol{r_{\beta}}} +\frac{m_{1}}{2}\dot{\boldsymbol{r_{\alpha}}}^2+\frac{m_{2}}{2}\dot{\boldsymbol{r_{\beta}}}^2 \\
&= \frac{M}{2}\dot{\boldsymbol{r_M}}^2+\frac{\mu}{2}\dot{\boldsymbol{r}}^2\tag{2}
\end{align*}
です。
回転運動は極座標表示で考えよう
2原子分子の場合は、単原子分子の場合と違って回転運動など(内部構造による運動)が入りますという話をしました。
回転によるエネルギーとは何かというと、
です。
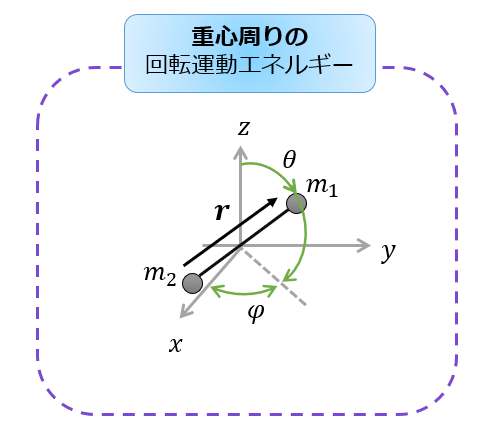
今回は、重心周りで2原子が回転しているを考えることにします。
※2原子間の距離が変わると質量の異なる2つの原子においては重心位置が変わるため計算が複雑になります。
今回考えるのは回転運動をだけなので、回転運動には極座標表示で考える方が扱いやすいですよね。
\boldsymbol{r}=\big(r\sin\theta\cos\phi,r \sin\theta\sin\phi,r \cos\theta\big)
\end{align*}

\left\{\begin{matrix}
x &=&r\sin\theta\cos\phi\\
y&=& r \sin\theta\sin\phi\\
z &=&r \cos\theta\\
\end{matrix}\right.\tag{3}
\end{align*}
これを時間微分します。
\left\{\begin{matrix}
\dot{x} &=& \dot{r} \sin\theta\cos\phi+r \cos\theta\cos\phi\dot{\theta}-r\sin\theta\cos\phi\dot{\phi}\\
\dot{y}&=&\dot{r} \sin\theta\sin\phi+ r \cos\theta\sin\phi\dot{\theta}+r\sin\theta\sin\phi\dot{\phi}\\
\dot{z} &=&\dot{r}\cos\theta-r\sin\theta\dot{\theta}\\
\end{matrix}\right.\tag{4}
\end{align*}
極座標表示が完成しました。
では、(4)式を用いると・・・
2原子の重心周りの相対運動エネルギー
\frac{\mu}{2}\boldsymbol{r}^2 &=\frac{\mu}{2}\big(\dot{r}^2+r^2\dot{\theta}^2+r^2\sin^2\theta \dot{\phi}^2\big)\\
&=\frac{\mu\dot{r}^2}{2}+\frac{I}{2}\big(\dot{\theta}^2+\sin^2\theta \dot{\phi}^2\big)\tag{5}
\end{align*}
※\(I=\mu r^2\)慣性モーメント
これは「位置」と「位置の時間微分(速度に値する量)」で記述された運動エネルギーですが、分配関数を求めるには「位置」と「運動量」で書かれた相空間で積分する必要があります。
そこで、変数が「位置」と「運動量」を持つようなハミルトニアンを求めることにします。
これには、「位置の時間微分(一般速度)」を「運動量」に変える必要がありますよね。
その方法はこちらです。
それにより、一般座標\(q\)とそれに共役な一般運動量\(p\)からなハミルトニアン\(H(q,p)\)を計算することができます。
なので、まずは一般運動量を求めましょう。
(一般座標、一般運動量)の組み合わせを、
- (\(r,p_r\))
- (\(\theta,p_{\theta}\))
- (\(\phi,p_{\phi}\))
と書くことにすると、
\left\{\begin{matrix}
\boldsymbol{p_{M}} &= & \frac{\partial L}{\partial {\boldsymbol{\dot{r}_{M}}}} &=&M\boldsymbol{\dot{r}_{M}}\\
p_r& = & \frac{\partial L}{\partial \dot{r}}&=&\mu\dot{r}\\
p_{\theta} & = & \frac{\partial L}{\partial \dot{\theta}}&=&I\dot{\theta}\\
p_{\phi} & = & \frac{\partial L}{\partial \dot{\phi}}&=&I\sin^2\theta\dot{\phi}
\end{matrix}\right.
\end{align*}
これらを使うとハミルトニアンは、
H &=\boldsymbol{p_{M}}\cdot \boldsymbol{r_{M}}+p_{r}\dot{r}+p_{\theta}\dot{\theta}+p_{\phi}\dot{\phi}+\frac{\kappa^2}{2}(r-a)^2\\
&=\frac{\boldsymbol{p_{M}}^2}{2M}+\frac{1}{2I}\bigg(p_{\theta}^2+\frac{p_{\phi}^2}{\sin^2\theta}\bigg)+\frac{p_{r}^2}{2\mu}+\frac{\kappa^2}{2}(r-a)^2\tag{6}
\end{align*}


これでハミルトニアンを「重心運動」と「相対運動」に分けることができたので、比熱を求めるために分配関数を求めてみます!
分配関数を求める
ハミルトニアンがわかったら比熱を求める手順はいつも同じです。



今回の場合、ハミルトニアンから分配関数を求める計算手続きは以下となります。


分配関数を計算する際の注意点としては、積分する\(d\boldsymbol{r}d\boldsymbol{p}\)においては、位置座標に対して共役な運動量を使う必要があります。
例えば、重心の並進運動エネルギーから来る分配関数\(Z_{G}\)の積分\(d\boldsymbol{R}d\boldsymbol{p}\)としていますが、これは直交座標系に対する積分を行います。
しかし、その他の相対運動エネルギーから来る分配関数\(Z_{rot}\)と\(Z_{vib}\)の積分\(d\boldsymbol{r}d\boldsymbol{p}_{re}\)は、極座標系に対する積分を行います。
ここで、わかりやすくするために以下のように分解しました。
重心の並進運動エネルギーからの分配関数
Z_{G} &=\frac{1}{(2\pi\hbar)^{3}}\int\int \exp\bigg(-\frac{1}{k_B T}\frac{\boldsymbol{p}^2}{2M}\bigg)d\boldsymbol{p}d\boldsymbol{R}\\
&=\frac{1}{(2\pi\hbar)^{3}}\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}\int^{\infty}_{-\infty} \exp\bigg(-\frac{1}{k_B T}\frac{p_{x}^2+p_{y}^2+p_{z}^2}{2M}\bigg)\,dp_{x}\,dp_{y}\,dp_{z}\,dR_{x}\,dR_{y}\,dR_{z}\\
&=\frac{1}{(2\pi\hbar)^{3}}\big(2\pi Mk_B T\big)^{\frac{3}{2}}\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}\,dR_{x}\,dR_{y}\,dR_{z}\\
&=\frac{1}{(2\pi\hbar)^{3}}\big(2\pi Mk_B T\big)^{\frac{3}{2}}V\\
&=A\big(k_B T\big)^{\frac{3}{2}}\tag{7}
\end{align*}
2原子間の相対位置変化による振動運動エネルギーからの分配関数
Z_{rot} &=\frac{1}{(2\pi\hbar)^{2}}\int^{2\pi}_{0}\int^{\pi}_{0}\int^{\infty}_{-\infty}\int^{\infty}_{-\infty} \exp\bigg[-\frac{1}{k_B T}\frac{1}{2I}\bigg(p_{\theta}^2+\frac{p_{\phi}^2}{\sin^2\theta}\bigg)\bigg] d\theta\, dp_{\theta}\, d\phi\,dp_{\phi}\\
&=\frac{1}{(2\pi\hbar)^{2}}\int^{2\pi}_{0}\int^{\pi}_{0}\sqrt{2\pi Ik_{B}T}\sqrt{2\pi Ik_{B}T\sin^2\theta}\, d\theta\, d\phi\\
&=\frac{2Ik_{B}T}{\hbar^2}\\
&=B\big(k_B T\big)^{\frac{2}{2}}\tag{8}
\end{align*}
重心周りの回転運動エネルギーからの分配関数
Z_{vib} &=\frac{1}{(2\pi\hbar)^{1}}\int^{\infty}_{-\infty}\int^{\infty}_{-\infty} \exp\bigg[-\frac{1}{k_B T}\bigg(\frac{p_{r}^2}{2\mu}+\frac{\kappa}{2}(r-a)^2\bigg)\bigg]\,dr\,dp_{r}\\
&=\frac{1}{(2\pi\hbar)^{1}}\sqrt{2\pi \mu k_{B}T}\sqrt{\frac{2\pi k_{B}T}{\kappa}}\\
&=C\big(k_B T\big)^{\frac{2}{2}}\tag{10}
\end{align*}
となります。
特にきれいにまとめることはしなかったですが、とても重要なのは\(k_{B}T\)が何乗になっているかです。
あえて\(\big(k_B T\big)^{\frac{f}{2}}\)の形にしたのは、自由度\(f\)がわかりやすいからです。
(8)(9)(10)式の計算方法は、下記の記事を参考にして下さい。
エネルギーの期待値を求める
比熱はエネルギーを温度で微分した物理量であるため、まずはエネルギーの期待値を求めましょう。
エネルギーの期待値
<\hat{H}>=-\frac{\partial }{\partial \beta}\log Z(\beta)=-\frac{\partial }{\partial \beta}\bigg(\log Z_{G}(\beta)+\log Z_{rot}(\beta)+\log Z_{vib}(\beta)\bigg)\tag{11}
\end{align*}
これを見ると、分配関数が各運動エネルギーの項で分解されているのがわかります。
分配関数の係数部分は\(D\)とおいてまとめて、計算しやすいように\(\beta=\frac{1}{k_B T}\)と置いておきます。
Z &=Z_{G}Z_{rot}Z_{vib}\\
&=A\big(k_B T\big)^{\frac{3}{2}}\times B\big(k_B T\big)^{\frac{2}{2}}\times C\big(k_B T\big)^{\frac{2}{2}}\\
&=D\big(k_B T\big)^{\frac{7}{2}}\\
&=D\beta^{-\frac{7}{2}}
\end{align*}
これを(7)式に代入すると、
<\hat{H}>=-\frac{\partial }{\partial \beta}\bigg(\log D+ \log \beta^{-\frac{7}{2}}\bigg)=\frac{7}{2}k_B T
\end{align*}
となります。
比熱を求める
よって、比熱\(c=\frac{\partial }{\partial T}<\hat{H}>\)は、
c=\frac{7}{2} k_B\tag{12}
\end{align*}
となります。
まとめ
2原子分子の運動に関して、「重心運動」「2原子間の振動運動」「重心周りの回転運動」に分解し分配関数を計算しました。
| エネルギー | 自由度 | |
| 重心運動 | 重心の並進運動エネルギー \(\frac{\boldsymbol{p_{M}}^2}{2M}\) |
3 |
| 2原子間の振動運動 | 運動エネルギー+振動エネルギー \(\frac{p_{r}^2}{2\mu}+\frac{\kappa^2}{2}r^2\) |
2 |
| 重心周りに回転運動 | 回転運動エネルギー \(\frac{1}{2I}\bigg(p_{\theta}^2+\frac{p_{\phi}^2}{\sin^2\theta}\bigg)\) |
2 |
自由度は「位置」or「運動量」の2乗の項が何個あるのかで決まっていましたよね。
補足
比熱に関しては、「位置の2乗」や「運動量の2乗」の項がいくつかるかによって比熱の大きさが決まってくるという話を前回の記事でしました。
まとめると以下です。
- 運動エネルギーは運動量の2次関数であり、自由度\(f\)とすれば、
\begin{align*}K=\sum_{i=1}^{f}\alpha_{i}^2p_{i}^2\end{align*}
と表される場合、分配関数\(Z\)の温度は\(\frac{f}{2}\)乗となり、比熱は\(\frac{f}{2}k_B\)となる。
また、
- 相互作用ポテンシャルエネルギーが位置の2次関数であり、自由度\(f\)とすれば、
\begin{align*}K=\sum_{i=1}^{f}\alpha_{i}^2r_{i}^2\end{align*}
と表される場合、分配関数\(Z\)の温度は\(\frac{f}{2}\)乗となり、比熱は\(\frac{f}{2}k_B\)となる。