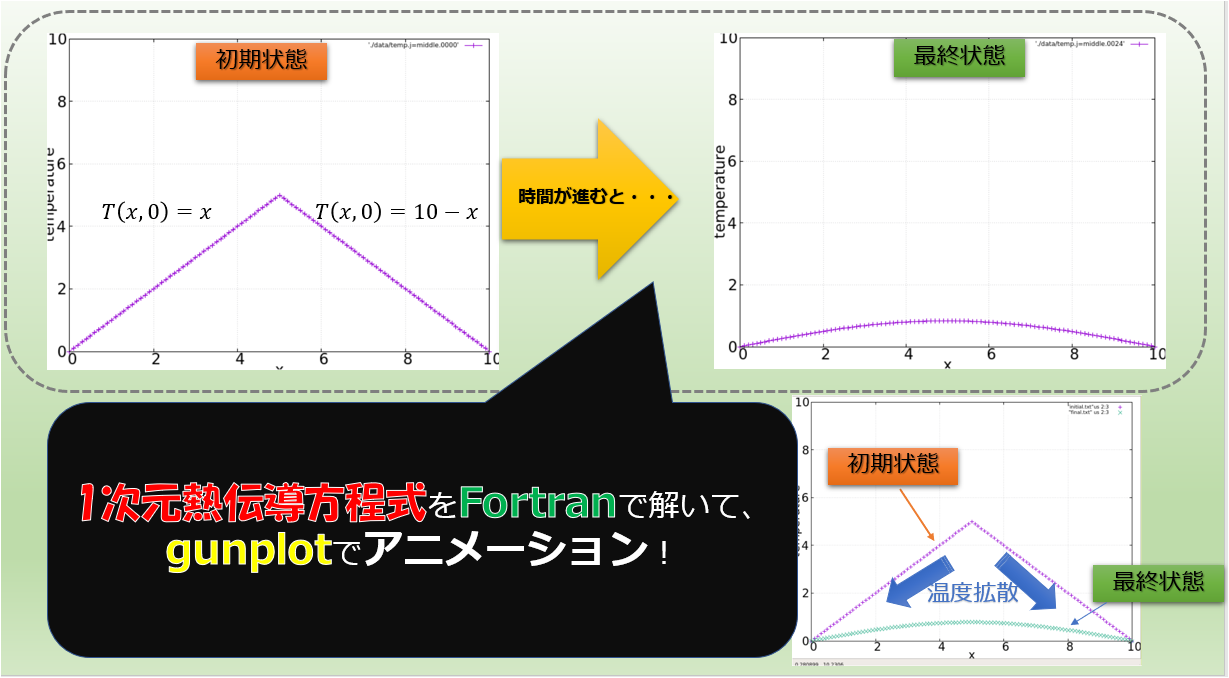
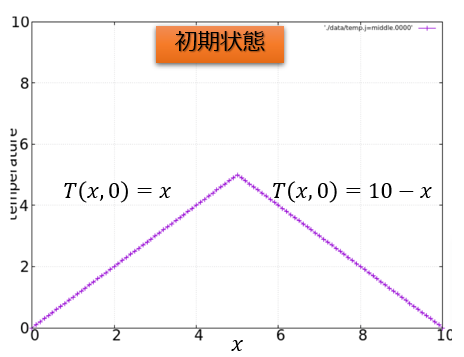
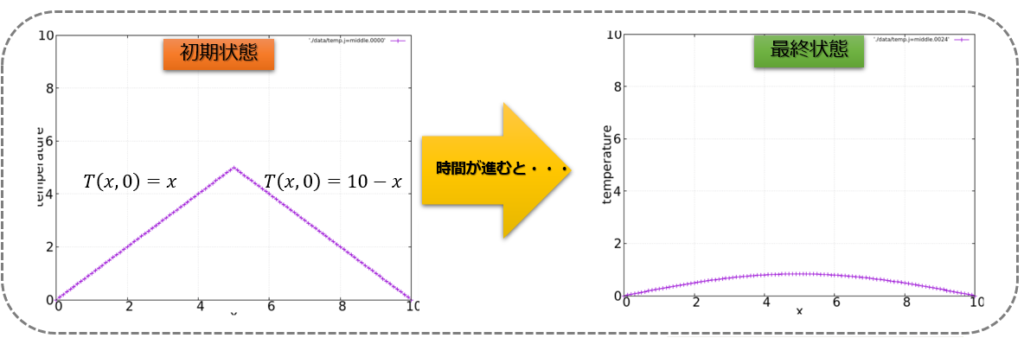
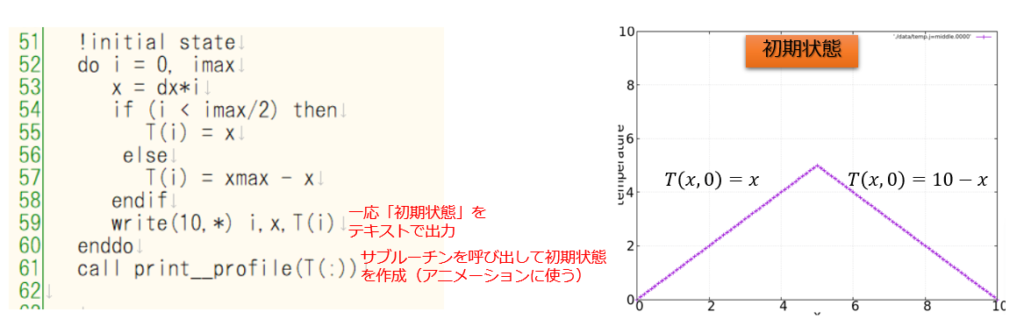
こんにちは(@t_kun_kamakiri)(‘◇’)ゞ
Fortranを学生時代に使っていたのですが、最近になって使い始めています。
完全に趣味です(^^)/
それはそうと、Fortranは数値計算する上では直感的でとてもわかりやすい言語だと個人的には思っているのですが、めんどくさい点があるのです。
それは、Fortranってグラフ作成などの可視化ツールがない・・・・(_;
他のプログラミング言語に詳しくないから何とも言えないですが、Pythonとか対話型のプログラミング言語なら可視化のライブラリが用意されているのに・・・
Fortranでよく使うグラフ作成ツールと言えば、gnuplot(ニュープロット)かなと思っています。
1次元グラフをどうやってgnuplotでアニメーションするのか?
※FortranのコードはFortran90/95の書き方にしているつもりですが正確に書けているかは不明です。
※FortranはWSLを使ってインストールしています。
※gnuplotはこのサイトを参考にすれば良いかと思います。
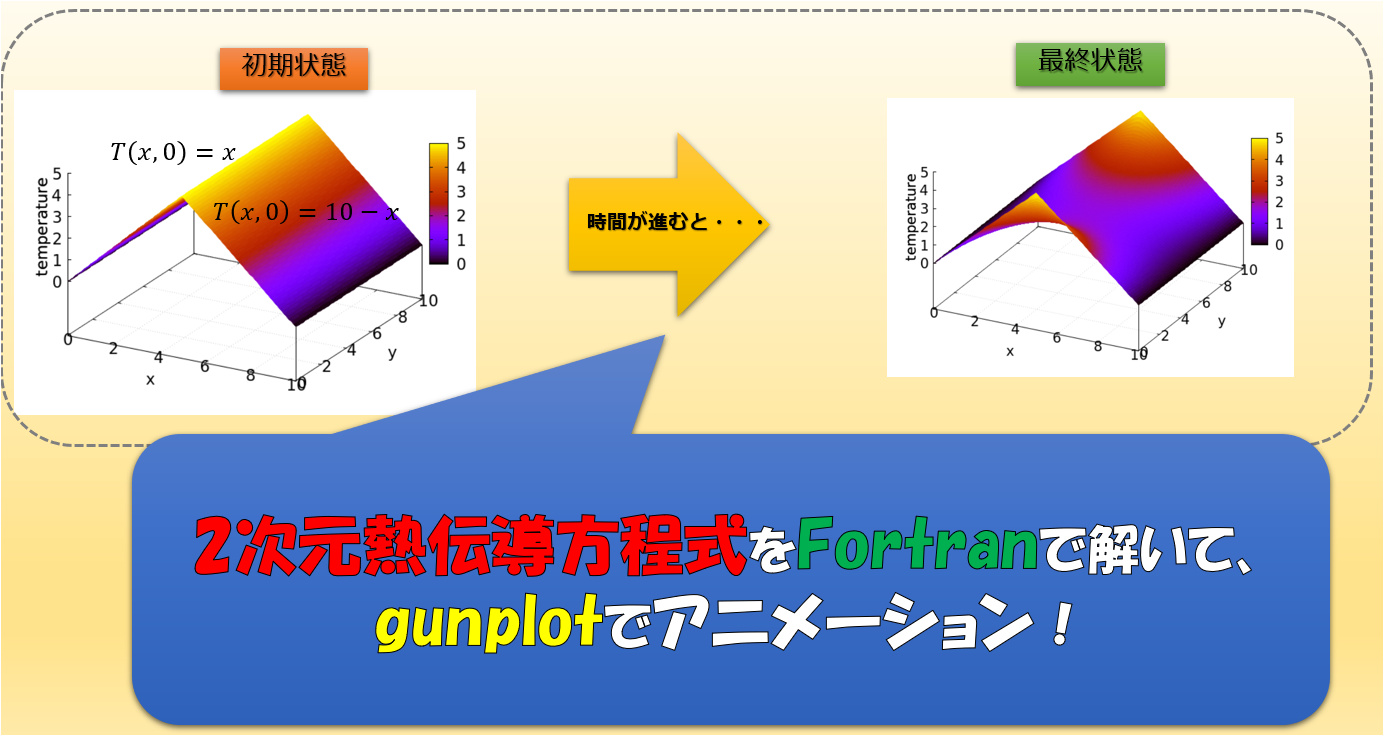
1次元熱伝導方程式をFortranで解く
まずは解くべき方程式を明らかにしておきましょう。
全体の流れ
アニメーション作成までの全体の流れを押さえておくと少し気持ちのハードルは下がるかもしれないので、先に全体の流れを示しておきます。


- 1次元熱伝達方程式は偏微分方程式であるため、それを数値的に解くためには離散化してあげる必要があります。
今回は、「時間に対しては陽解法」「空間に対しては2次精度」で解くことを考えています。 - 次にForranを使って離散化した方程式を数値的に解くことを考えます。
(※コードは後ほど) - Fortranで出力したデータをgnuplotで順番に読み込んでいくためのスクリプトをFortranを使って作成します。
これらのことができれば、あとはgnuplotで「3.」で作成されたスクリプトを実行するだけアニメーションを作成することができます。
※1次元熱伝導方程式を題材にしたのは、簡単な方程式の方がアニメーション作成の方法を理解しやすいと思ったからです。
ゆえに、離散化も特にこだわってはいません。
1次元熱伝導方程式の離散化
- 時間微分の項(左辺)
- 空間微分の項(右辺)
をどのように扱うのかが問題です。
いっちばん手っ取り早い離散化で進めていきましょう。
ある地点(x_{i})での時間微分の項
Fortranで解く
Fortranで解くと言ってもプログラムを書かないことには何も始まらないので、プログラムを書きます。
以下がプログラムです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 |
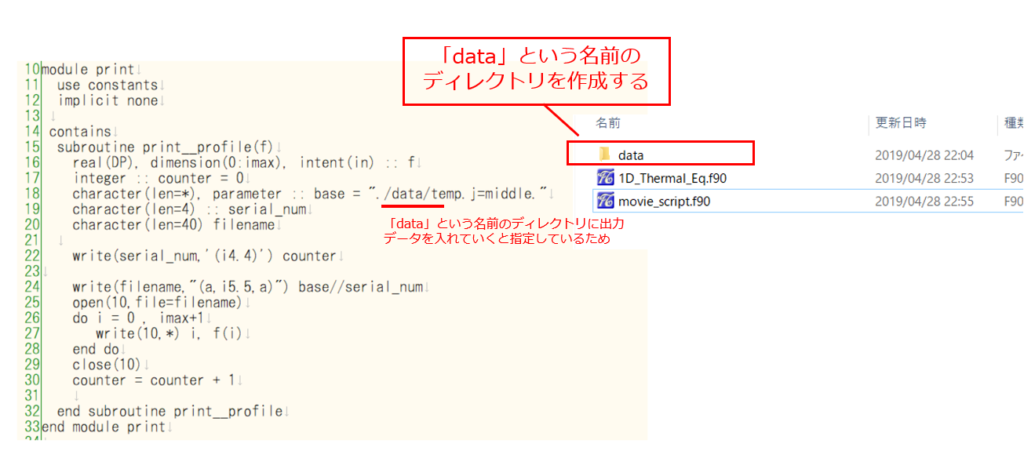
!ファイル名 1D_Thermal_Eq.f90 module constants implicit none integer::i,nt integer, parameter :: imax = 100,ntmax = 2500 real(8):: T(0:imax),xmax,x,dx,dt,kp integer,parameter :: SP = kind(1.0) integer,parameter :: DP = selected_real_kind(2*precision(1.0_SP)) end module constants module print use constants implicit none contains subroutine print__profile(f) real(DP), dimension(0:imax), intent(in) :: f integer :: counter = 0 character(len=*), parameter :: base = "./data/temp.j=middle." character(len=4) :: serial_num character(len=40) filename write(serial_num,'(i4.4)') counter write(filename,"(a,i5.5,a)") base//serial_num open(10,file=filename) do i = 0 , imax write(10,*) i*dx, f(i) end do close(10) counter = counter + 1 end subroutine print__profile end module print program thermal_explicit use constants use print implicit none dt = 0.004 kp = 1 xmax = 10 dx = xmax/imax open(10,file="initial.txt") open(11,file="final.txt") !initial state do i = 0, imax x = dx*i if (i < imax/2) then T(i) = x else T(i) = xmax - x endif write(10,*) i,x,T(i) enddo call print__profile(T(:)) !Time step do nt = 1, ntmax do i = 1, imax-1 T(i) = T(i) + kp*dt/(dx*dx)*(T(i+1)- 2*T(i) +T(i-1)) end do if (mod(nt,100)==0) call print__profile(T(:)) write(*,*)nt end do !Final state do i = 0, imax x = dx*i write(11,*) i,x,T(i) end do end program thermal_explicit |
プログラムだけ載せられてもよくわからんという人もいるかもしれないので、説明を加えておきます(‘ω’)


|
1 2 |
gfortran 1D_Thermal_Eq.f90 ./a.out |
実行ができれば「data」という名前のディレクトリの中に、以下のように大量のデータが保存されていることが確認できます。
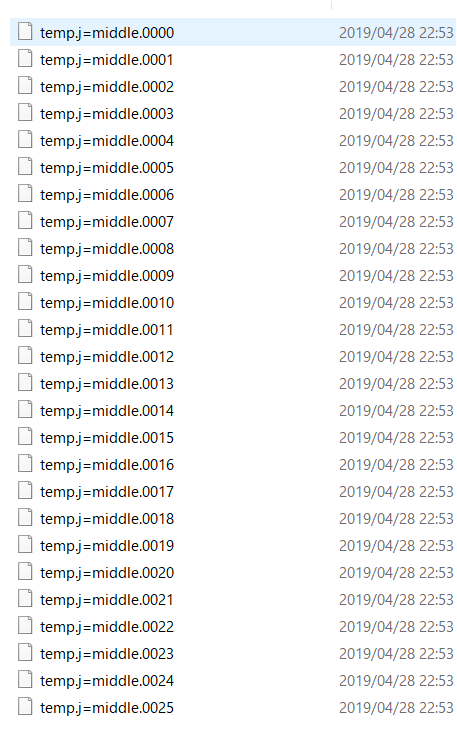

これらのデータが指定したタイムステップで出力された温度の空間分布のデータです。
あとは、これらのデータを順番にgnuplotで読み込めばアニメーションが完成ということになります。
そのためには、gnuplotのスクリプトが必要になります。
スクリプトは書くのが少々面倒なので、スクリプト自体をFortranで書くことにします。
アニメーション用のgnuplotのスクリプトをFortranで作成
gnuplotのスクリプトを作成するためのFortranのプログラムがこちらです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
program animation_script implicit none integer, parameter :: imax = 100,xmax = 10 integer :: counter, counter_end = 24,dx character(len=*), parameter :: base='./data/temp.j=middle.' character(len=4) :: serial_num dx = xmax/imax print *, "#" print *, "# gnuplot script generated by movie_script.f90" print *, "#" print *, " " print *, "set xlabel 'x' # x-axis" print *, "set ylabel 'temperature' # y-axis" print *, "set xrange[0:", xmax, "] # j-grid min & max" print *, "set yrange[0.0:10.0] # temperature min & max" print *, "set grid" print *, "set xlabel font 'Arial,20' " print *, "set ylabel font 'Arial,20' " print *, "set tics font 'Arial,20'" do counter = 0 , counter_end write(serial_num,'(i4.4)') counter print *, "plot '"//base//serial_num//"' w lp" if ( counter==0) then print *, "pause 2" else print *, "pause 1" end if end do print *, "pause -1" end program animation_script |
これはあまり説明を必要としないのですが、簡単に説明すると「do文」のところで先ほどの「data」という名前のディレクトリ内の大量のデータを順番に読み込む作業を行っています。
|
1 2 |
gfortran movie_script.f90 ./a.out >movie |
「./a.out >movie」とするとmovieというファイルが出来上がり、その中にFortranの「print文」の内容を全て書き出してくれます。
この「movie」というファイルがgnuplotのスクリプトとなります。
以上のことが終えれば、あとはgnuplotで「movie」という名前のスクリプトを走らせるだけです。
アニメーションを作成してみよう(^^)/
「movie」というスクリプトは2通りの方法で実行できます。
方法1

↑このようにコマンドを打っても良いですし、
方法2


↑このように「gnuplot」と打って、「load “movie”」とスクリプトファイルをloadしても良いです。
アニメーションはこんな感じ
まとめ
はじめての人にもできるように、わかりやすくまとめてみました(‘◇’)ゞ
が、説明がくどく長い記事になってしまったことをお許しください(‘ω’)
まだまだFortranもgnuplotも勉強不足ですが、何とかできたかなっていう感じです。
ごちゃごちゃ説明してしまいましたが、下記のzipファイルを解凍して下記のコマンドを打ってお試しください。
|
1 2 3 4 5 |
gfortran 1D_Thermal_Eq.f90 ./a.out gfortran movie_script.f90 ./a.out >movie gnuplot movie |