こんにちは(@t_kun_kamakiri)。
先日の下記の勉強会で発表者の方が・・・・
(2019/7/27PM)第73回オープンCAE勉強会@関西+ビアガーデン交流会
と言った質問をされていました。
となりました(笑)
上記の記事でも書きましたが、覚えているもの(よく使うもの)を書き出しても、以下の3つくらいです・・・
代表的な1階微分の差分法
前進差分
後退差分
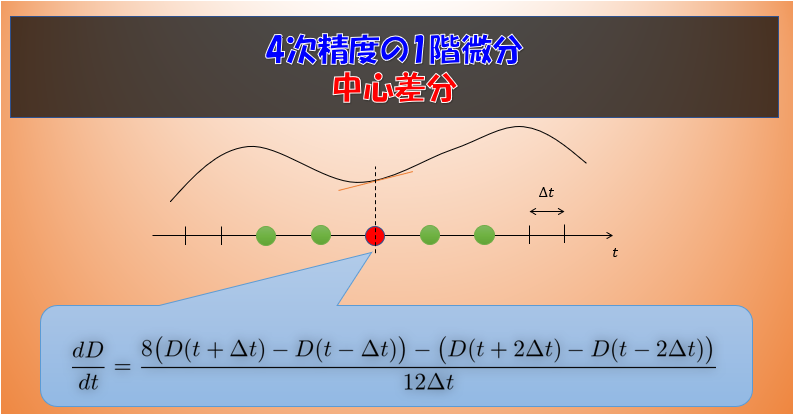
中心差分
そこで、思い出した!!
4次精度の中心差分なら導出したことがあるし、利用しているのも見たことがあるぞ!!
ということで、本記事の内容は、
4次の中心差分の結果
先に4次の中心差分の結果を書き下しておきます。
\frac{dD}{dt}=\frac{8\big(D(t+\Delta t)-D(t-\Delta t)\big)-\big(D(t+2\Delta t)-D(t-2\Delta t)\big)}{12\Delta t}
\end{align*}
はい、これです。
使用例はあるのか?
ひとつだけ例を見つけました(‘ω’)
tb-021-data-acquisition-and-injury-calculation-v20


これは、
VCがViscous Criterionの頭文字をとったもので、胸の傷害レベルを表現する量を意味しています。
胸の内部の粘性を表現している量ですが、ここで\(D\)が胸の変位量に対して、\(V\)が胸の変位量を1階微分した量です。
この時に、\(V(t)=\frac{dD}{dt}\)を計算する必要があり、1階微分を4次精度の中心差分で表現しています。
1階微分の4次精度の差分
\frac{dD}{dt}=\frac{8\big(D(t+\Delta t)-D(t-\Delta t)\big)-\big(D(t+2\Delta t)-D(t-2\Delta t)\big)}{12\Delta t}
\end{align*}
なぜ、1階微分を求めるのに前進差分や中心差分を使わずに、一見すると謎の差分法を使っているのかはわかりませんが、
これが本記事の内容の4次精度の中心差分を表現した形です。
1階微分の4次の中心差分を導出してみる
前進差分も後退差分の場合も、
精度として保証できそうな次数までテーラー展開をしてすることで求めることができます。
今回は、4次の項までテーラー展開を行い、
出てきた以下の(1)式~(4)式を式変形することで、1階微分を差分で表現します。
D(t+\Delta t)&=D(t)+\frac{dD}{dt}\Delta t+\frac{1}{2}\frac{d^2D}{dt^2}\big(\Delta t\big)^2\\
&+\frac{1}{6}\frac{d^3D}{dt^3}\big(\Delta t\big)^3+\frac{1}{24}\frac{d^4D}{dt^4}\big(\Delta t\big)^4+\mathcal{O}(\Delta t^5)\tag{1}
\end{align*}
D(t-\Delta t)&=D(t)-\frac{dD}{dt}\Delta t+\frac{1}{2}\frac{d^2D}{dt^2}\big(\Delta t\big)^2\\
&-\frac{1}{6}\frac{d^3D}{dt^3}\big(\Delta t\big)^3+\frac{1}{24}\frac{d^4D}{dt^4}\big(\Delta t\big)^4+\mathcal{O}(\Delta t^5)\tag{2}
\end{align*}
D(t+2\Delta t)&=D(t)+\frac{dD}{dt}\big(2\Delta t)+\frac{1}{2}\frac{d^2D}{dt^2}\big(2\Delta t\big)^2\\
&+\frac{1}{6}\frac{d^3D}{dt^3}\big(2\Delta t\big)^3+\frac{1}{24}\frac{d^4D}{dt^4}\big(2\Delta t\big)^4+\mathcal{O}(\Delta t^5)\tag{3}
\end{align*}
D(t-2\Delta t)&=D(t)-\frac{dD}{dt}\big(2\Delta t\big)+\frac{1}{2}\frac{d^2D}{dt^2}\big(2\Delta t\big)^2\\
&-\frac{1}{6}\frac{d^3D}{dt^3}\big(2\Delta t\big)^3+\frac{1}{24}\frac{2d^4D}{dt^4}\big(2\Delta t\big)^4+\mathcal{O}(\Delta t^5)\tag{4}
\end{align*}
以上で、4次の項までテーラー展開をした結果が用意できました。
ここから・・・
(1)-(2)をすると、
D(t+\Delta t)-D(t-\Delta t)=2\frac{dD}{dt}\Delta t+\frac{1}{3}\frac{d^3D}{dt^3}\big(\Delta t\big)^3\tag{5}
\end{align*}
(3)-(4)をすると、
D(t+2\Delta t)-D(t-2\Delta t)=4\frac{dD}{dt}\Delta t+\frac{8}{3}\frac{d^3D}{dt^3}\big(\Delta t\big)^3\tag{6}
\end{align*}
さらに、(5)×8-(6)をすることで1階微分の4次精度の差分が完成します。
\frac{dD}{dt}=\frac{8\big(D(t+\Delta t)-D(t-\Delta t)\big)-\big(D(t+2\Delta t)-D(t-2\Delta t)\big)}{12\Delta t}\tag{7}
\end{align*}
2つとなりの点まで利用して、1階微分を表現しているのがわかります。
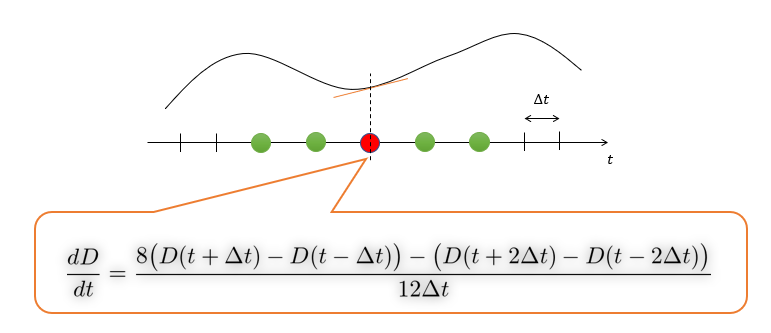

ということで、興味のある方は6次精度、10次精度・・・n次精度など試してください!
差分の違いで数値計算の結果が変わってくるので差分の選択は慎重に!
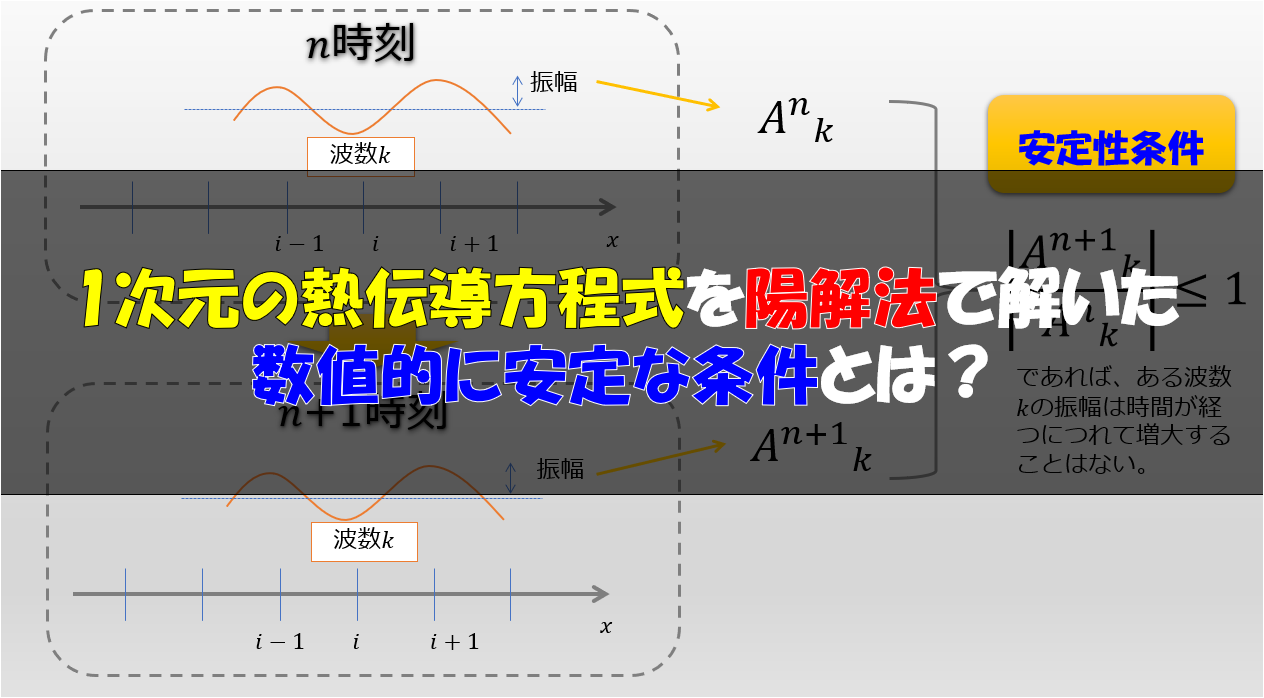
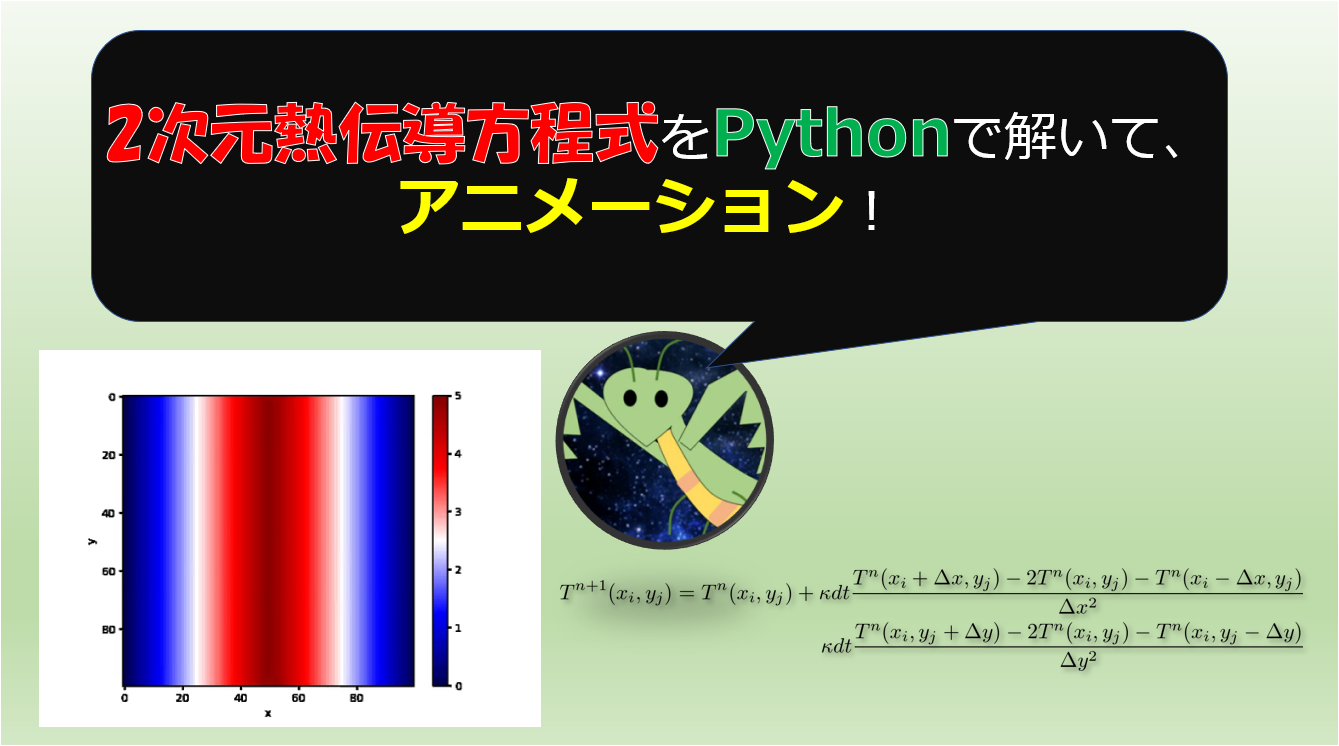
4次の中心差分についての記事ではないですが、以前に「前進差分、後退差分、中心差分」で移流方程式を数値計算でシミュレーションしてみました。
テーラー展開の次数をとにかく上げれば、良い結果が得られるというわけではなく、方程式の解の安定性なども考慮して計算する必要があるという良い例ですので、良ければ上記の記事もどうぞ(^^)/














[…] 【1階微分!中心差分の4次精度】テーラー展開から真面目に導出してみた。 […]