【2次精度の片側差分】 1階微分と2階微分を離散化する。

当ブログを読んでくれた方から質問をもらったので、記事にして回答したいと思います。

基本的に質問に対しては、お答えするスタンスです(‘◇’)ゞ

☟頂いた質問内容はこちら・・・

👆こんな感じの質問です。

カマキリ

どの記事を読んだ際の質問か？

記事はこちら

【1階微分！中心差分の4次精度】テーラー展開から真面目に導出してみた。

カマキリ

質問内容は？

「乱流の数値シミュレーション」のp.28(2.24)、(2.25)の導出方法がわからないから教えてほしいという内容です。
ちなみに「乱流の数値シミュレーション」とは☟こちらの書籍です。

乱流の数値シミュレーション改訂版

梶島岳夫

4,975円(04/15 21:30時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

こちらの書籍は乱流モデルについて、標準的な難易度でわかりやすく書かれています(‘ω’)
宣伝はさておき・・・・

本日の記事の内容はこちら☟

記事の内容はこちら

「乱流の数値シミュレーション」

p.28(2.24)、(2.25)
p.29(2.28)、(2.29)

を導出する。

p.28(2.24)、(2.25)は何かというと・・・・☟これです。

\(\frac{df}{dx}\)のような一階微分を、等間隔格子での片側差分でどう表されるのかという話です。
結果を示しておくと・・・

(2.24)

\begin{align*}
f^{\prime}=\frac{f_{j-2}-4f_{j-1}+3f_{j}}{2\Delta}+\frac{\Delta^2}{3}f^{(3)}_{j}+\omicron[\Delta^3]\tag{2.24}
\end{align*}

(2.25)

\begin{align*}
f^{\prime}=\frac{-3f_{j}+4f_{j+1}-f_{j+2}}{2\Delta}-\frac{\Delta^2}{3}f^{(3)}_{j}+\omicron[\Delta^3]\tag{2.25}
\end{align*}

\(f^{(3)}_{j}\)は\(\frac{d^3 f}{dx^3}\)の意味ですが、数値計算ではこの項は使わないので(2.24)(2.25)はテーラー展開の2次の項までしか使っていないため、2次精度の離散化です。

※ここでの\(\Delta\)は、\(\Delta x\)の意味です。

※余談ですが、片側差分だと下記のような「前進差分」や「後退差分」があります。

前進差分

\begin{align*}\frac{df}{dx}=\frac{f(x+\Delta x)-f(x)}{\Delta x}\end{align*}

後退差分

\begin{align*}\frac{df}{dx}=\frac{f(x)-f(x-\Delta x)}{\Delta x}\end{align*}

質問内容から、p.29の(2.28),(2.29)の導出方法もわからないと思うので、合わせて解説をしたいと思います。

p.29(2.28)、(2.29)は何かというと・・・・☟これです。

ちなみに、p.29の(2.28),(2.29)は\(\frac{d^2 f}{dx^2}\)のような二階微分を、等間隔格子での片側差分でどう表されるのかという話です。
結果を示しておくと・・・

(2.28)

\begin{align*}
f^{\prime\prime}=\frac{-f_{j-3}+4f_{j-2}-5f_{j-1}+2f_{j}}{\Delta^2}+\frac{11\Delta^2}{12}f^{(4)}_{j}+\omicron[\Delta^3]\tag{2.28}
\end{align*}

(2.29)

\begin{align*}
f^{\prime\prime}=\frac{2f_{j}-5f_{j+1}+4f_{j+2}-f_{j+3}}{\Delta^2}+\frac{11\Delta^2}{12}f^{(4)}_{j}+\omicron[\Delta^3]\tag{2.29}
\end{align*}

\(f^{(4)}_{j}\)は\(\frac{d^4 f}{dx^4}\)の意味ですが、数値計算ではこの項は使わないので(2.28)(2.29)はテーラー展開の2次の項までしか使っていないため、2次精度の離散化です。

※ここでの\(\Delta\)は、\(\Delta x\)の意味です。

早速、導出をしていこうと思いますが、(2.24)(2.25)は基本的に同じ導出の仕方なので(2.24)のみ導出します。
また、(2.28)、(2.29)も同じ導出方法なので(2.28)のみ示します。

(2.24)(2.25)(2.28)(2.29)は全て同じ要領で導出できるのですが、それぞれ違う方法で導出してみます。

(2.24)(2.25)→連立方程式を代数的に解く
(2.28)(2.29)→連立方程式を行列計算で解く

連立方程式を行列計算で解く方法の方が便利です。

では導出をしていきましょう(^^)/

3点片側後退差分式(2.24)式の導出
3点片側前進差分式(2.25)の導出
4点片側後退差分式(2.28)式の導出
1. 念のためPythonで\(A\)の逆行列を求める
4点片側前進差分式(2.29)式の導出
まとめ

3点片側後退差分式(2.24)式の導出

カマキリ

まず、簡単なやつからやります。

(2.24)

\begin{align*}
f^{\prime}=\frac{f_{j-2}-4f_{j-1}+3f_{j}}{2\Delta}+\frac{\Delta^2}{3}f^{(3)}_{j}+\omicron[\Delta^3]\tag{2.24}
\end{align*}

(2.24)式が意味しているのは、以下のような図の一階微分\(\frac{df}{dx}\)を求めることです。

自身の位置\(j\)より後ろ側（\(j-1,j-2\)）の値を使って一階微分\(\frac{df}{dx}\)を表したいのです。

精度として保証できそうな次数までテーラー展開をしてすることで求めることができます。
今回は、3次の項までテーラー展開を行い、

出てきた以下の(1)式～(3)式を式変形することで、1階微分を差分で表現します。

\begin{align*}
f(x-\Delta x)=f(x)-\frac{df}{dx}\Delta x+\frac{1}{2}\frac{d^2f}{dx^2}\Delta x^2-\frac{1}{6}\frac{d^3f}{dx^3}\Delta x^3+\omicron(\Delta x^4)\tag{1}
\end{align*}

\begin{align*}
f(x-2\Delta x)=f(x)-2\frac{df}{dx}\Delta x+2\frac{d^2f}{dx^2}\Delta x^2-\frac{4}{3}\frac{d^3f}{dx^3}\Delta x^3+\omicron(\Delta x^4)\tag{2}
\end{align*}

以上で、2次の項までテーラー展開をした結果が用意できました。

ここまで来たら下記の連立方程式を解くことで「未知の値」を求められます。

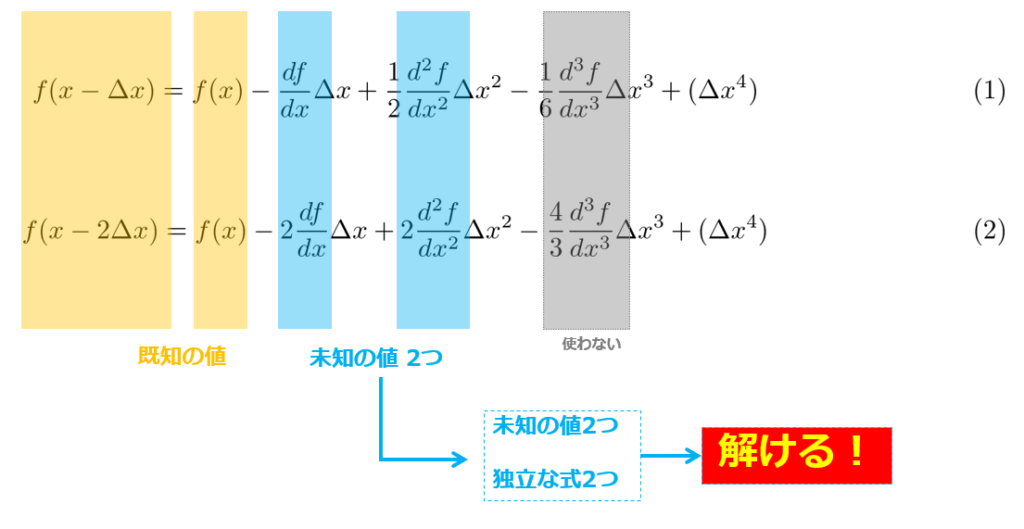
つまり、\(\frac{d f}{dx},\frac{d^2 f}{d x^2}\)を\(f(x),f(x-\Delta x), f(x-2\Delta x)\)で表せばよいという事です。

ここまで来れば(2.24)を求めるのは簡単で、\(\frac{df}{dx}\)を求めたいのですから、
(1)×4-(2)として、\(\frac{d^2 f }{dx^2}\)を消去すれば良いです。

(1)×4-(2)

\begin{align*}
4f(x-\Delta x)-f(x-2\Delta x)=3f(x)-2\frac{df}{dx}\Delta x+2\frac{d^2f}{dx^2}\Delta x^2+\frac{2}{3}\frac{d^3f}{dx^3}\Delta x^3+\omicron(\Delta x^4)
\end{align*}

よって、

\begin{align*}
\frac{df}{dx}=\frac{f(x-2\Delta x)-4f(x-\Delta x)+3f(x)}{2\Delta x}
+\frac{\Delta x^2}{3}\frac{d^3f}{dx^3}+\omicron(\Delta x^4)\tag{3}
\end{align*}

今は、\(f(x)\)が連続であるとしてテーラー展開しましたが、実際の数値計算では格子点にしか値がないため、とびとびの値をとることになります。

👆このように考えると(3)式は、

\begin{align*}
\frac{df}{dx}=\frac{f_{j-2}-4f_{j-1}+3f_{j}}{\Delta x}+\frac{\Delta x^2}{3}\frac{d^3f}{dx^3}+\omicron(\Delta x^4)\tag{4}
\end{align*}

これが(2.24)式ということになります。

\begin{align*}
f^{\prime}=\frac{f_{j-2}-4f_{j-1}+3f_{j}}{2\Delta}+\frac{\Delta^2}{3}f^{(3)}_{j}+\omicron[\Delta^3]\tag{2.24}
\end{align*}

この離散化はテーラー展開において、3次以降は無視するため2次精度の片側差分となります。

そして、自身の位置\(j\)とその後ろ側（\(j-1,j-2\)）の計3点を使っているため、これは3点式の2次精度の後退差分と呼びます。

3点片側前進差分式(2.25)の導出

(2.25)を導出するには、(2.24)と同じ導出過程をたどれば良いです。

今度は、自身の位置\(j\)より前側（\(j+1,j+2\)）の値を使って\(\frac{df}{dx}\)を表わすことを考えます。

導出過程は、読者の課題にしておきます。

☟結果は以下のようになるので、試してみてください。

(2.25)

\begin{align*}
f^{\prime}=\frac{-3f_{j}+4f_{j+1}-f_{j+2}}{2\Delta}-\frac{\Delta^2}{3}f^{(3)}_{j}+\omicron[\Delta^3]\tag{2.25}
\end{align*}

4点片側後退差分式(2.28)式の導出

カマキリ

今度は、ちょっと複雑です！

(2.28)

\begin{align*}
f^{\prime\prime}=\frac{-f_{j-3}+4f_{j-2}-5f_{j-1}+2f_{j}}{\Delta^2}+\frac{11\Delta^2}{12}f^{(4)}_{j}+\omicron[\Delta^3]\tag{2.28}
\end{align*}

(2.28)式が意味しているのは、以下のような図の二階微分\(\frac{d^2f}{dx^2}\)を求めることです。

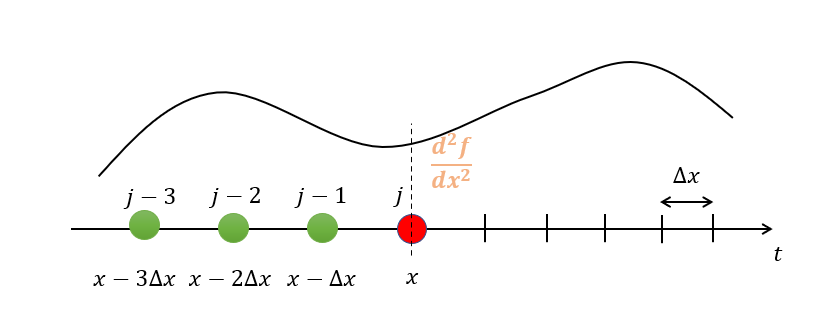
自身の位置\(j\)より後ろ側（\(j-1,j-2,j+3\)）の値を使って二階微分\(\frac{d^2f}{dx^2}\)を表したいのです。

まず、4次の項までのテーラー展開を用意します。

\begin{align*}
f=f\tag{5}
\end{align*}

\begin{align*}
f(x-\Delta x)=f(x)-\frac{df}{dx}\Delta x+\frac{1}{2}\frac{d^2f}{dx^2}\Delta x^2-\frac{1}{6}\frac{d^3f}{dx^3}\Delta x^3+\frac{1}{24}\frac{d^4f}{dx^4}\Delta x^4+\omicron(\Delta x^5)\tag{6}
\end{align*}

\begin{align*}
f(x-2\Delta x)=f(x)-2\frac{df}{dx}\Delta x+2\frac{d^2f}{dx^2}\Delta x^2-\frac{4}{3}\frac{d^3f}{dx^3}\Delta x^3+\frac{2}{3}\frac{d^4f}{dx^4}\Delta x^4+\omicron(\Delta x^5)\tag{7}
\end{align*}

\begin{align*}
f(x-3\Delta x)=f(x)-3\frac{df}{dx}\Delta x+\frac{9}{2}\frac{d^2f}{dx^2}\Delta x^2-\frac{9}{2}\frac{d^3f}{dx^3}\Delta x^3+\frac{27}{8}\frac{d^4f}{dx^4}\Delta x^4+\omicron(\Delta x^5)\tag{8}
\end{align*}

以上で、4次の項までテーラー展開をした結果が用意できました。

ここまで来たら先ほどと同様に連立方程式を解けばよいという事になります。

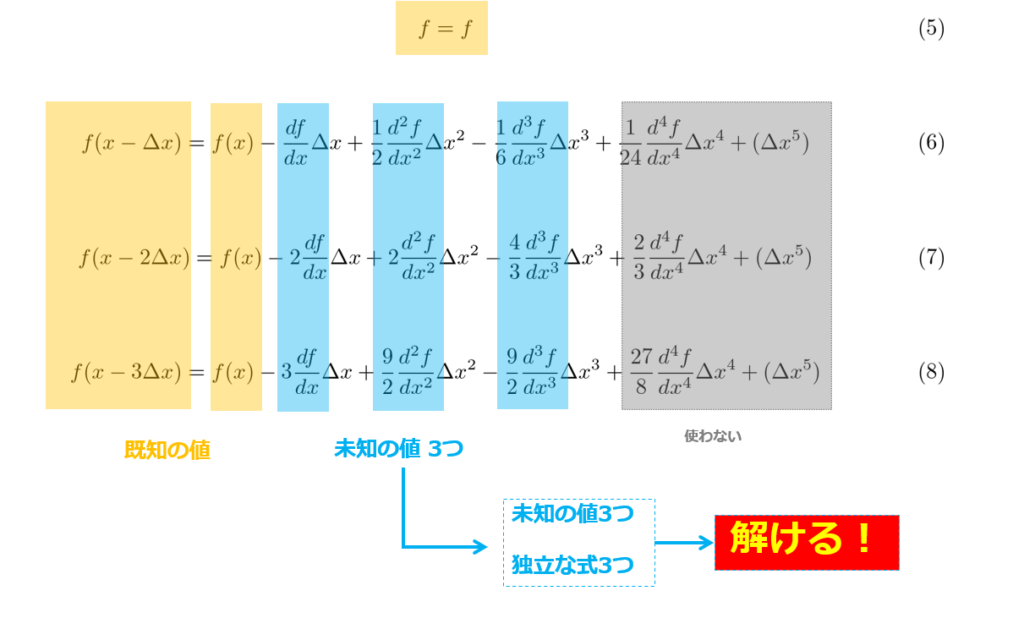
さすがにこの連立方程式を代数的に解くのはめんどうなので、行列計算で処理したいと思います。

👆こちらを行列式にまとめて・・・・

\begin{align*}
\begin{pmatrix}
f\\
f(x-\Delta x)-\frac{\Delta x^4}{24}\frac{d^4f}{dx^4}\\
f(x-2\Delta x)-\frac{2\Delta x^4}{3}\frac{d^4f}{dx^4}\\
f(x-3\Delta x)-\frac{27\Delta x^4}{8}\frac{d^4f}{dx^4}
\end{pmatrix}
=\begin{pmatrix}
1 &0 &0 &1 \\
1 &-1 &\frac{1}{2} &-\frac{1}{6} \\
1 &-2 &2 &-\frac{4}{3} \\
1 &-3 &\frac{9}{2} & \frac{9}{2}
\end{pmatrix}
\begin{pmatrix}
f\\
\frac{df}{dx}\Delta x\\
\frac{d^2f}{dx^2}\Delta x^2\\
\frac{d^3f}{dx^3}\Delta x^3
\end{pmatrix}\tag{9}
\end{align*}

さらにまとめると・・・・行列計算にすることができます。

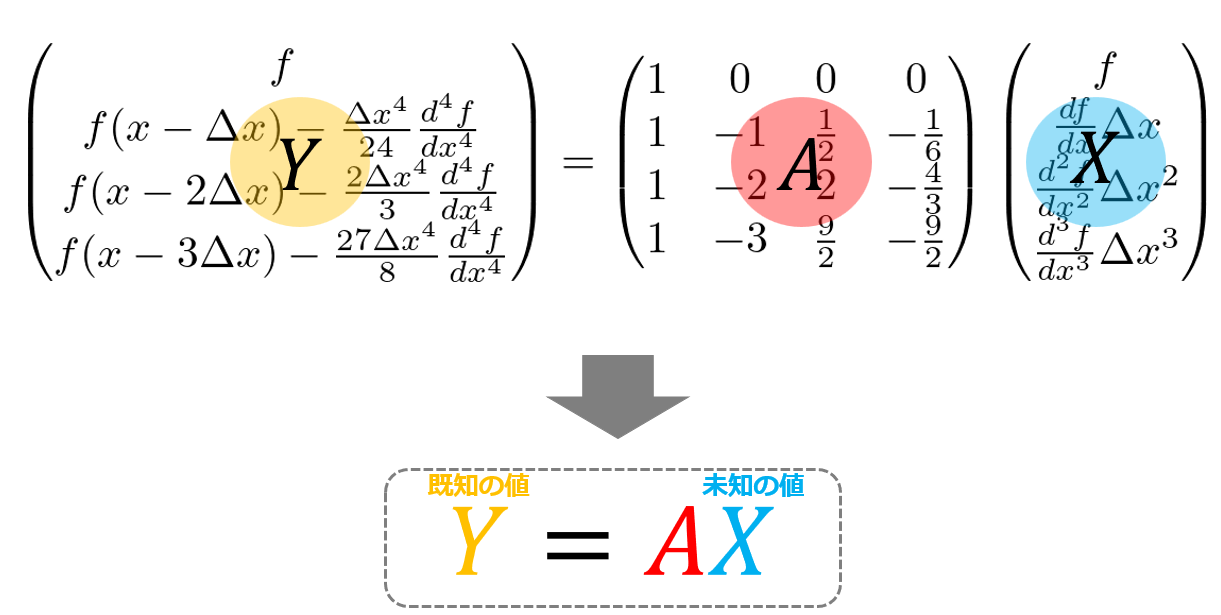
見やすさのために、右辺と左辺を逆にして・・・・

\begin{align*}
AX=Y\tag{10}
\end{align*}

行列\(X\)を求めたいので、逆行列\(A^{-1}\)を求めて(10)式の左から作用させて・・・

\begin{align*}
X=A^{-1}Y\tag{11}
\end{align*}

とすれば、行列\(X\)が求まるのがわかりますね(^^)

いったんわかりやすくするために文字で置き換えておきます。

\begin{align*}
\begin{pmatrix}
1 &0 &0 &0 \\
1 &-1 &\frac{1}{2} &-\frac{1}{6} \\
1 &-2 &2 &-\frac{4}{3} \\
1 &-3 &\frac{9}{2} &- \frac{9}{2}
\end{pmatrix}
\begin{pmatrix}
x_{1}\\
x_{2}\\
x_{3}\\
x_{4}
\end{pmatrix}
=
\begin{pmatrix}
y_{1}\\
y_{2}\\
y_{3}\\
y_{4}
\end{pmatrix}
\end{align*}

ではどうやって(11)式の\(X\)を求めるのか・・・・？？

線形代数の知識を使えばいろいろな解法がありますが、一番簡単な方法として「拡大係数行列」を使って計算していく方法です。

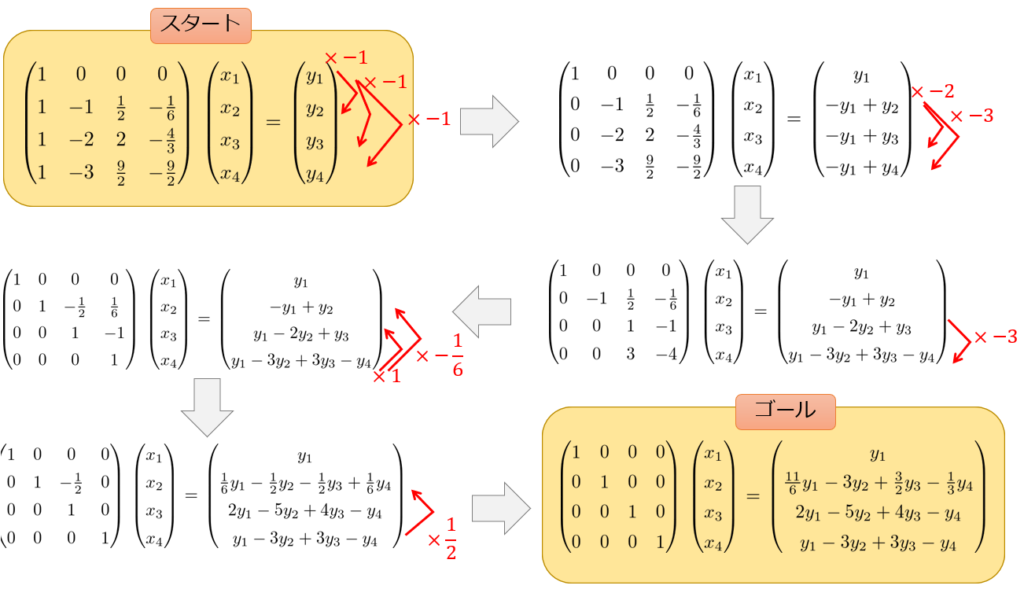
途中式はごちゃぐちゃしていますが、「スタート」と「ゴール」だけ確認できれば良いでしょう！

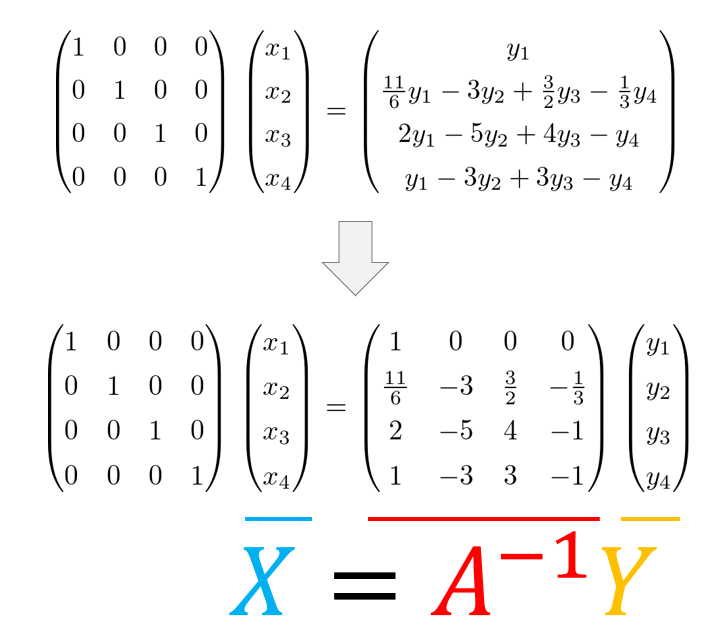
(2.24)式を導出したよりもスマートにすべての変数を求めることができていますよね。

それで・・・

とにかく今は求めたい式というのが3行目の、

\begin{align*}
x_{3}=2y_{1}-5y_{2}+4y_{3}-y_{4}\tag{12}
\end{align*}

なので、

(12)式の変数に置いた式を元に戻して・・・

\begin{align*}
\frac{d^2f}{dx^2}\Delta x^2 &=2f-5\bigg(f(x-\Delta x)-\frac{\Delta x^4}{24}\frac{d^4f}{dx^4}\bigg)\\
&+4\bigg(f(x-2\Delta x)-\frac{2\Delta x^4}{3}\frac{d^4f}{dx^4}\bigg)\\
&-\bigg(f(x-3\Delta x)-\frac{27\Delta x^4}{8}\frac{d^4f}{dx^4}\bigg)\tag{13}
\end{align*}

(13)式を整理すると・・・

\begin{align*}
\frac{d^2f}{dx^2}=\frac{2f-5f(x-\Delta x)+4f(x-2\Delta x)-f(x-3\Delta x)}{\Delta x^2}-\frac{11\Delta^2}{12}\frac{d^4f}{dx^4}\tag{14}
\end{align*}

今は、\(f(x)\)が連続であるとしてテーラー展開しましたが、実際の数値計算では格子点にしか値がないため、とびとびの値をとることになります。

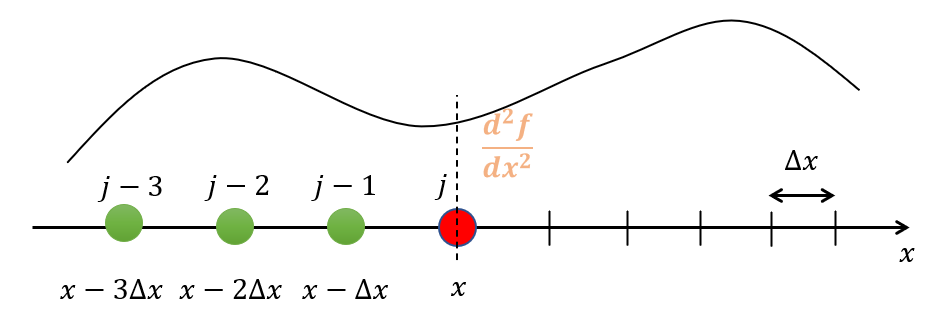
👆このように考えると(14)式は、

\begin{align*}
\frac{d^2f}{dx^2}=\frac{-f_{j-3}+4f_{j-2}-5f_{j-1}+2f_{j}}{\Delta^2}+\frac{11\Delta^2}{12}f^{(4)}_{j}+\omicron[\Delta^3]\tag{15}
\end{align*}

これが(2.28)式ということになります。

\begin{align*}
f^{\prime\prime}=\frac{-f_{j-3}+4f_{j-2}-5f_{j-1}+2f_{j}}{\Delta^2}+\frac{11\Delta^2}{12}f^{(4)}_{j}+\omicron[\Delta^3]\tag{2.28}
\end{align*}

この離散化はテーラー展開において、3次以降は無視するため2次精度の片側差分となります。

そして、自身の位置\(j\)とその後ろ側（\(j-1,j-2,j-3\)）の計4点の値を使っているため、これは4点式の2次精度の後退差分と言えるでしょう！

念のためPythonで\(A\)の逆行列を求める

(2.28)式を手計算で求めましたが、ちょっと不安なので数値計算で本当に正しいかを見ておきます。

何を確認するかですが・・・\(A\)の逆行列を確認します。

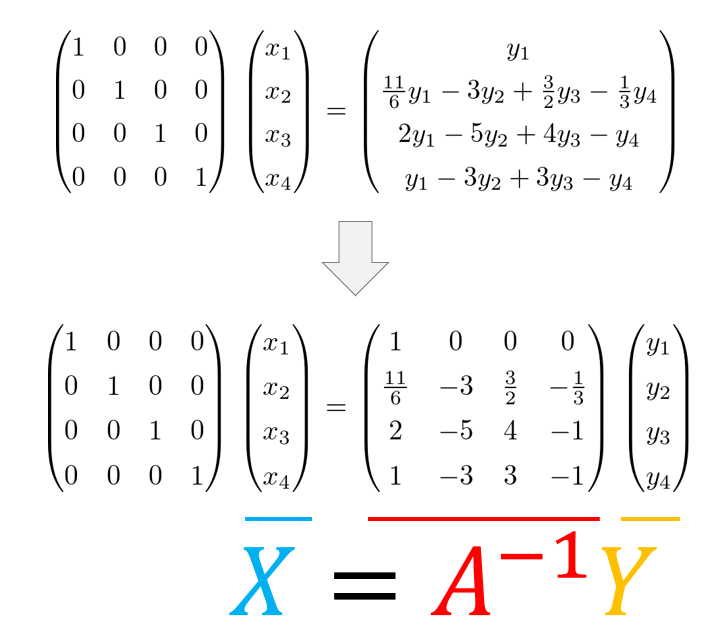
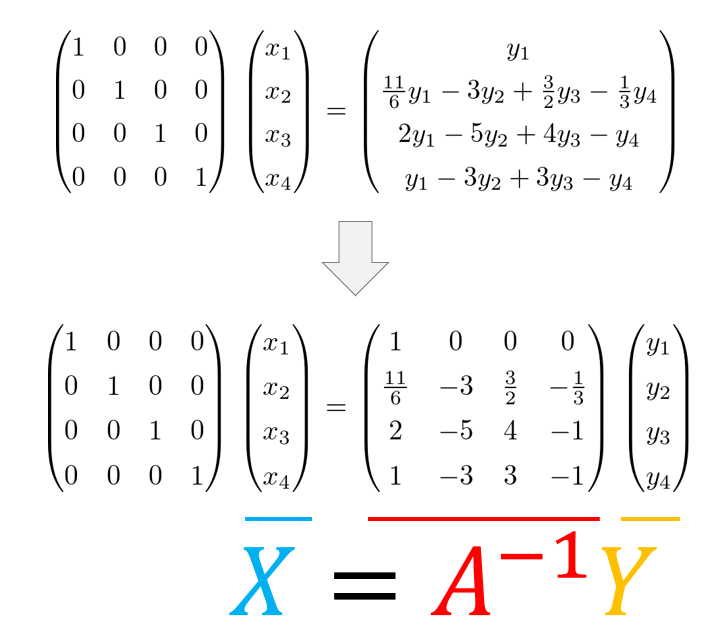
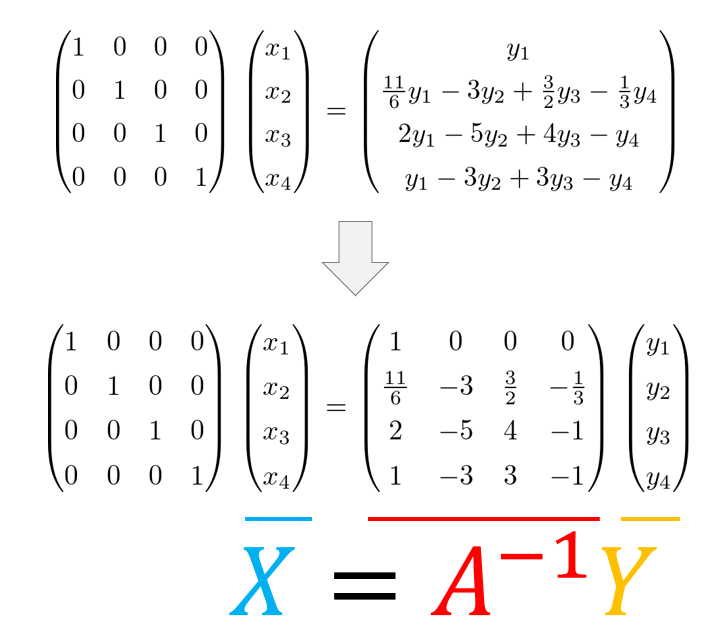
Pythonのnumpyを使えばあっという間に逆行列が計算できます。

import numpy as np

A = np.array([
              [1,0,0,0],
              [1,-1,1/2,-1/6],
              [1,-2,2,-4/3],
              [1,-3,9/2,-9/2]
])

inv_A = np.linalg.inv(A)
inv_A

import numpy as np

A = np.array([

[1,0,0,0],

[1,-1,1/2,-1/6],

[1,-2,2,-4/3],

[1,-3,9/2,-9/2]

])

inv_A = np.linalg.inv(A)

inv_A

【結果】

array([[ 1.        ,  0.        ,  0.        ,  0.        ],
       [ 1.83333333, -3.        ,  1.5       , -0.33333333],
       [ 2.        , -5.        ,  4.        , -1.        ],
       [ 1.        , -3.        ,  3.        , -1.        ]])

array([[ 1. , 0. , 0. , 0. ],

[ 1.83333333, -3. , 1.5 , -0.33333333],

[ 2. , -5. , 4. , -1. ],

[ 1. , -3. , 3. , -1. ]])

分数の部分は割り算で出てきているので、わかりにくいですが逆行列\(A^{-1}\)が手計算の結果と同じですね。

どうやら計算ミスはなさそうです。

4点片側前進差分式(2.29)式の導出

(2.29)を導出するには、(2.28)と同じ導出過程をたどれば良いです。

今度は、自身の位置\(j\)より前側（\(j+1,j+2,j+3\)）の値を使って\(\frac{d^2f}{dx^3}\)を表わすことを考えます。

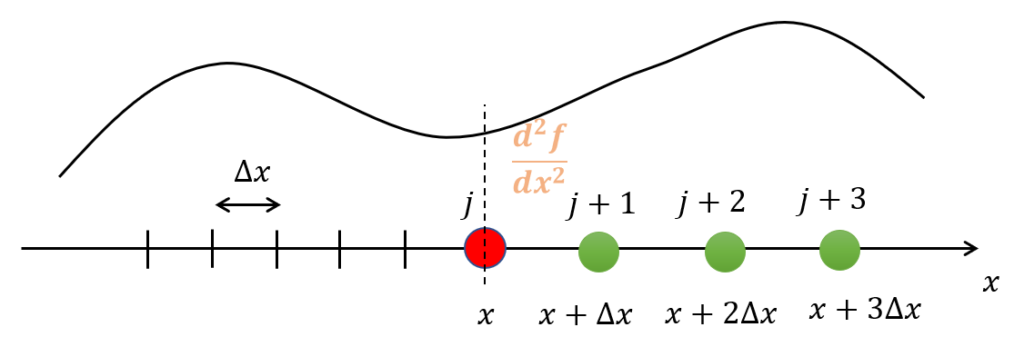
導出過程は、読者の課題にしておきます。

☟結果は以下のようになるので、試してみてください。

(2.29)

\begin{align*}
f^{\prime\prime}=\frac{2f_{j}-5f_{j+1}+4f_{j+2}-f_{j+3}}{\Delta^2}+\frac{11\Delta^2}{12}f^{(4)}_{j}+\omicron[\Delta^3]\tag{2.29}
\end{align*}

というわけで導出は以上です(^^)/

まとめ

記事の内容はこちら

「乱流の数値シミュレーション」

乱流の数値シミュレーション改訂版

梶島岳夫

4,975円(04/15 21:30時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

p.28(2.24)、(2.25)
p.29(2.28)、(2.29)

を導出する。

\(\frac{df}{dx}\)のような一階微分を、等間隔格子での片側差分でどう表されるのかという話です。
結果を示しておくと・・・

(2.24)

\begin{align*}
f^{\prime}=\frac{f_{j-2}-4f_{j-1}+3f_{j}}{2\Delta}+\frac{\Delta^2}{3}f^{(3)}_{j}+\omicron[\Delta^2]\tag{2.24}
\end{align*}

(2.25)

\begin{align*}
f^{\prime}=\frac{-3f_{j}+4f_{j+1}-f_{j+2}}{2\Delta}-\frac{\Delta^2}{3}f^{(3)}_{j}+\omicron[\Delta^2]\tag{2.25}
\end{align*}

※ここでの\(\Delta\)は、\(\Delta x\)の意味です。

p.29の(2.28),(2.29)は\(\frac{d^2 f}{dx^2}\)のような二階微分を、等間隔格子での片側差分でどう表されるのかという話です。
結果を示しておくと・・・

(2.28)

\begin{align*}
f^{\prime\prime}=\frac{-f_{j-3}+4f_{j-2}-5f_{j-1}+2f_{j}}{\Delta^2}+\frac{11\Delta^2}{12}f^{(4)}_{j}+\omicron[\Delta^3]\tag{2.28}
\end{align*}

(2.29)

\begin{align*}
f^{\prime\prime}=\frac{2f_{j}-5f_{j+1}+4f_{j+2}-f_{j+3}}{\Delta^2}+\frac{11\Delta^2}{12}f^{(4)}_{j}+\omicron[\Delta^3]\tag{2.29}
\end{align*}

\(f^{(4)}_{j}\)は\(\frac{d^4 f}{dx^4}\)の意味ですが、数値計算ではこの項は使わないので(2.28)(2.29)はテーラー展開の2次の項までしか使っていないため、2次精度の離散化です。
※ここでの\(\Delta\)は、\(\Delta x\)の意味です。

記事にして質問者さんに返答したらとても喜んでくれました(^^)/

このように、記事の書いても誰の役に立つかはわかりませんが、きっと誰かの役に立つと思って記事を書いていこうと思います_(._.)_

数値計算は偏微分方程式を離散化するがために、方程式の精度が悪くなったり、解が不安定になったりします。

色々と勉強することは多いです・・・