こんにちは(@t_kun_kamakiri)(‘◇’)ゞ
本内容は、「比熱の温度依存性の理解のため」のための記事です。
シリーズ化していますので「なぜ比熱に温度依存性があるのか?」を知りたい方は、以下のシリーズを読んで頂ければ理解できると思います。
量子力学における基礎式であるシュレディンガー方程式を使うことになります(^^)/
2原子の分子のシュレディンガー方程式を極座標表記にして解く
本記事を読むにあたって詳細の計算まで踏み込んで議論していては、時間がかかりすぎるため前提にしている知識が3つあります。
必要とする前提知識
- 古典力学
- 統計力学(平衡)
- じゃっかんの量子力学の知識
前回の復習:2原子分子のシュレディンガー方程式
前回の記事では、2原子分子のシュレディンガー方程式を記述し、2原子の重心運動と重心周りの相対運動に方程式を分解しました。
2原子分子のハミルトニアン演算子\(\hat{H}\)に対して、
\hat{H} &=\hat{H}_{M}+\hat{H}_{re}\\
&=-\frac{\hbar^2}{2M}\nabla_{\boldsymbol{R}}^2-\frac{\hbar^2}{2\mu}\nabla_{\boldsymbol{r}}^2+V(r)\tag{7}
\end{align*}
は、
\Phi=\psi_{M}(\boldsymbol{R})\phi_{re}(\boldsymbol{r})
\end{align*}
と変数分離できる解を持ちます。
シュレディンガー方程式を「重心運動」と「重心周りの相対運動」に分離させたものが以下の2式です。
結果は以下です(‘◇’)ゞ
「重心運動に依るハミルトニアン」量子力学的取り扱い
-\frac{\hbar^2}{2M}\nabla_{\boldsymbol{R}}^2\psi_{M}(\boldsymbol{R}) = E_{R}\psi_{M}(\boldsymbol{R}) \tag{1}
\end{align*}
「重心周りの相対運動のハミルトニアン」量子力学的取り扱い
\bigg(-\frac{\hbar^2}{2\mu}\nabla_{\boldsymbol{r}}^2+V(r)\bigg)\phi_{re}(\boldsymbol{r}) = E_{re}\phi_{re}(\boldsymbol{r})\tag{2}
\end{align*}
こうすると、全エネルギーを「重心の並進運動エネルギー固有値」と「重心周りのエネルギー固有値」に分けることができます。
\underset{全エネルギー}{\underline{E}}=\underset{重心の並進運動エネルギー固有値}{\underline{E_M}}+\underset{重心周りのエネルギー固有値}{\underline{E_{re}}}
\end{align*}
(1)式はシュレディンガー方程式の基礎中の基礎「自由粒子(ポテンシャルが無い状態)」での偏微分方程式なので、これ以上いじりようがないですが、
(2)式は球対称なポテンシャル\(V(r)\)中でのシュレディンガー方程式ですので、デカルト表記ではなく極座標で扱うのが上手い解析の方法です。
ちなみに、こちらの記事でも重心周りの運動に関しては、極座表示に変換してから比熱を計算しました。興味がある方は是非読んでください。
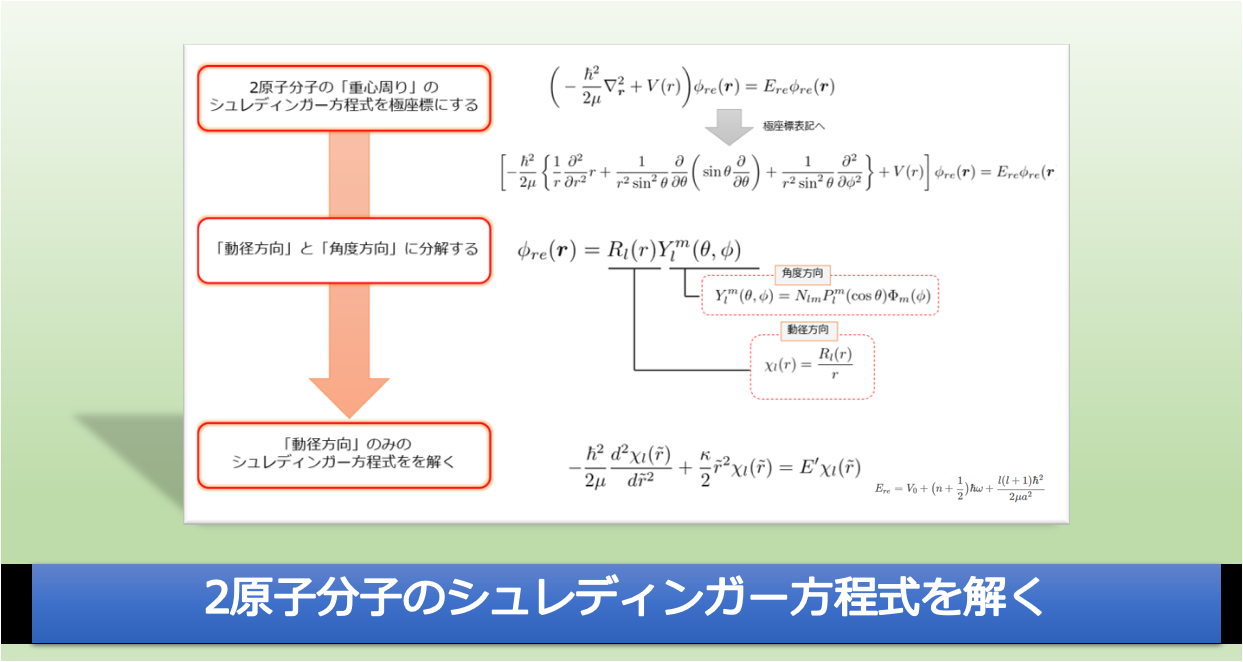
(2)式を解く方法と、その流れさえつかんでいれば良いと考えて「解き方フロー」を以下のようにまとめておきました。
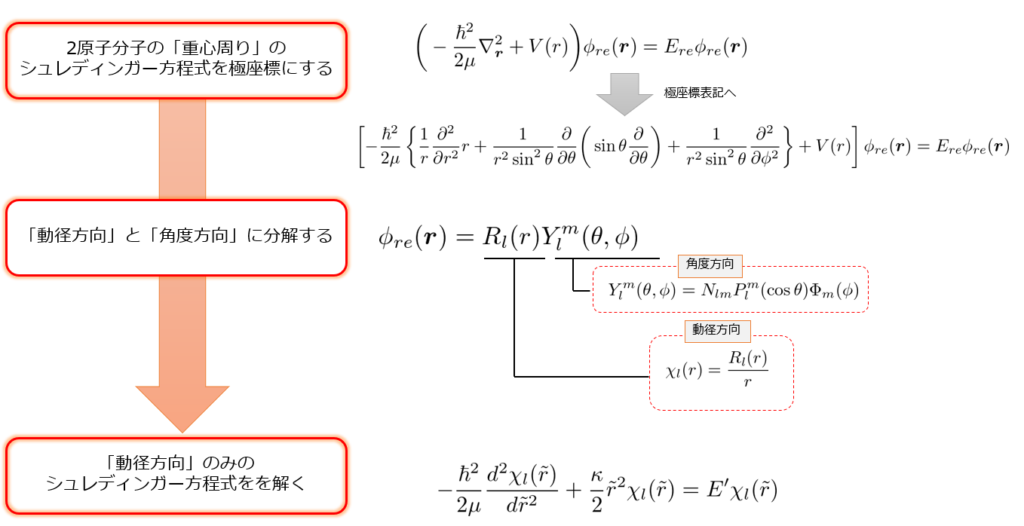

これにより、一度学んだことがある人やこれから学ぶ人でも迷子になることなく、且つ目的を失うことなく読んでいけると思います。
球対称なポテンシャル中のシュレディンガー方程式は極座標で扱おう
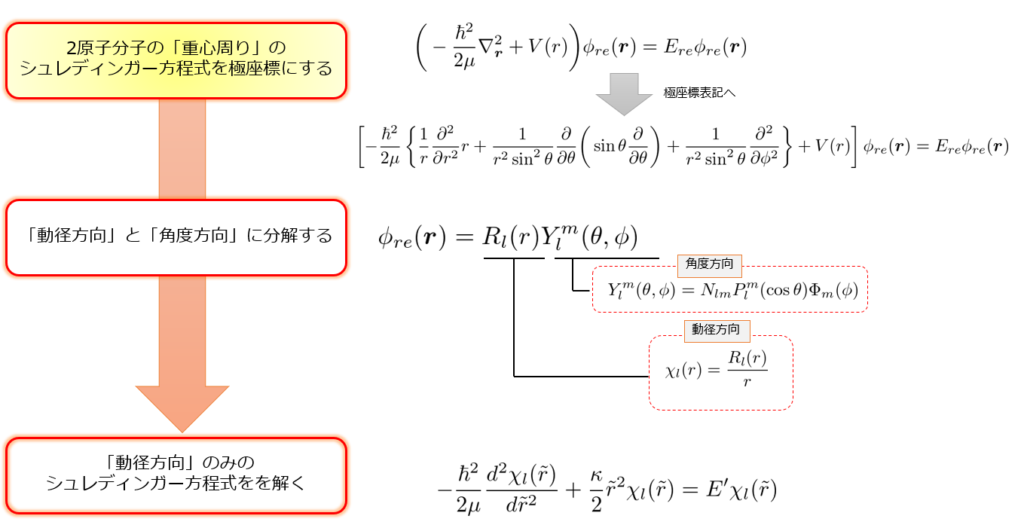

「重心周りの相対運動のハミルトニアン」量子力学的取り扱い
\bigg(-\frac{\hbar^2}{2\mu}\nabla_{\boldsymbol{r}}^2+V(r)\bigg)\phi_{re}(\boldsymbol{r}) = E_{re}\phi_{re}(\boldsymbol{r})\tag{2}
\end{align*}
やっかいなのは、\(\nabla\)(ナブラ演算子)ですよね。
ラプラシアンの極座標表記
ラプラシアンの極座標の導出はかなり複雑になるのですが、こちらの記事を丁寧に読めば理解ができます。
今回は、結果だけ使うことにしましょう。
\Delta =\frac{1}{r}\frac{\partial^2 }{\partial r^2}r+\frac{1}{r^2\sin^2\theta}\frac{\partial }{\partial \theta}\bigg(\sin\theta\frac{\partial}{\partial\theta}\bigg)+\frac{1}{r^2\sin^2\theta}\frac{\partial^2}{\partial\phi^2}\tag{3}
\end{align*}
(3)式を(2)式に使ってやるわけです。
\left [ -\frac{\hbar^2}{2\mu}
\left \{ \frac{1}{r}\frac{\partial^2 }{\partial r^2}r+\frac{1}{r^2\sin^2\theta}\frac{\partial }{\partial \theta}\bigg(\sin\theta\frac{\partial}{\partial\theta}\bigg)+\frac{1}{r^2\sin^2\theta}\frac{\partial^2}{\partial\phi^2}\right \} +V(r) \right ]\phi_{re}(\boldsymbol{r})= E_{re}\phi_{re}(\boldsymbol{r})\tag{4}
\end{align*}
極座標でのシュレディンガー方程式を動径方向と角度方向に分解する
(4)式は一見複雑すぎて解析的には解けないような気がしてなりませんが、解析的に解く方法が用意されています。
詳しくは「猪木河合の量子力学Ⅰ」がとってもお勧めです。
ハミルトニアン演算子も、動径方向と角度方向に分解することができるのですよね。
そうは言っても(4)式をどう解くかという問題には変わりありません。
\left [ -\frac{\hbar^2}{2\mu}
\left \{ \frac{1}{r}\frac{\partial^2 }{\partial r^2}r+\frac{1}{r^2\sin^2\theta}\frac{\partial }{\partial \theta}\bigg(\sin\theta\frac{\partial}{\partial\theta}\bigg)+\frac{1}{r^2\sin^2\theta}\frac{\partial^2}{\partial\phi^2}\right \} +V(r) \right ]\phi_{re}(\boldsymbol{r})= E_{re}\phi_{re}(\boldsymbol{r})\tag{4}
\end{align*}
これを解く方法は、多くの参考書やネット情報で解説がされていますので、ここでわざわざ詳細を話すことはしません。
極座標表記のシュレディンガー方程式を解く
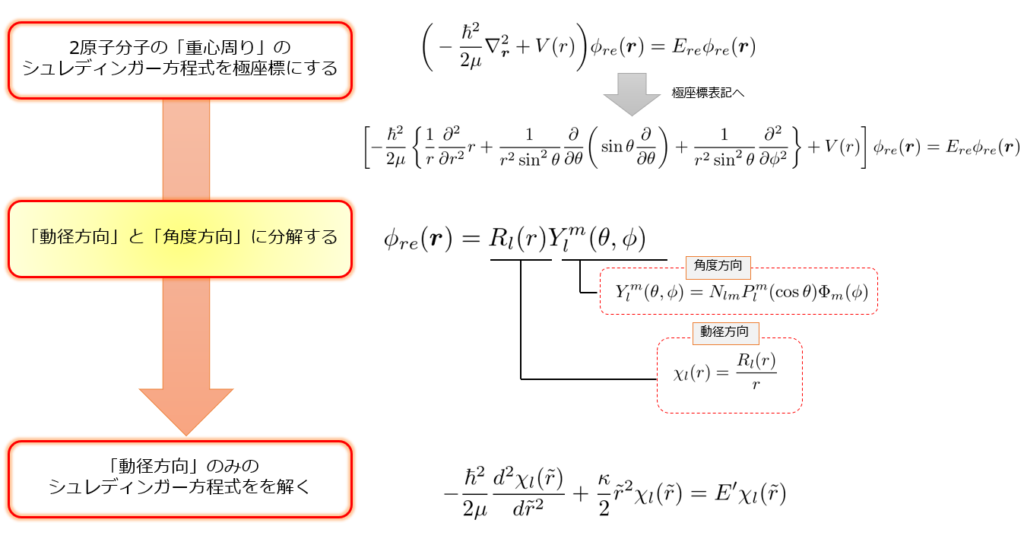

これを解く上手い方法は「動径方向」と「角度方向」に分離して解く方法です。
「動径方向」と「角度方向」に分離
波動関数(固有値問題なので固有関数ともいう)を、
\phi_{re}(\boldsymbol{r})=\underset{動径方向}{\underline{R(r)}}\underset{動径方向}{\underline{Y(\theta,\phi)}}\tag{5}
\end{align*}
と書くことでシュレディンガー方程式自体を「動径方向」と「角度方向」に分離できます。
角度成分もさらに分離
Y^{m}_{l}(\theta,\phi)=N_{lm}P^{m}_{l}(\cos\theta)\Phi_{m}(\phi)
\end{align*}
\(Y^{m}_{l}(\theta,\phi)\):球面調和関数
\(P^{m}_{l}(\cos\theta)\):ルジャンドルの倍関数
(6)式を使うことで、(4)式のシュレディンガー方程式は動径方向だけにできます。
動径方向のシュレディンガー方程式を近似的に解く
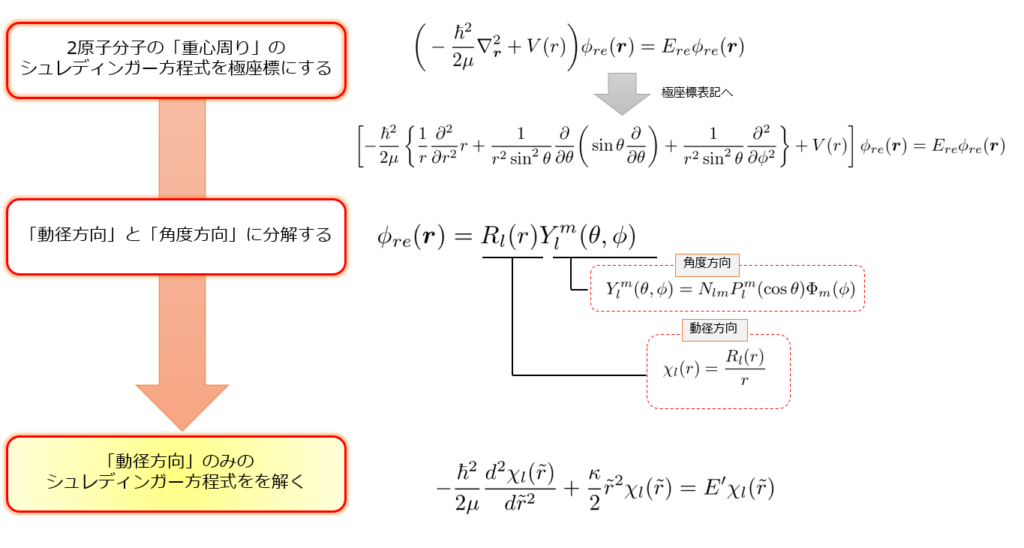

-\frac{\hbar^2}{2\mu}\frac{d^2\chi_{l}(r)}{dr^2}+\bigg(V(r)+\underset{角運動量の固有値より}{\underline{\frac{l(l+1)\hbar^2}{2\mu r^2}}}\bigg)\chi_{l}(r)=E_{re}\chi_{l}(r)
\end{align*}
これを解くのは非常にやっかいです。
しかし、2原子分子の場合はある距離\(a\)で保った状態で存在しているはずです。
つまり、\(r=a\)でポテンシャル\(V(r)\)は極小値を取っていると考えても良いはずです。
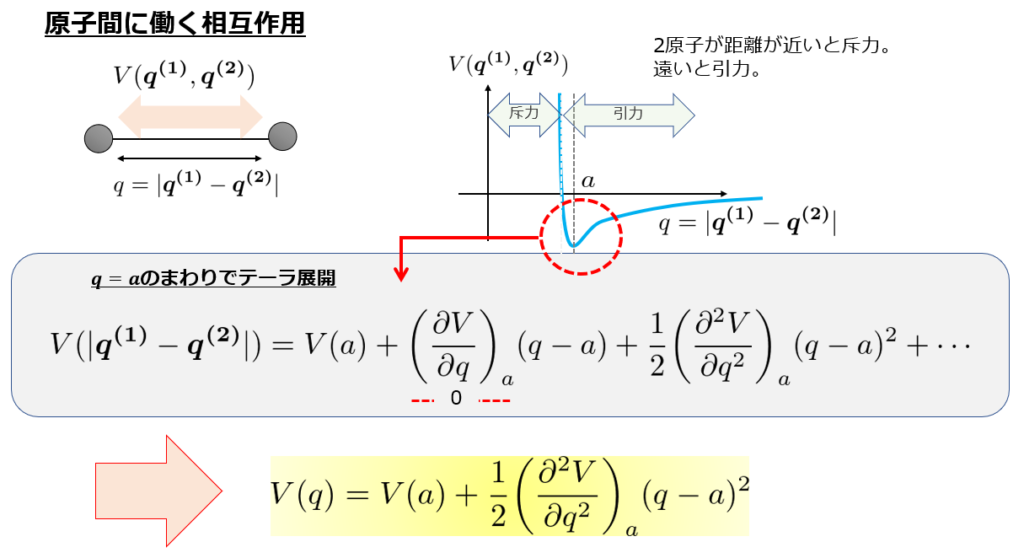

※絵は一般座標\(q\)としていますが、今の場合は\(r=q\)です。
そして、角運動量の固有値から来ていた項は\(r=a\)での現象を扱っていると考えて、\(\frac{l(l+1)\hbar^2}{2\mu a^2}\)としてやります。
ポテンシャルが\(V(r)=V_0+\frac{\kappa}{2}(r-a)^2\)という形に近似できるので、
-\frac{\hbar^2}{2\mu}\frac{d^2\chi_{l}(r)}{dr^2}+\bigg(V_0+\frac{\kappa}{2}(r-a)^2+\underset{角運動量の固有値より}{\underline{\frac{l(l+1)\hbar^2}{2\mu a^2}}}\bigg)\chi_{l}(r)=E_{re}\chi_{l}(r)\tag{7}
\end{align*}
となります。
\(\tilde{r}=r-a\)と置きます。
-\frac{\hbar^2}{2\mu}\frac{d^2\chi_{l}(\tilde{r})}{d\tilde{r}^2}+\bigg(\frac{\kappa}{2}\tilde{r}^2+\underset{角運動量の固有値より}{\underline{\frac{l(l+1)\hbar^2}{2\mu a^2}}}\bigg)\chi_{l}(\tilde{r})=E_{re}\chi_{l}(\tilde{r})\tag{8}
\end{align*}
\(\frac{l(l+1)\hbar^2}{2\mu a^2}\)が定数だということがわかるので、\({E}’=E_{re}-\frac{l(l+1)\hbar^2}{2\mu a^2}\)と置いておくと、
-\frac{\hbar^2}{2\mu}\frac{d^2\chi_{l}(\tilde{r})}{d\tilde{r}^2}+\frac{\kappa}{2}\tilde{r}^2\chi_{l}(\tilde{r})={E}’\chi_{l}(\tilde{r})\tag{9}
\end{align*}
ポテンシャルが調和振動子の1次元シュレディンガー方程式に帰着しました。
- 1次元ポテンシャルは縮退無し
- 1次元調和振動子ポテンシャルによるエネルギー固有値は\({E}’=\big(n+\frac{1}{2}\big)\hbar\omega\)
※\(\omega=\sqrt{\frac{\kappa}{\mu}}\)
ということは、(4)式のエネルギー固有値は近似的には、
E_{re}=V_0+\big(n+\frac{1}{2}\big)\hbar\omega+\frac{l(l+1)\hbar^2}{2\mu a^2}\tag{10}
\end{align*}
となります。
これで「重心周りの運動に対するエネルギー固有値」を近似的に求めることができました。
まとめ
今回は、2原子分子のシュレディンガー方程式の固有値を近似的ではありますが求めることができました。
再度「解く方のフロー」と結果を示します。
【解き方のフロー】
\left [ -\frac{\hbar^2}{2\mu}
\left \{ \frac{1}{r}\frac{\partial^2 }{\partial r^2}r+\frac{1}{r^2\sin^2\theta}\frac{\partial }{\partial \theta}\bigg(\sin\theta\frac{\partial}{\partial\theta}\bigg)+\frac{1}{r^2\sin^2\theta}\frac{\partial^2}{\partial\phi^2}\right \} +V(r) \right ]\phi_{re}(\boldsymbol{r})= E_{re}\phi_{re}(\boldsymbol{r})\tag{4}
\end{align*}
のエネルギー固有値は、
E_{re}=V_0+\big(n+\frac{1}{2}\big)\hbar\omega+\frac{l(l+1)\hbar^2}{2\mu a^2}\tag{10}
\end{align*}
お勧めの参考書
本記事の内容の「シュレディンガー方程式」を解く問題は以下の問題集に詳しく書かれているので興味のある方は持っておくことをお勧めします。
豊富な問題が揃っているので、大学の講義のレポートなどにはとても役に立つと思います。