こんにちは(@t_kun_kamakiri)。
2020年7月頃から一ヶ月ほど、物理の質問サービスをしています。
特に多かった質問として、以下の微分方程式の解法に関する質問です。
ひとつが、↓これ。
もうひとつが、↓これ。
この2つの微分方程式の解法についての質問が結構ありました。
僕が学生時代にもこの手の問題というのは、理解に苦しみました。
なぜなら、大学に入ってはじめて触れる微分方程式というものだからです。
(1)の解法が理解できたら、(2)の解法に進むという形で勉強を進めれば良いと思います。
微分方程式、
- (1)の物理的な意味は何かを理解する
- (1)の微分方程式の解法を理解する
- 微分方程式を解いた解の振る舞いを理解する
こちらの3点を詳しく解説します。
(2)の解法はまた別途記事をアップします。
では、さっそくやっていきましょう!
ダンパーの運動方程式
今回考えるのは以下のような問題です。
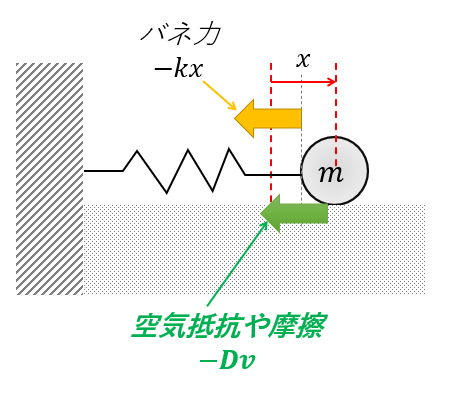
バネにつながれた質量\(m\)の質点が、速度に比例する抵抗(空気抵抗や摩擦)を受けている場合の運動方程式です。
\(x\)は自然長からのバネの伸びです。
運動方程式
となります。
そして、これを以下のように整理します。
※\(\dot{x}=\frac{dx(t)}{dt}\)
※\(\ddot{x}=\frac{d^2x(t)}{dt^2}\)
本日、解く微分方程式は(3)です。
2階斉次線形微分方程式とは何か
まず、与えられた微分方程式の名前の意味を説明しておきます。
別に覚える必要はないですが、名前を覚えておいた方が解法の理解にもつながります。
今回解くべき微分方程式は、「2階斉次線形微分方程式」と呼ばれているものです。
それぞれの用語の説明を以下にしておきます。

2階の微分方程式なので、積分を2回して得られる\(x(t)\)には必ず任意の積分定数が2つ付きます。
※ここ重要です。
以下で出てくる\(A,B\)などが積分定数です。
2階斉次線形微分方程式の解法
では、これから(3)の微分方程式を解きます。
解き方は定石というのがあります。
次の4点を意識して解きます。
- $x(t)=Ae^{\lambda t}$の形を仮定して(3)に代入⇒\(\lambda\)の値を決める。
※\(A\):任意定数 - 積分定数が2つ付いた解が得られます(「一般解」と呼ばれます。)
※「一般解」については後ほど説明 - \(\lambda\)の条件によって解の振る舞いを場合分け
- 任意の2つの積分定数は、初期条件などから決まる。
任意定数がない解を「特殊解」と呼びます。
「なんで、\(x(t)=Ae^{\lambda t}\)の解を想定するの?」って思うかもしれませんが、後に分かります。
では、順番にやっていきましょう!
\(x(t)=Ae^{\lambda t}\)の形を仮定して(3)に代入⇒\(\lambda\)の値を決める。
(3)式の一般解を\(x(t)=Ae^{\lambda t}\)と置き、(3)式に代入して以下の特性方程式より\(\lambda\)を決める。
目的は一言で言うと「\(\lambda\)」を決めることです。
では、\(x(t)=Ae^{\lambda t}\)を1階微分、2階微分してみましょう。
- \(\frac{dx}{dt}=\lambda Ae^{\lambda t}\)
- \(\frac{d^2x}{dt^2}=\lambda^2 Ae^{\lambda t}\)
以上の計算で気づくように、解として\(x(t)=Ae^{\lambda t}\)という形を仮定すると、何回も\(e^{\lambda t}\)が出てきて扱いやすいんですよね。
それが、\(x(t)=Ae^{\lambda t}\)の形の解を仮定する理由です。
実際に、代入すると以下となります。
ここで、\(Ae^{\lambda t}\neq 0\)なので両辺で割ってしまいます。
そうすると以下のような2次方程式が出てきます。
この2次方程式はサクッと解を書くと、
\lambda=-\gamma\pm\sqrt{\gamma^2-\omega_{0}^2}\tag{6}
\end{align*}
となります。
積分定数が2つ付いた解が得られます(「一般解」と呼ばれます。)
積分定数を2つ使って、2階斉次線形微分方程式の一般解を書き下す。
(6)式から、2つの\(\lambda\)が出てきたのがわかりますね。
- \(\lambda_{1}=-\gamma+\sqrt{\gamma^2-\omega_{0}^2}\)
- \(\lambda_{2}=-\gamma-\sqrt{\gamma^2-\omega_{0}^2}\)
ということで、この2つの\(\lambda\)を使うと、(3)の一般解は以下のようになります。
x(t)=A e^{(-\gamma+\sqrt{\gamma^2-\omega_{0}^2})t}+B e^{(-\gamma-\sqrt{\gamma^2-\omega_{0}^2})t}\tag{7}
\end{align*}
先ほども触れましたが、2階微分があるため積分を2階することになり、積分定数が2つ付きます。
このように任意定数(積分定数)がつく状態の解のことを一般解と呼びます。
(7)が本当に(3)の解になっているのか不安な方は、(7)の積分定数を含んだまま(3)の左辺に代入してみてください。
ちゃんとゼロになりますから。
しかし、まだ(3)の解の振る舞いは決定していません。
λの条件によって解の振る舞いを場合分け
ここが、この問題の一番めんどくさいところです。
しかし、大学一年生の力学初学者がよくつまづくところですので丁寧に解説したいと思います!
1.\(\gamma=0\)のとき
簡単なやつからいきましょう!
ひとつめとして「\(\gamma=0\)のとき」です。
これは、「減衰項無しの単振動」の振る舞いをする解のことです。
これはどういう状況かと言うと、\(\gamma=\frac{D}{2m}=0\)なので、速度に比例する抵抗がない状況のことです。
運動方程式
↑こちらを解いているのと同じです。
(8)を解いても良いですが、(7)で解が求まっているので\(\gamma=0\)としましょう!
x(t)=A e^{i\omega_{0}\, t}+B e^{-i\omega_{0} \,t}\tag{9}
\end{align*}
このままの形でも良いですが、(9)は、オイラーの公式「\(e^{i\theta}=\cos\theta+i\sin\theta\)」を用いると、「sin, cos」の波の形で記述できます。
x(t)&=A \big(\cos \omega_{0} t+i\sin \omega_{0} t\big)+B \big(\cos \omega_{0} t-i\sin \omega_{0} t\big)\\
&=(A+B)\cos\omega_{0}t +i(A-B)\sin\omega_{0}t \\
&=A^{\prime}\cos\omega_{0} t +B^{\prime}\sin\omega_{0}t
\end{align*}
最後に、\(A^{\prime}=A+B\)、\(B^{\prime}=i(A+B)\)と新たに定数を定義しなおすことで以下となります。
(10)が(8)の一般解ということです。
元の運動方程式からわかるように、解の振る舞いは、バネ力を復元力とした振動運動ということですね!
2.\(0<\gamma<\omega_{0}\)のとき
では、次の条件に行きましょう!
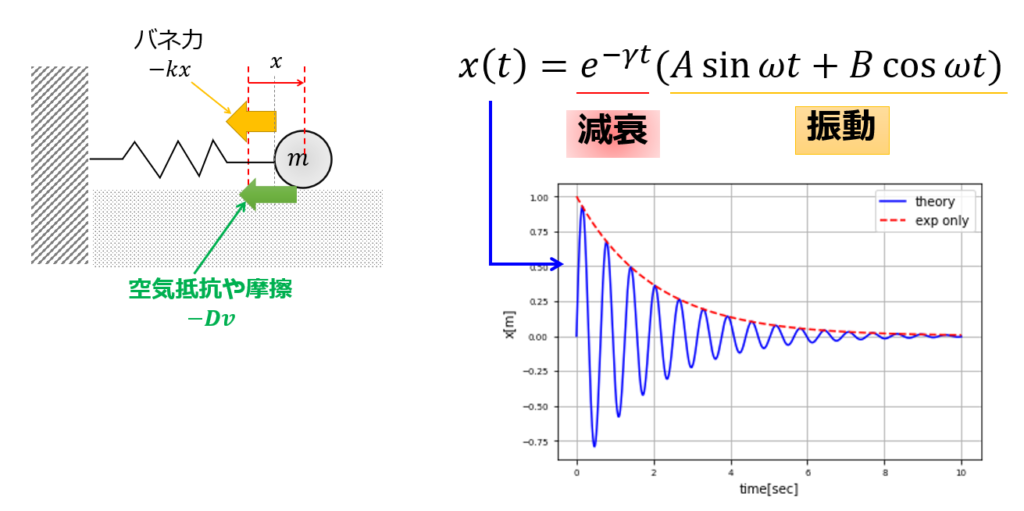
今度は、「減衰振動」と呼ばれる解の振る舞いについてです。
減衰振動とは、「1.減衰項無しの単振動」とは違い、振動しながら振動が減衰していく解のことです。
\(\lambda\)のルートがある項の中身が虚数になってしまいます。
⇒\(\sqrt{\gamma^2-\omega_{0}^2}\)が虚数
なので、実数\(\omega=\sqrt{\omega_{0}^2-\gamma^2}\)を使って\(\lambda\)を以下のように書きます。
\lambda&=-\gamma\pm\sqrt{\gamma^2-\omega_{0}^2}\\
&=-\gamma\pm i\omega \tag{11}
\end{align*}
(11)にすると解(7)が以下のようになります。
x(t)=A e^{(-\gamma+i\omega )t}+B e^{(-\gamma-i\omega )t}\tag{12}
\end{align*}
これも、オイラーの公式「\(e^{i\theta}=\cos\theta+i\sin\theta\)」を用いると、「sin, cos」の波の形で記述できます。
x(t)&=A e^{-\gamma \,t}\big(\cos \omega t+i\sin \omega t\big)+B e^{-\gamma \,t}\big(\cos \omega t-i\sin \omega t\big)\\
&=e^{-\gamma \,t}\bigg((A+B)\cos\omega t +i(A-B)\sin\omega t \bigg)\\
&=e^{-\gamma \,t}\bigg(A^{\prime}\cos\omega t +B^{\prime}\sin\omega t \bigg)
\end{align*}
最後に、\(A^{\prime}=A+B\)、\(B^{\prime}=i(A+B)\)と新たに定数を定義しなおすことで以下となります。
(12)が「\(0<\gamma<\omega_0\)」における一般解ということです。

3.\(\gamma>\omega_{0}\)のとき
では、次の条件に行きましょう!
今度は、「過減衰」と呼ばれる解の振る舞いについてです。
先ほどまでは、「単振動」の要素が強かったのですが、\(\gamma\)が大きいという事は、抵抗がものすごく大きいことを意味しています。
なので、解の振る舞いには単振動の要素が無く解が減衰していく一方となります。
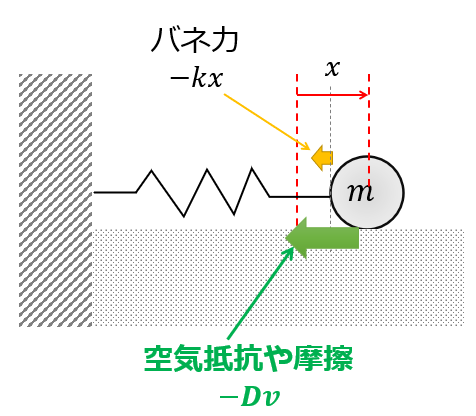

\(\lambda\)についてもう一度見ておきましょう。
- \(\lambda_{1}=-\gamma+\sqrt{\gamma^2-\omega_{0}^2}\)
- \(\lambda_{2}=-\gamma-\sqrt{\gamma^2-\omega_{0}^2}\)
\(\gamma >\sqrt{\gamma^2-\omega_{0}^2}\)なので、この2つともに負の実数であることがわかりますよね。
x(t)=A e^{(-\gamma+\sqrt{\gamma^2-\omega_{0}^2})t}+B e^{(-\gamma+\sqrt{\gamma^2-\omega_{0}^2})t}\tag{7}
\end{align*}
こちらは指数部分が負となるため、以下のように時間とともに減衰していく解となります。
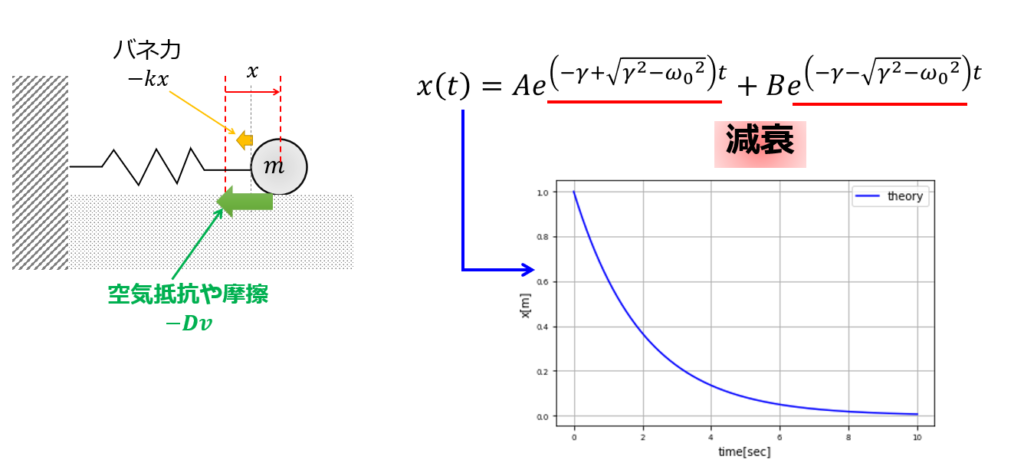

以下のようにあえて文字でわかりやすく置き換えておきますかね。
- \(\lambda_{1}=-\gamma+\sqrt{\gamma^2-\omega_{0}^2}=-a<0\)
- \(\lambda_{2}=-\gamma-\sqrt{\gamma^2-\omega_{0}^2}=-b<0\)
そうすると、
(13)が「\(\gamma>\omega_0\)」における一般解ということです。
では、最後の条件にいきます。
4.\(\gamma=\omega_{0}\)のとき
このときはやっかいで、\(\lambda\)の値が1つしか出てきません。
- \(\lambda_{1}=\lambda_{2}=-\gamma\)
\(\lambda\)は、このひとつだけしかないのですよね。
そうなると、2階の微分方程式は2つの積分定数を使って、一般解を書くというのができなくなりました。
そこで、\(\lambda=-\gamma\)なので、一般解は\(e^{-\gamma t}\)の形を持っていることだけはわかったとして、先ほどまで定数として扱っていた定数と思い切って\(A(t)\)をとしてやります。
x(t)=A(t)e^{-\gamma t}\tag{14}
\end{align*}
これを(3)を満たすような\(A(t)\)を見出せばよいのではないかという事になります
- \(\dot{x}=\dot{A}(t)e^{-\gamma t}-A(t)\gamma e^{-\gamma t}\)
- \(\ddot{x}=\ddot{A}(t)e^{-\gamma t}-2\dot{A}(t)\gamma e^{-\gamma t} +A(t)\gamma^2 e^{-\gamma t}\)
これらを(3)に代入して式を整理すると、
\bigg(\ddot{A}(t)+(2\lambda+2\gamma)\dot{A}(t)+(\lambda^2+2\gamma \lambda +\omega_{0}^{2})\bigg)e^{-\gamma t}=0\tag{15}
\end{align*}
ここで、第三項は\((\lambda^2+2\gamma \lambda +\omega_{0}^{2}=0\))であるし、第二項は\(\lambda=-\gamma\)です。しかも、\(e^{-\gamma t}\neq 0\)であることに注意すると、残るのは以下の部分だけです。
\ddot{A}(t)=0
\end{align*}
では、これを2回積分すると、
A(t)=At+B\tag{16}
\end{align*}
※\(A,B\)は任意の積分定数
となるので、積分定数が2つ付いた形ができました。
なので、今回の「\(\gamma=\omega_{0}\)」での一般解は、以下となります。
わかりにくい解になりましたが、グラフにすると以下のようになります。
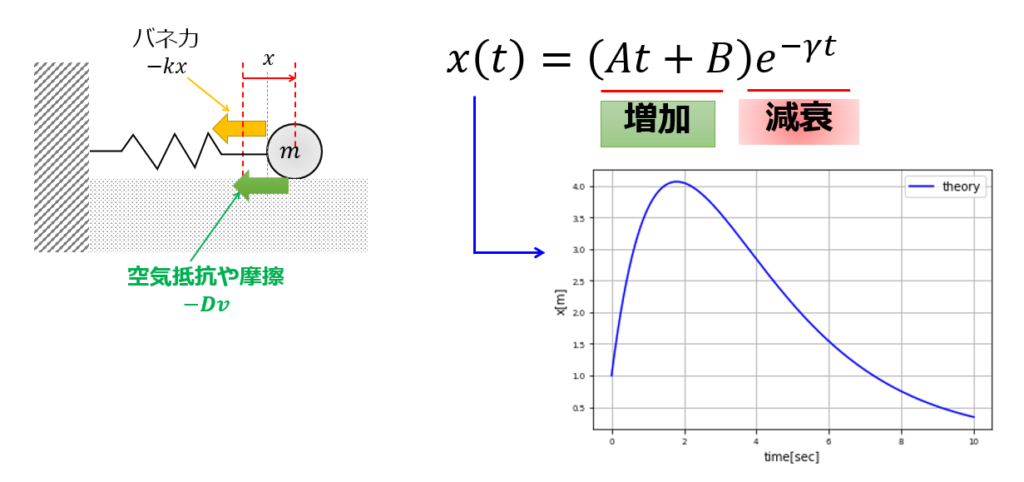
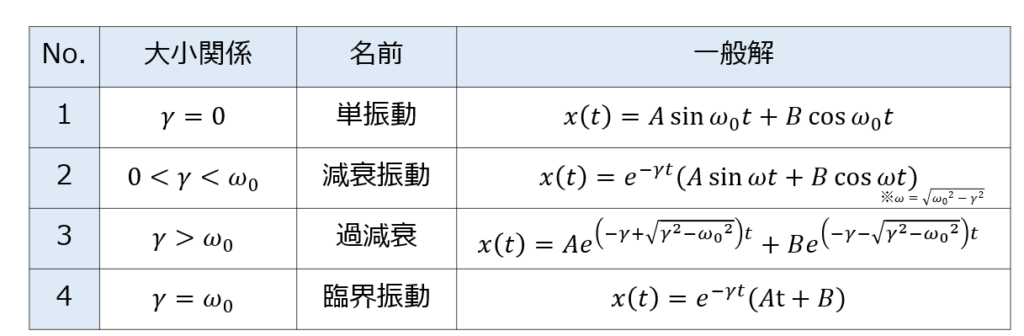
2階斉次線形微分方程式の一般解まとめ
以上のように、2階斉次線形微分方程式の解に対するまとめを記しておきます。
4.特殊解を求める
以上までの内容で、任意の2つの積分定数を使って一般解を求めましたが、任意定数が残ったままですと、解の振る舞いを決定することができませんよね。
ここでやるのは、この任意定数を決めることです。そのような解の事を特殊解と呼びます。
では、どうやって任意定数を決めるかというと、だいたい初期条件から決定することが多いです。
【ここでの目的】初期条件から、2つの任意定数を決定する。
では、初期条件を以下であるとして、2つの任意定数を決めましょう。
- \(x(0)=x_{0}\)
- \(\frac{dx(0)}{dt}=v_{0}\)
初期位置と初速度を決めたという事ですね。
このように、初期条件を決めると、あとは運動方程式に従って運動することになり、解の振る舞い振る舞いは決定されるということになります。
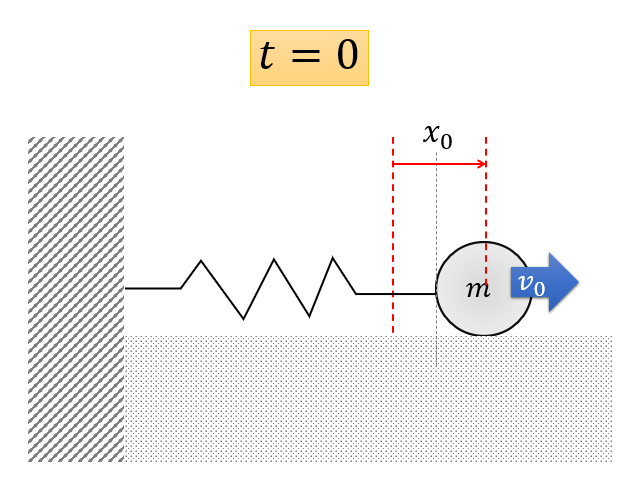

2つの定数を決定するのに2つの条件を課すことになるので、\(A,B\)は決定することができますよね。
計算過程は読者に任せるとして、結果だけ書いておきます。


※答えが間違ってたら教えてください_(._.)_
まとめ
今回は「2階斉次線形微分方程式」の解法について解説をしました。
手順を以下にまとめておきます。
おまけ:空気抵抗は本当に速度に比例するのか
本記事の内容で、速度に比例する項を「空気抵抗」と呼びましたが、実は空気抵抗は速度に比例するものではありません。
空気抵抗がどのように速度に依存するかは、正確には流れによるという事です。
ここでは、簡単にまとめておきましょう!
- 層流状態➡抵抗は速度に比例
- 乱流状態➡抵抗は速度の2乗に比例
おすすめの参考書
大学一年生がはじめて力学を学ぶときに、高校物理と大学物理の難易度のギャップに戸惑う人も多いでしょう。
ここで、紹介するのは高校物理と大学物理を埋めてくれるわかりやすい参考書ですので、どうしれもつまづいて先に進めないという方は是非読んでみてください。
高校数学と物理を教えている予備校講師陣のわかりやすい参考書と演習書を読めば大学物理の触りはOKです。
難易度として同じくらいの以下の参考書もお勧めです。